對圓錐曲線一共性之推廣

魏子賀

(河北省樂亭第一中學高三年級 063600)

設圓錐曲線的一個焦點為F,相應準線l交焦點所在的對稱軸(圖(1)中的x軸)于點M,過F的直線交圓錐曲線于A,B兩點.則MF是∠AMB的角平分線(特別地當圓錐曲線為雙曲線時,要滿足A,B兩點落在雙曲線的同一支.否則落在左右兩支上時∠AMF,∠BMF互補).

“性質”的成立必須在F為焦點且M為相應準線與對稱軸的交點的條件下(這一性質是2018年高考全國卷一19題第2問的證明，所以此處不再證明),如果改變這一條件,僅讓這兩點存在某種特定的內在聯系,我們可得到如下一組推論.

推論1 已知拋物線y2=2px(p>0)過定點F′(m,0)(m≠0)的直線交拋物線于A,B兩點,則對稱軸上存在定點M′(-m,0)使得下面結論成立：(1)當m>0時,∠AM′F′=∠BM′F′；(2)當m<0時,∠AM′F′+∠BM′F′=180°.

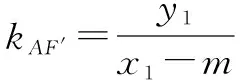
當m>0時結合圖(2)可得∠AM′F′=∠BM′F′;當m<0時結合圖(3)可得∠AM′F′+∠BM′F′=180°.若AB的斜率不存在,則必須滿足m>0,此時命題成立.

類似的結論在橢圓和雙曲線中仍然成立,見下面推論2,推論3.

證明當AB的斜率存在時(斜率不存在時成立，略去不證),設A(x1,y1),B(x2,y2),AB所在直線方程為y=k(x-m)(k≠0),將其代入橢圓方程并整理得(b2+a2k2)x2-2ma2k2x+(a2k2m2-a2b2)=0.

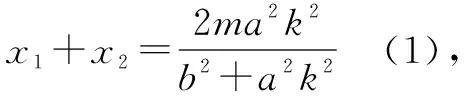
推論3的證明與推論1、2思路類似，在此不在給出.以上通過對2018年全國卷一解析幾何解答題的分析給出了三個相關推論，希望對讀者以后的學習有所幫助.