三角函數單調性問題釋疑

彭向陽

單調性是函數的一個重要性質，對三角函數而言亦然．但許多同學在解三角函數的單調性問題時，經常忽視一些基本要求．

例函數的單調遞減區間為________．

解析對于這一類自變量前的系數是負數的三角函數單調區間的求解問題，一般我們的解法是將負系數利用誘導公式變成正系數．

問題有同學質疑，為什么直接做不行呢？一定要將系數化為正嗎？那么我們先看看直接做是怎么做的．同學們的解法是：

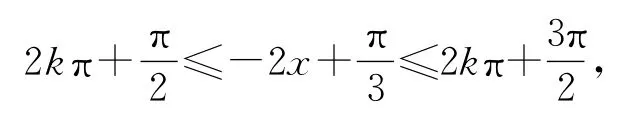
為什么得到的結果不同呢？

因為直接做就變成了復合函數的單調性問題，就必須利用復合函數的單調性——同增異減來處理．

注意：這里由于k∈Z，所以k和－k是一回事，為了簡潔，將－k用k替代．

同學們以后在解變量系數為負的三角函數單調性問題時，一定要注意先利用誘導公式化系數為正．