由一道函數題的錯解引發的探索和思考

毛雨萱

一、問題與背景

在復習導數在函數與方程中的應用時，老師給我們布置了這樣一道習題：

已知函數f（x）＝kx，，求方程f（x）＝g（x）在區間內解的個數．

這道題求解的方法我們都很明確：利用導數工具畫出函數的圖象，利用圖象數形結合求解．但是，在具體操作時，不同的處理方法，得出了大相徑庭的結果，一時間我們都感到有點奇怪和不解．

二、思路與解法

我的解題思路是參變分離：

由 方程f（x）＝g（x），得

于是，h（x）在上單調遞增，在上單調遞減，且于是由圖1得：

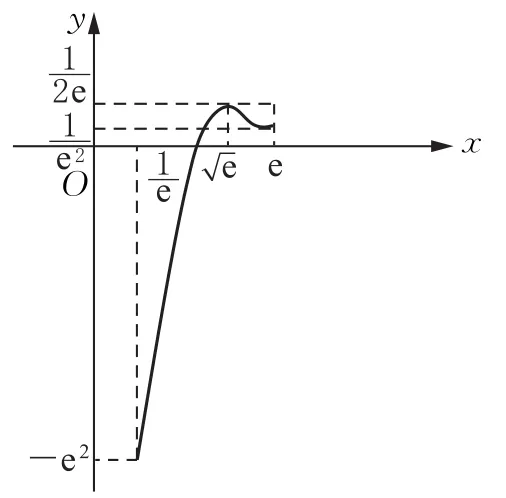
圖1

同學的思路也是參變分離：

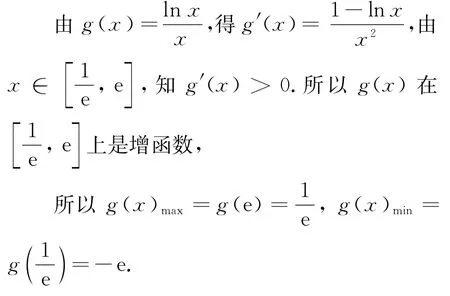
函數g（x）在上的近似圖象如圖2所示，

于是直線OA斜率直線OB斜率kOB＝－e2，

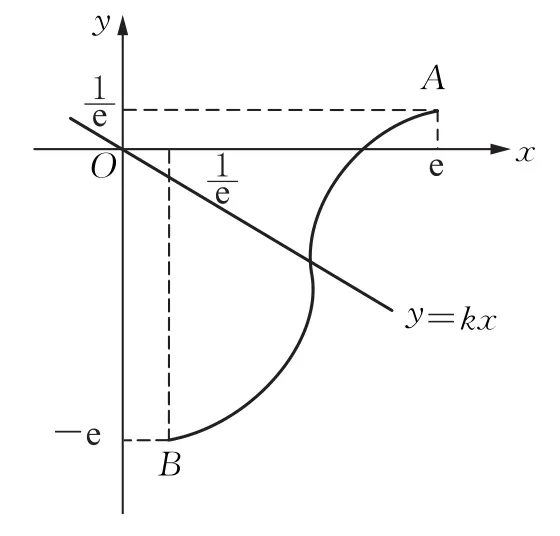
圖2

三、質疑與探索

我和同學的解法都是將方程的根轉化為兩個函數的圖象的交點來判斷，這是求解有關函數零點個數（方程解的個數）問題的通法，看起來都有理有據，但結果卻迥然不同，孰對孰錯？錯在哪里呢？

我和同學們展開探究和討論．我的解法是將問題轉化為函數y＝k與的圖象的交點個數來判斷．水平直線y＝k與的圖象的交點，根據的單調性，容易結合圖象作出判斷，我的解法應該是正確的．而同學的解法是斜線f（x）＝kx與的圖象的交點僅根據的單調性是不夠的，必須更精確地畫圖以表現出此函數的基本性態，我懷疑他的圖象不準確，故而借助MathPac軟件模擬了圖象，如圖3．

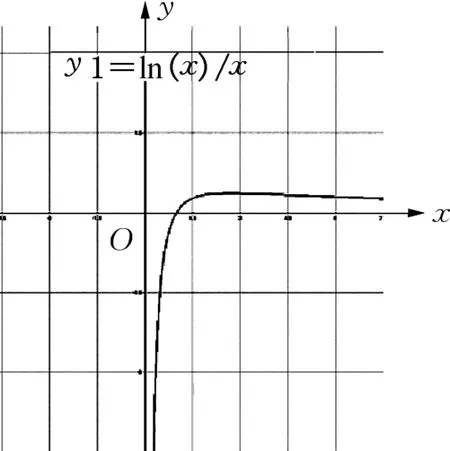
圖3

果然是由于g（x）的圖象不準確，解題時誤以為是k的最大值，忽視了在A點左側會因曲線向上彎曲（上凸），且曲率較大時，直線y＝kx過A點時會和曲線g（x）有另一個交點（在A點左側），此時k的最大值應在與曲線相切時取得．

經過查閱資料和對問題的探究找到問題的根源，由同學的解法知在上是增函數，又，當時在上是上凸函數，于是我們可以作出g（x）的更精確的圖象如圖4，函數f（x）＝kx與的圖象在在內有相切的情況．

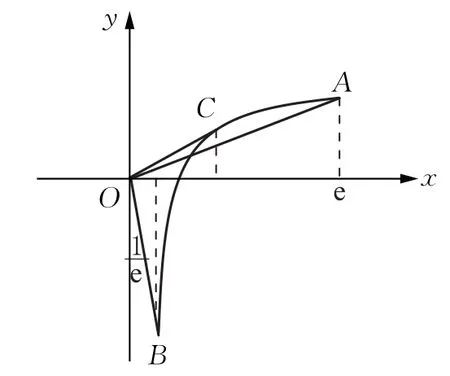
圖4

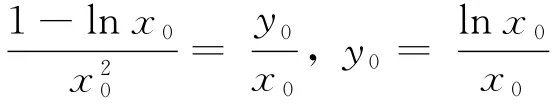
通過分析，除了我和同學的解法之外，還獲得了一種得到全班都認可的解法，同時也解釋了上述剖析的正確性和上述錯解的根源．

令f（x）＝g（x），即即kx2＝lnx，在同一個坐標系中畫出函數y＝kx2和函數的圖象，如圖5．函數y＝kx2隨著k增大，圖象從開口方向向下，逐漸變化為一條直線（k＝0），再變化為開口向上，在開口向上時開口逐漸減小．因此，圖象在從開口向下逐漸變化的過程中，首先經過點此時k＝－e2，然后變化為一條直線y＝0，此時k＝0，當k＞0時函數y＝kx2的圖象逐漸變化到經過點（e，1），此時與函數的圖象有兩個交點，然后變化到與函數y＝lnx的圖象只有一個交點（相切），此時，求解過程如下：

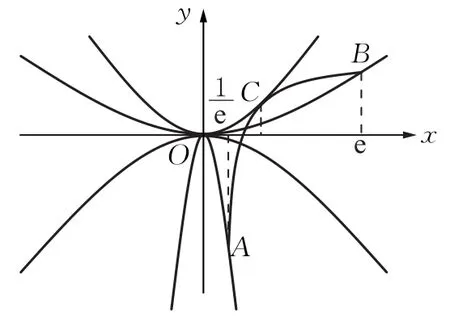
圖5

當k＜－e2時方程無解，當－e2≤k＜時方程有一解，當時方程有兩解，當時方程有一解，當時方程無解．

四、思考和感悟

從三種解法的探究和分析來看，盡管處理的方法類似，由于方法一轉化成的兩個函數中有一個是平行于x軸的直線，所以更容易操作，后兩種方法對圖形的要求則更高；同學解法的錯誤原因在于“圖形”的不準確，因為作圖太隨意，沒有把握住圖形的基本特征和關鍵點，所以作出的圖象不能準確地反映出函數的基本形態，再加上簡單處理，想當然地得出答案，這樣錯誤的發生就不足為奇了；“數缺形時少直觀，形缺數時難入微．”我們在利用數形結合思想解題時要先從數的角度研究出函數的各項性質，再畫出函數準確的圖象，這樣才能真正將數與形完美結合起來為我們所用．