對2018江蘇高考解幾壓軸題的探究

江蘇省灌南高級中學 (222500)

劉鑫鈞 宋予林

本文就2018年江蘇省高考解析幾何壓軸題及母題的背景及共性分析，實現一般模型的提煉，通過一般模型不斷改變、變更條件，更換問題及整合關聯等過程性變式從不同角度，不同層次深化認識高考試題的本質，提升學生的探索精神與創新意識，從而培養學生的核心素養．

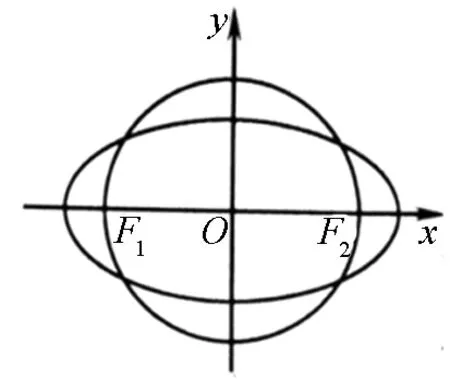
圖1

一、試題再現

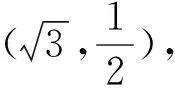
(2)設直線l與圓O相切于第一象限內的點P．①若直線l與橢圓C有且只有一個公共點，求點P的坐標；

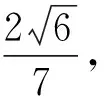
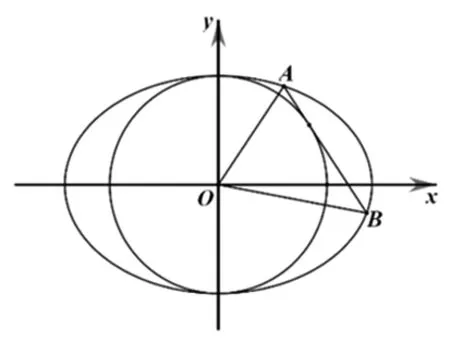
圖2

二、背景及共性分析

(一)背景：此題是如下一道常見的母題改編而來.

(1)求橢圓C的標準方程；

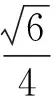
(二)共性分析

母題與高考題的共性主要有以下四個方面：

1.第二問的大前提一致：都是直線l與圓相切于第一象限；

2.條件一致：都是直線與橢圓交于A,B兩點；

3.題型一致：均是已知ΔOAB的面積值，求直線l的方程；

4.解法一致：第一問略.

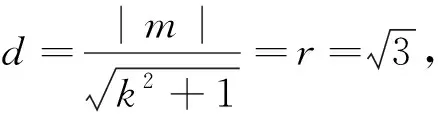
母題解法：僅僅是r,a,b在數值上有所不同，兩題在AB,d,SΔAOB計算過程完全一致.

三、試題挖掘

(一)通性通法

橢圓是高考的重點和難點，在橢圓的教學中，不能僅僅停留在一題一法的研究上，更要將一類問題的思想方法提煉出來，即通性通法的研究.

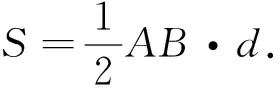
(二)擴展研究

1.模型提煉

普通高中數學課程標準(實驗)》(以下簡稱《標準》)提出，要培養學生數學抽象的核心素養，即學生能從事物的具體背景中抽象出一般規律和結構，并用數學語言予以表征.

顯然.高考題與母題中，橢圓與圓的中心均是原點，直線與圓相切，并與橢圓相交，則橢圓與圓的位置關系主要有以下三種關系：相交，內切，內含，分別如下圖所示.記這三種圖分別為圖Ⅰ、圖Ⅱ、圖Ⅲ.這三種圖形代表著三種不同的模型，這樣我們發現高考題的背景就是圖Ⅰ、而母題就是圖Ⅱ.

這樣用圖形語言進行表征，以簡馭繁，把握這類題型的本質，抽象出高度概括、表達準確、結論一般的三種模型.

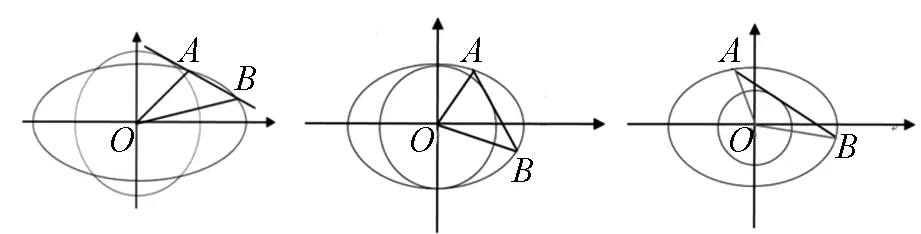
圖Ⅰ 圖Ⅱ 圖Ⅲ

2.過程性變式

《標準》要求，改變過分強調知識灌輸的傾向，將過程與方法的學習作為數學課程的重要目標，強調在學習過程中領悟與體驗，那么在平常的解題教學中如何落實呢？變式教學是有效落實目標的一種有效方式.

顧泠沅等學者把變式教學分為概念性變式和過程性變式教學兩類.概念性變式教學突出對概念內涵的理解，過程性變式教學突出對概念外延的應用，注重知識之間的聯系和拓展，通過過程性變式教學，使數學教學有層次地遞進[1].利用過程性變式可以對一個初始問題進行變式，從而深化對這類問題的認識.

⑴改變元素

①改變r的大小

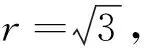
②改變面積

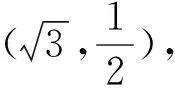
設直線l與圓O相切于第一象限內的點P．直線l與橢圓C交于A,B兩點，求SΔAOB的范圍.

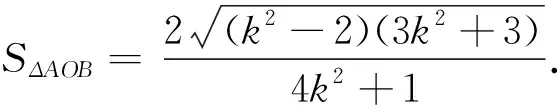
③改變r與面積

改變r的大小，由模型Ⅰ變為模型Ⅱ或模型Ⅲ，條件中由給定面積值求直線方程改為，求面積取最大值時，求直線l的方程.

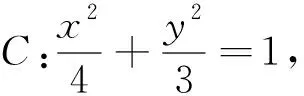
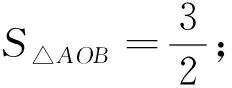
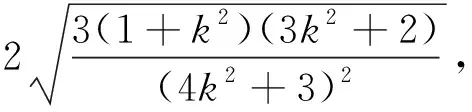
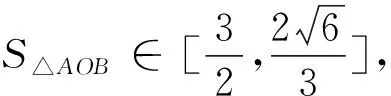
⑵變更條件

變更條件是指通過添加或去除、替換等方式改變初始問題的某些條件，而探索原結論或相關結論的變化情況的方式，從而實現從多角度，多層面深度認識問題的本質.

①變更面積條件為弦長條件

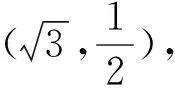
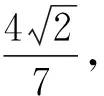
⑶更換問題

更換問題是指：背景大致相同，在初始條件不變或稍加改變之下，提出新的結論，探索新的問題.譬如高考題中橢圓與圓的位置關系是圖Ⅰ，可以改為圖Ⅱ位置關系，計算面積值改為求AB最值或范圍問題，得到變式5.

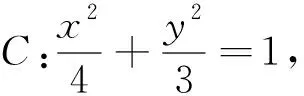
⑷整合關聯

整合關聯是指:在直線與圓相切背景不變下，改變條件或在改變元素的基礎上，把條件之間的關系或結構進行改造，研究相關問題或結論的方式.比如以圖Ⅲ為背景，已知直線方程過某一點，求S△AOB的值并探究OA,OB之間關系得到變式6.在圖Ⅲ的背景下，探求交點到切點距離與交點到焦點距離乘積的范圍，增加條件提出其它問題得到變式7.

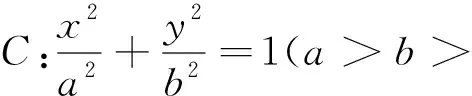
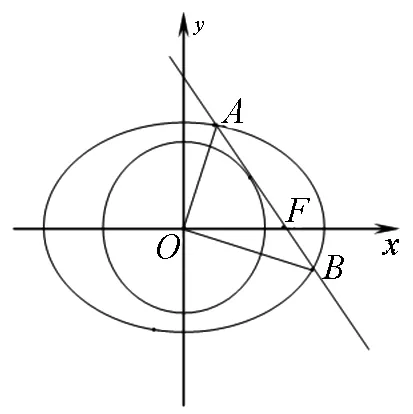
圖3

(1)求橢圓C的方程；

(2)設直線l與圓O：x2+y2=2相切，與橢圓C相交于A，B兩點．

①若直線l過橢圓C的右焦點F，求△AOB的面積；

②求證：OA⊥OB．

圖4

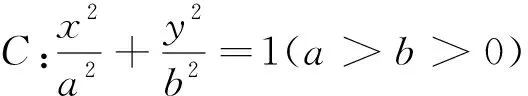
(1)求橢圓C的方程；(2)求PM·PF的取值范圍；(3)若OP⊥OQ，求點Q的縱坐標t的值.

四、結束語

G·波利亞有句名言：“發現問題比解決問題更重要”.在高三數學教學中，試題難度大，容量多，數學問題的解決僅僅完成了一半，更重要的一半在于對解題后的回顧、反思.如何發現不同試題，特別是培養學生發現高考題與我們練習題之間的區別、共性比僅僅解決問題更重要，能提煉出一般的模型，即培養學生數學抽象能力，在過程性變式教學中培養學生邏輯推理、數學運算的能力，有效地提高學生的數學核心素養.