帶馬爾科夫利率的雙險種復合雙二項離散風險模型破產概率研究
,
(山東科技大學 數學與系統科學學院,山東 青島 266590)
Lundberg提出經典風險模型之后,在保險精算領域,眾多學者對經典風險模型進行改進和推廣,使其更符合保險公司經營現狀。文獻[1]最早將保費收取過程推廣為復合二項模型,將保費收取過程離散化,給出關于破產概率及盈余在破產前及破產瞬間的聯合分布的若干結果。隨后,中外學者對復合二項風險模型進行了大量研究。文獻[2]將索賠過程推廣為復合二項模型。文獻[3]用復合二項模型的破產概率來近似經典連續時間復合泊松模型的破產概率,討論了具有幾何索賠量的復合二項模型的相關結果。文獻[4]將保費收取過程與索賠過程同時推廣為復合二項過程。文獻[5-6]利用生成函數推導出復合二項風險模型的破產概率。此外,隨著金融市場的發展,保險公司可用資金擴張且行業競爭激烈,使保險公司對外投資具有了可能性及必要性。文獻[7]最早引入馬爾科夫鏈利率,用遞推方程歸納法給出了有限時間的破產概率上界。文獻[8-10]在此基礎上,對考慮投資情況的破產模型進行了進一步研究。文獻[11]考慮離散情況下,將期初保費收取進行短期投資,得到新模型的破產概率。文獻[12]在考慮通貨膨脹率等隨機因素干擾的情況下,將盈余資本進行投資并推廣得到新的雙二項風險模型。文獻[13]考慮帶有常利率及相依結構的風險過程,并在此基礎上研究破產概率。文獻[14-17]在離散時間下引入馬爾科夫鏈利率,對風險模型的破產概率進行進一步研究。本研究在已有文獻的基礎上,引入第二個險種,將單一險種的風險模型推廣為多險種的風險模型,將經典風險模型改進為雙險種復合雙二項風險模型,采用馬爾科夫鏈利率預期未來收益,利用全概率公式等數學工具得到破產概率積分表達式,運用鞅方法得到破產概率上界。
1 模型的描述
考慮帶馬爾科夫鏈利率的離散時間雙險種復合雙二項風險模型:
(1)
其中,Un為保險公司在n時刻的盈余。對于險種Ⅰ,每單位時間內發生理賠的概率為p1,不發生理賠的概率為q1。用{εn}n≥1表示險種Ⅰ第n個單位時間內的理賠發生情況,即P(εn=1)=p1,P(εn=0)=q1。理賠額{Xn}n≥1是取正值的獨立同分布于X的隨機變量,其中X的分布函數FX(x)=P(X≤x)。類似地,對于險種Ⅱ,每單位時間內發生理賠的概率為p2,不發生理賠的概率為q2。用{ξn}n≥1表示險種Ⅱ第n個單位時間內的理賠發生情況,即P(ξn=1)=p2,P(ξn=0)=q2。理賠額{Yn}n≥1是取正值的獨立同分布于Y的隨機變量,其中Y的分布函數FY(x)=P(Y≤y)。初始盈余為u,每單位時間內保費收取情況隨機,時刻n是否收取保費用δn表示,保費收取發生概率為p3,不發生的概率為q3,即P(δn=1)=p3,P(δn=0)=q3,保費收取率為c。
設利率{In,n=0,1,2,…}是一個馬爾科夫鏈。對所有的n=0,1,2,…,In可以取任意的一個可能值i0,i1,…,iN,這些可能值構成一個集合,稱為馬爾科夫鏈{In,n=0,1,2,…}的狀態空間,用I={i0,i1,…,iN}來表示。則對所有的n=0,1,2,…和所有的狀態is,it,…,itn-1,有
P(In+1=it|In=is,In-1=itn-1,…,I0=it0)=P(In+1=it|In=is)=pst≥0 ,
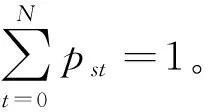
定義破產時刻T=inf{n:n>0,Un<0|U0=u,I0=is} ;
有限時間內破產概率
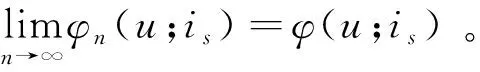
假定保費的收取和索賠均發生在期末,則風險模型的盈余過程為
當n≥1時,
Un=Un-1(1+In)+cδn-Xnεn-Ynξn
(2)
其中U0=u。
2 主要結果
引理1令Mn=Xnεn+Ynξn,{Mn}n≥1是取正值的獨立同分布的隨機變量。設Mn的分布函數為FM(m),則
證明: {Mn}n≥1是取正值的獨立同分布的隨機變量。因此,當m<0時,FM(m)=0。
當m=0時,
FM(0)=P(Mn=0)=P(εn=0)P(ξn=0)=q1q2。
當m>0時,
FM(m) =P(Mn≤m)=P(εn=0)P(ξn=0)+P(εn=1)P(ξn=0)P(Xn≤m)
得證。
由引理1,式(2)的盈余過程即為
(3)
定理1破產概率φ(u;is)滿足以下積分表達式:
證明:由式(3)可知
U1=u(1+I1)+cδ1-M1,
因此,
P(U1<0|I0=is,I1=it,M1=m)
=q3P(u(1+it)-m<0|I0=is,I1=it,M1=m)
+p3P(u(1+it)+c-m<0|I0=is,I1=it,M1=m)
假設
對m進行如下分情況討論:
① 0≤m≤u(1+it)時,
=E(φn(u(1+it)+cδ1-m;it))=q3φn(u(1+it)-m;it)+p3φn(u(1+it)+c-m;it) ;
②u(1+it) =q3+p3φn(u(1+it)+c-m;it) ; 對以上三部分利用全概率公式可得: 證畢。 定義1對于風險過程{Un},若E(M1-cδ1)<0,且存在一個常量R0>0,滿足E(eR0(M1-cδ1))=1,則稱R0為調節系數。 證明:風險過程{Vn}的現實意義為n時刻盈余值貼現到當前時刻的現值,因此可知,風險模型(3)的破產概率等價于風險過程{Vn,n=1,2,…}的破產概率,即 對于式(3)的風險盈余過程{Un},可令 (4) 則 (5) 令Wn=Mn-cδn,即第n階段保險公司凈損失額,分布函數為FW(w)。 式(4)、(5)分別簡化為 (6) (7) 另假定E(W1)<0,存在ρs>0滿足 E(eρsW1(1+I1)-1|I0=is))=1,s=0,1,…,N, 對于?s=0,1,…,N,構造函數 則 因此,ls(r)是一個凸函數,且ρs是方程ls(r)=0在(0,∞)上的唯一正根。 又由詹森不等式可知, 即ls(R0)<0。因此,可得R0≤ρs。 現定義對于所有的s=0,1,…,N, (8) 因此,對于所有的s=0,1,…,N,ls(R1)≤0, E(eR1W1(1+I1)-1|I0=is)≤1 。 (9) 令Sn=e-R1Vn,則 因此,根據詹森不等式及式(9)可得, 即證得常數R1>0使得{e-R1Vn}是一個上鞅。 定理2對所有的s=0,1,…,N, φ(u,is)≤e-R1u,u≥0且e-R1u≤e-R0u。 證明:令Ts=min{n:Vn<0|I0=is},則Ts是一個停時且n∧Ts=min(n,Ts)是一個有限停時,對所得上鞅應用最優停時定理,可得 E(Sn∧Ts)≤E(S0)=e-R1u, 則 e-R1u≥E(Sn∧Ts)≥E(Sn∧TsI(Ts≤n))=E(STsI(Ts≤n)) =E(e-R1VTsI(Ts≤n))≥E(I(Ts≤n))=φn(u,is) 。 當n→∞時,可得 φ(u,is)≤e-R1uu≥0 。 (10) 由式(8)可知R1≥R0,即 e-R1u≤e-R0u, 證畢。 由上述論述可知,R0是定義的沒有考慮風險投資情況的模型(1)的調節系數,即{e-R0Un}是一個鞅,根據停時定理可得模型(1)的Lundberg不等式為φ(u,is)≤e-R0u;將考慮風險投資情況的模型(3)中n時刻盈余值貼現到當前時刻的現值得到模型(4)后,該模型存在R1使得{e-R1Vn}是一個上鞅,同理利用停時定理可得模型(4)的Lundberg不等式為φ(u,is)≤e-R1u;n時刻盈余值的正負情況與其貼現值的正負情況相同,因此考慮風險投資情況的模型(3)的Lundberg不等式也為φ(u,is)≤e-R1u。 又根據函數的凹凸性、極值定理及詹森不等式的相關性質可知,R1≥R0,進一步可得e-R1u≤e-R0u,即考慮投資情況的模型(3)的破產概率上界小于不考慮投資情況的模型(1)的破產概率上界,保險公司進行風險投資可降低風險。 本文主要研究了帶有馬爾科夫鏈利率的離散時間雙險種復合雙二項風險模型,是對已有文獻中相關離散時間風險模型的拓展。 先從險種、保費收取、索賠三個方面進行改進,并通過建立馬爾科夫鏈引入隨機利率,得到更為復雜的風險過程的表達式,并利用遞推法及全概率公式進一步推導出破產概率的積分表達式。隨后研究破產概率上界,通過等價變換得到新的風險過程,在構造函數的基礎上利用詹森不等式證明該風險過程是一個上鞅,通過運用停時定理推導出破產概率上界。研究還發現所討論的帶隨機利率的離散時間雙險種復合雙二項風險模型的破產概率上界優于經典離散時間模型的Lundberg上界,即保險公司進行風險投資將有效降低破產概率。接下來的研究將主要集中于保險公司進行風險投資的實證研究,旨在為保險公司的現實經營提供更具價值的參考。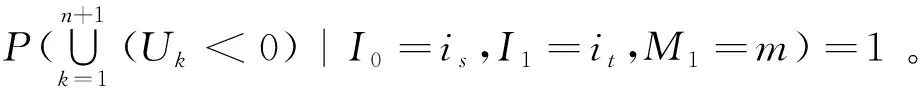
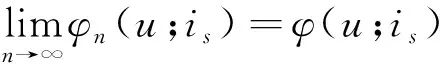
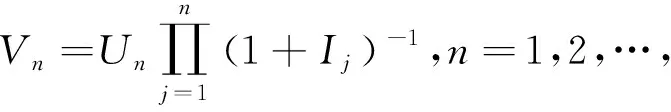

3 結論

