一類帶有脈沖的生物入侵隨機模型的分析
,
(北京科技大學 數理學院,北京 10083)
1 模型介紹
生物入侵是指某種生物從外地自然傳入或人為引種后成為野生狀態,并對本地生態系統造成一定危害的現象。本研究從問題出發,根據生物入侵的特點建立所需的隨機模型并進一步研究模型的性質。
自然界中,物種之間的關系始終受到白噪聲的干擾。因此,很多學者在經典的捕食者食餌模型即Lotka-Volterra模型中加入白噪聲[1-4],得到
其中,x(t)是食餌的種群密度,y(t)是捕食者的種群密度,bi、ci、σi均為非負常數,Bi(t)為標準的布朗運動。
在Lotka-Volterra模型之后,Leslie對其進行改進[5],得到
在食餌增長中,p(x)反映單位時間里每個捕食者吃掉的食餌數量,不僅與食餌的數量有關,還與捕食者的捕食能力有關,稱為捕食者對食餌的功能性反應。這個模型假設捕食者在環境中的最大容量與食餌的數量成正比例,捕食者的增長是關于y(t)的邏輯斯蒂增長方程,其固有增長率為a2,環境最大容納量為a2x(t)/b2。
將Leslie模型中的p(x)取c1x(t),并加入隨機項,有
此模型中,食餌的變化與自身一次項呈正相關,與自身二次項和交叉項呈負相關,此食餌可看作食物鏈較低端的物種;捕食者的變化與自身成邏輯回歸關系,并且其最大環境容納量受食餌數量的限制,此捕食者可看作以一種食餌為食的捕食者。綜上所述,可運用該模型來研究生物入侵。一般情況下,模型中的參數是受時間影響的,例如有些物種的數量變化率就隨季節不同而變化,故模型可變為
進一步考慮現實生活,物種數量會受到來自自然或人類社會的其他影響,比如火山爆發、瘟疫或人類突然的大量捕撈等,這些干擾不是白噪聲的隨機干擾所能涵蓋的。因此,有必要在模型中加入脈沖項[6]
(1.1)
其中,ai(t),bi(t),σi(t)(i=1,2),c1(t)均是正的有界連續T周期函數,并滿足
考慮到是生物模型,故僅需研究方程的正解。因此可做下面限制:
1+δik>0,i=1,2;k=1,2,3,…。
而且,δik>0是物種數量突然增多,代表著對物種的“種植”,δik<0是物種數量突然減少,代表著對物種的“收割”。
此模型的環境干擾有兩種:白噪聲干擾和脈沖干擾。白噪聲干擾使物種連續地變化,而脈沖干擾使物種離散地變化。
此外,這里假定存在正整數p,使得
tk+p=tk+T,δi(k+p)=δik,k∈Z+。
不失一般性,假設
[0,T)∩{tk,k∈Z}={t1,t2,…,tp}。
2 系統正解存在唯一性
定義1[7]考慮一個帶有脈沖的隨機微分方程
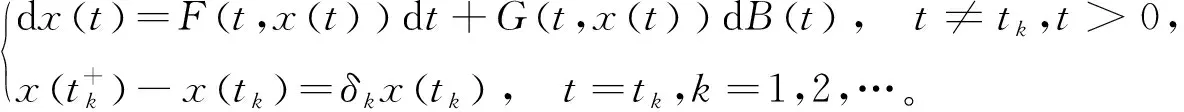
(2.1)
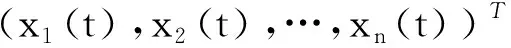
1)x(t)是適應的并且在(0,t1)和(tk,tk+1),k∈N+上都連續,而且F(t,x(t))∈L1(R+;Rn),G(t,x(t))∈L2(R+;Rn)。其中若有f(t)∈Lk(R+;Rn),則
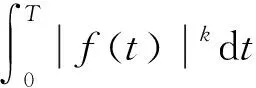
3) 對幾乎每個t∈R+ k,x(t)滿足與(2.1)等價的積分方程,并滿足t=tk,k∈Na.s.時的脈沖條件,則x(t)是系統(2.1)的解。

證明:首先,考慮如下無脈沖項模型
(2.2)
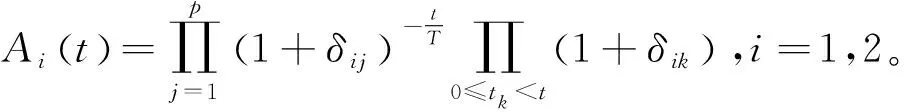
下面證明Ai(t)均是T-周期連續函數。
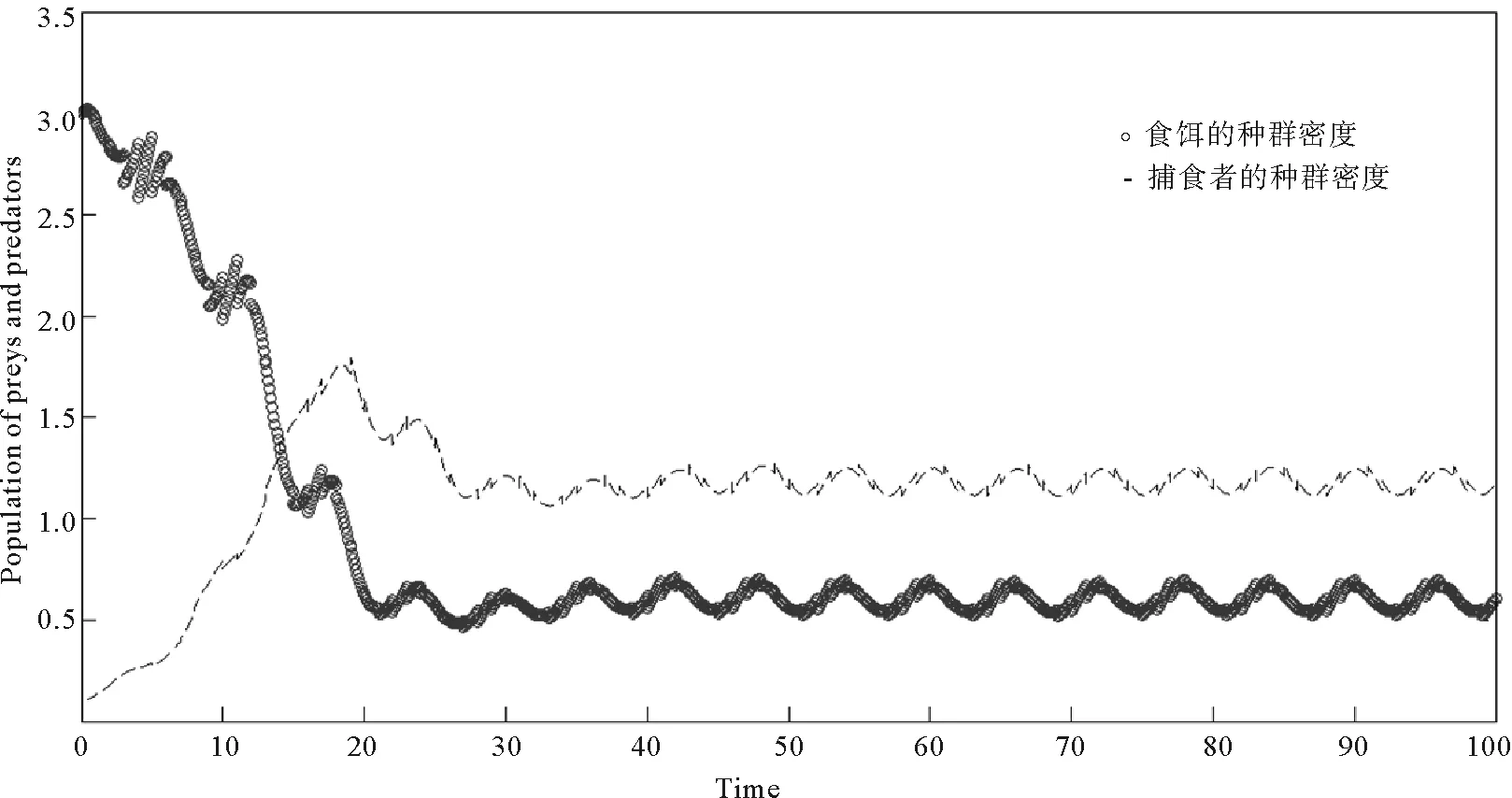
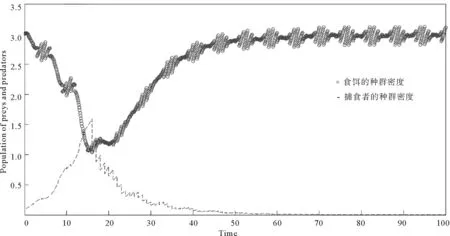
對于任意t,存在整數n,使得nT 由tk+p=tk+T,δi,k+p=δik,得 tk+np=tk+(n-1)p+T=…=tk+nT,δi,k+np=δi,k+(n-1)p=…=δik。 (2.3) 由[0,T)∩{tk}={t1,t2,…,tp},存在l∈{1,2,…,p},使得 (tl+np,tl+1+np,…,tp+np∈[t,(n+1)T), (2.4) 由式(2.3),(2.4)得 故 Ai(t)均是T-周期連續函數,證畢。 然后令x(t)=A1(t)y1(t),y(t)=A2(t)y2(t)。則易知x(t),y(t)在t∈(tk,tk+1)上均連續,k=0,1,2,…,t0=0。 那么當t∈(tk,tk+1)時,有 dx(t) =y1(t)dA1(t)+A1(t)dy1(t) =x(t)(a1(t)-b1(t)x(t)-c1(t)y(t))dt+σ1(t)x(t)dB1(t)。 且有 同理,y(t)在t∈(tk,tk+1)滿足 而且 綜上可知,(x(t),y(t))是滿足系統(1.1)的解,即系統(1.1)存在解(x(t),y(t))。 最后,證明系統(1.1)解的非負唯一性[9]。 取(u(t),v(t)),滿足 x(t)=eu(t),y(t)=ev(t)。 則在t∈[0,t1]上對x(t),y(t)運用It公式得 易知上面方程滿足利普希茨條件,存在唯一的解(u(t),v(t))。而由于x(t)=eu(t),y(t)=ev(t),則(x(t),y(t))為系統(1.1)在t∈[0,t1]上的唯一正解。 同樣在t∈(tk,tk+1](k=1,2…)時,運用It公式得 同樣,上面方程滿足利普希茨條件,存在唯一的解(u(t),v(t))。則(x(t),y(t))為系統(1.1)在t∈(tk,tk+1](k=1,2…)上的唯一正解。 定理證明完畢。 為了后面分析的方便,此處做一些記號。若f(t)是可積的,定義 若f(t)是有界的,定義 定理3.1若滿足 則系統(1.1)中的兩種群最終將滅絕。 證明:對于系統(2.2),運用It公式有 兩邊同時積分并除以t,有 由鞅的強大數定律得 因此有 定理3.2若滿足 則在系統(1.1)中,捕食者最終將滅絕,食餌數量最終將持久。 證明:由定理3.1可知: 捕食者最終將滅絕,下面證明食餌數量的持久性。 等式兩邊同時積分并除以t有 (3.1) 由定理3.1得 那么,方程(3.1)變為 整理可得 可知食餌數量持久,所證成立。 定理3.3若滿足 則在系統(1.1)中,捕食者與食餌數量最終將持久。 證明:在此定理條件下也可得定理3.2中的(3.1)式,對t取極限整理得: 則 由于x(t),y(t)均為非負值,故二者至少有一方種群密度持久。 假設存在t0使得x(t0)=0,由系統(1.1)知當t>t0時必有y(t)=0,兩種群均滅絕,與結論有矛盾,故對所有t>0都有x(t)>0,那么種群密度x(t)將持久。 等式兩邊同時積分并除以t,有 對t取極限整理有 那么 由于對所有t>0都有x(t)>0,且x(t)持久,則x(t)必有下界x0>0,則 為驗證前面的分析,對系統(1.1)進行數值模擬。 此模型可應用于生物入侵的例子。例如澳洲的兔災,1859年,25只歐洲兔子被帶入澳洲供人打獵,但后來兔子沒有天敵,卻有豐富的青草,繁殖過快,給生態帶來了危害。這時人們希望兔子種群能滅絕,青草被保護起來。那么模型中的捕食者就是兔子,食餌是青草,環境干擾是白噪聲干擾,而脈沖干擾就是人類的干預。為了實現研究目的,由定理3.2可知,可通過人為干預,大量捕殺兔子,設法滿足定理3.2中的條件,則最終兔子會滅絕,且青草會持久生存。 在人類干預之前,可看作是脈沖很小的模型,而且是適用一般的隨機模型,主要是隨機因素對模型的影響,不少學者已對此進行過大量研究,在此主要研究脈沖因素對生物入侵的影響。因此可取(x0,y0)=(3,0.1),a1(t)=0.35+0.1sin(πt/3),b1(t)=0.1+0.05sin(πt/3),c1(t)=0.2+0.2sin(πt/3),a2(t)=0.2+0.1sin(πt/3),σ1(t)=σ2(t)=0.01+0.01sin(πt/3),b2(t)=0.1+0.1sin(πt/3)。則有n=p=6。首先看脈沖影響較小的時候,可令: δ1k(t)=-0.05+0.05sin(πk/3),δ2k(t)=0.05sin(πk/3),tk=k。 式中的-0.05反映了環境在一定程度上受到了污染,食餌作為食物鏈的底層物種首當其沖,而對于入侵的捕食者來說則影響較小,故而產生兩種群脈沖項的差異。模擬程序見附件1[12],模擬結果如圖1所示。 圖1 無人類干預時食餌和捕食者的種群密度變化的對比 由參數計算有 由定理3.3知,兩種群密度均為持久的,此結論與圖1的結果相同。 此處食餌為植被或是食物鏈的低端物種,生態系統中原來必然存在一些以其為食的消費者,而此處食餌種群密度保持在正常水平的1/6左右,數量變化過大,長久處于此狀態,生態系統必然遭到嚴重破壞。 研究目標是在食餌數量為正常水平的基礎上,使入侵的捕食者滅絕。因此,可以改變脈沖項,脈沖項可視為人類對入侵物種的干擾,對食餌不構成干擾。考慮到實際情況更多是,只有當外來物種繁殖生長影響生態環境時,人類才會意識到物種的入侵,故有時間上的延遲,將捕食者的脈沖項修改為 δ2k(t)=-0.25×(k>15)+0.05×sin(πk/3)。 其中(k>15)為邏輯語言,當k>15時,(k>15)=1,當k≤15時,(k>15)=0。這個脈沖項的意思是在第16周期時,人類開始對入侵者進行干預,干預強度為每次使其數量減少1/4。 同樣用Matlab得到人類干預時食餌和捕食者的種群密度變化的對比如圖2。 圖2 人類干預時食餌和捕食者的種群密度變化的對比 由參數計算有 則由定理3.2知,此模型捕食者最終將滅絕,食餌數量最終將持久,與圖2的結果相符。 圖2為在第16周期人類對入侵生物進行干預,在16周期前,食餌種群密度最小值接近1,為正常密度的1/3左右。考慮到生態系統的自我恢復能力,食餌種群密度最小值會有一個臨界比例值,而此臨界值會隨著生態系統復雜度的不同而不同。假設一個生態系統的此臨界值為P0。通過調試Matlab可得表1數據值。 表1 人類不同時間干預時食餌種群的最低臨界值 再通過臨界值P0與P的比較得出一個臨界周期k0。因此,人類要在生物入侵后物種成長的第k0周期前及時干預,才能保證生態系統的可逆恢復。
t1+(n+1)p,t2+(n+1)p,…,tl-1+(n+1)p∈[(n+1)T,t+T)。)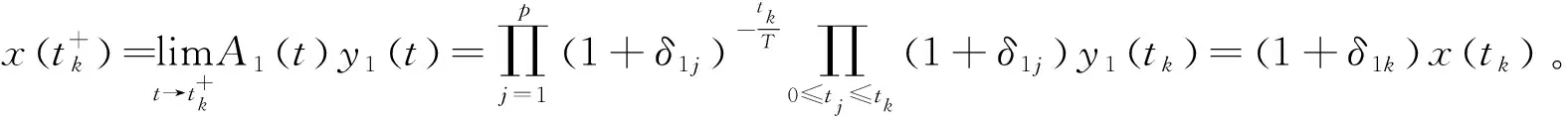
3 滅絕與持久的條件
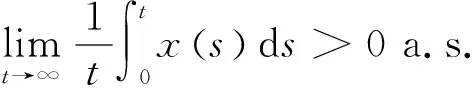
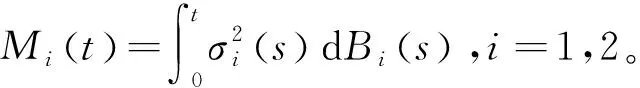
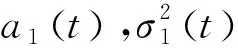
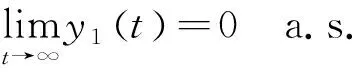
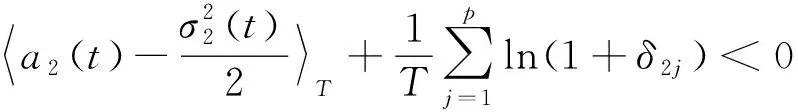
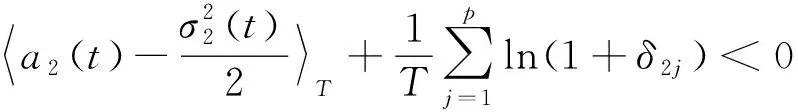

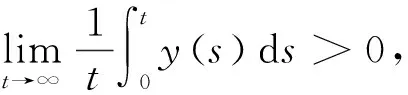
4 數值模擬和結論