一類分數階 SEIS 模型的穩定性分析
,
(山東科技大學 數學與系統科學學院,山東 青島 266590)
傳染病歷來是危害人類身體健康的大敵,從古至今傳染病傳播給人類的生存和國際民生都帶來了巨大的災難[1-2]。定量或定性的研究傳染病傳播的機制可以為預防和控制疾病提供重要的基礎。
文獻[3-5]研究了一類整數階SIS(susceptible-infective-susceptible)傳染病模型,討論了平衡點的穩定性。對于一些具有潛伏期的傳染病,像流感、狂犬病等,應考慮潛伏性,因此有必要研究SEIS(susceptible-exposed-infective-susceptible) 傳染病模型[6-7]。文獻[7]分析了整數階SEIR(susceptible-exposed-infective-recovery)模型的穩定性并提出了SEIS模型。文獻[8]提出了一種考慮治療的新型SEIS模型的活動患者和潛在患者,文獻[9]對此模型的穩定性進行了分析。然而上述文獻均沒有考慮模型為分數階的情形。
分數階微積分是微積分的一個分支,主要研究任意階積分和導數的理論及其應用,最早是于 1695 年由 Leiblilz 和 L’Hospital提出。分數階微積分作為整數階微積分的一種推廣,是伴隨整數階微積分的發展而產生的,已有 300 多年的歷史。目前傳染病模型絕大多數是用常微分方程組、差分方程組、偏微分方程組或時滯微分積分方程組描述的,所涉及到的方程階數均為整數階。整數階導數具有局部性,不適合描述具有歷史依賴的過程模型;分數階導數具有全局相關性,能較好地體現系統函數發展的歷史依賴過程[10-12]。基于以上分析,將分數階引入到傳染病建模具有非常重要的現實意義。
文獻[13]分析了如下分數階SIS模型的平衡點的穩定性,得出該模型的平衡點在α=1,0.9,0.8時都是穩定的。
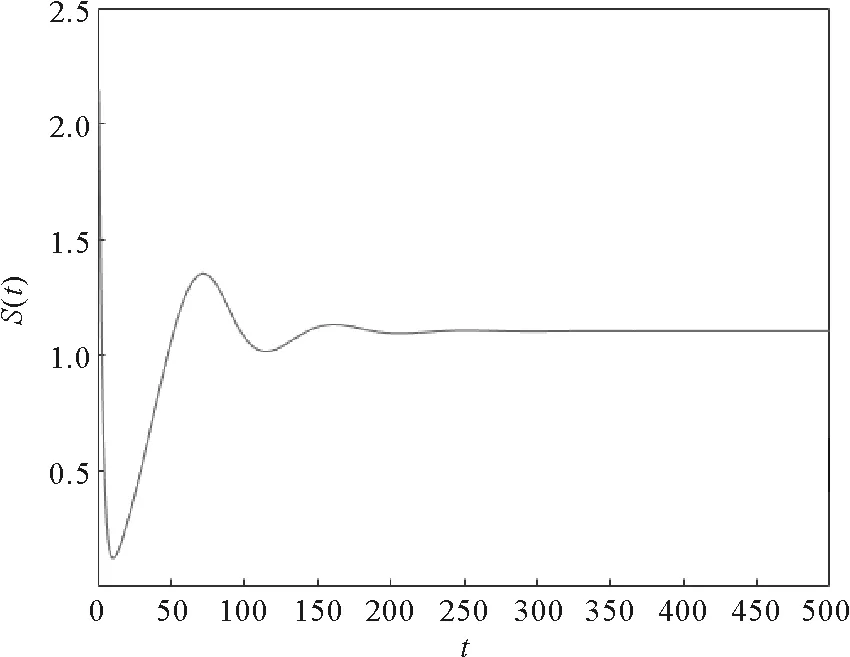
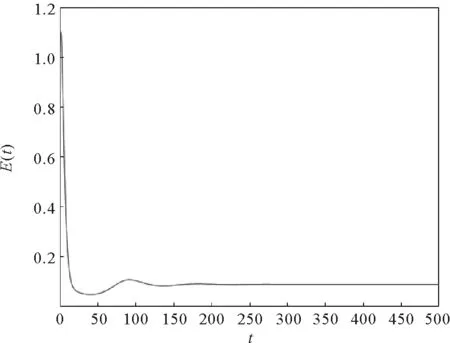
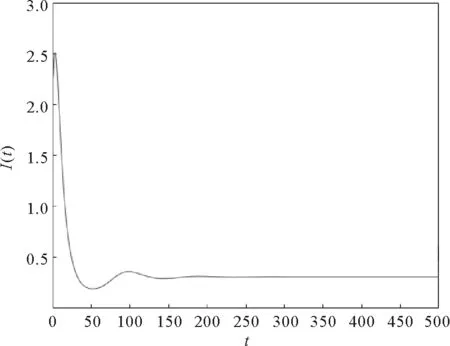
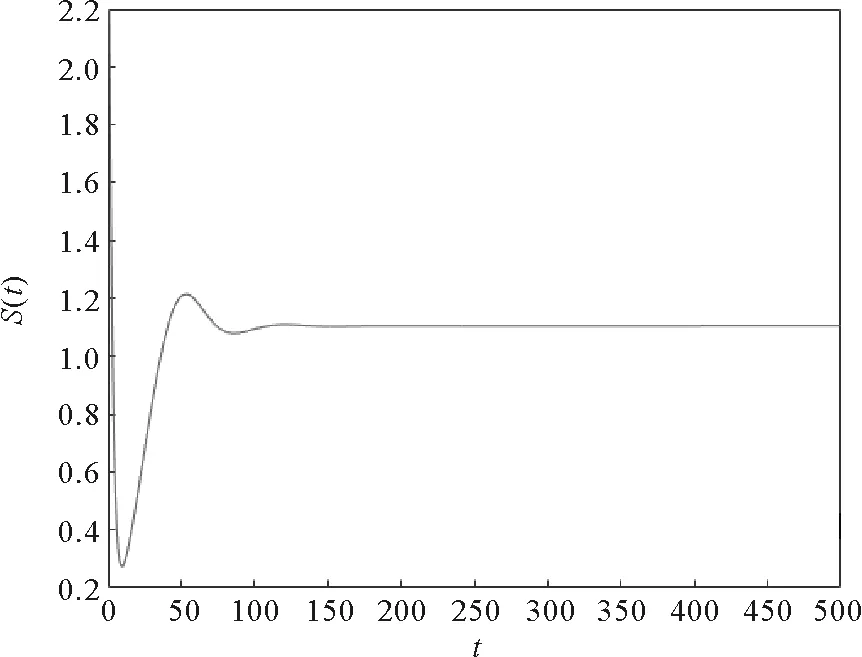
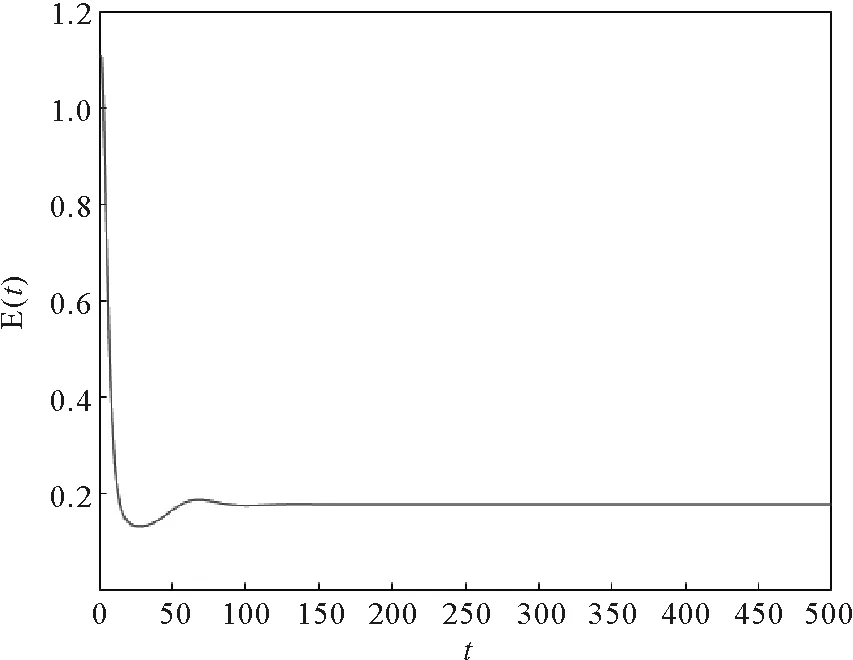
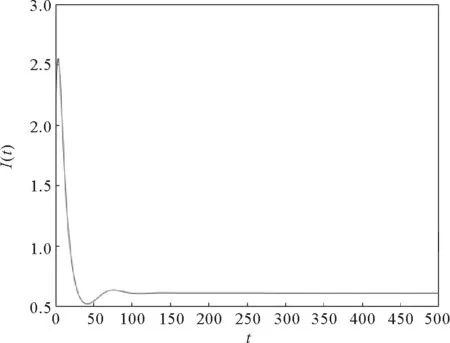
其中:0 文獻[14]提出了如下不考慮治療的分數階SIR模型并對模型的平衡點的穩定性進行了分析,得出模型地方病平衡點和無病平衡點都是局部漸進穩定的,并且具有唯一的一致李雅普諾夫穩態正解。 其中R代表康復者的數量,其余的參數同上。作者進一步考慮了具有治療的分數階SIR流行病模型,提出模型: 并對模型的平衡點穩定性進行了分析,得到了后向分支發生的條件。 結合文獻[9]中的SEIS模型,本文提出如下分數階SEIS模型: (1) 下面將證明該模型平衡點的存在唯一性,分析其無病平衡點和地方病平衡點的局部穩定性和全局穩定性;并通過數值仿真驗證其理論分析的正確性。 定義1[15]函數f(t)的Caputo分數階微積分的定義為: 其中Γ(.)是伽馬函數,n-1 引理1[16]考慮具有Caputo分數階導數的非線性微分方程 DaX(t)=f(X(t))。 (2) 引理2[17]假設f(t)∈C[a,b]且Daf(t)∈C[a,b],a∈(0,1]。若Daf(t)≥0,?t∈[a,b],則對每個t∈[a,b],f(t)是非減函數;若Daf(t)≤0,?t∈[a,b],則對每個t∈[a,b],f(t)是非增函數。 引理3[17]假設向量函數f(t,x):R+×Rn→Rn(維數n≥1)滿足 1)f(t,x)在R+上關于t是Lebesgue可測的; 2)f(t,x)在Rn上關于x是連續的; 的解x(t)在R+上存在且唯一。 定義2[18]設Ω是Rn中的一個開子集,考慮下面的自治系統 Rn=f(x),f(0)=0。 (3) 若V(x)∈C1(Ω,Rn),則V(x)沿著方程(3)解的α階導數為 引理4[18](分數階系統LaSalle不變原理)設D是下列系統的一個正不變集,若?V(x):D→R,具有連續一階偏導數,使 DαV|(3)≤0。 又設E={x|DαV|=0,x∈D},M?E是最大不變集,則當t→+∞時,有x(t,t0,x0)→M,特別地,若M={0},則系統的平凡解是吸引的。 證明: 首先,說明系統存在唯一解。根據引理3,系統的向量函數為 顯然,f滿足引理3的1),2),4)三個條件,為了證明系統(1)解的存在唯一性,只需證明向量函數f滿足引理3中的條件3)。 令x1(t)=S(t),x2(t)=E(t),x3(t)=I(t),x(t)=[x1(t),x2(t),x3(t)]T,μ=[A,0,0]T, 則系統方程可以簡寫為: Dαx(t)=A1x(t)+A2x(t)x3(t)+η 則: 其次,證明系統(1)解的非負性,由系統(1)得 將系統(1)的3個方程相加并變形得: DαN=A-μ(S+E+I)=A-μN, 其中N=S+E+I, 定理2如果0 證明:當無病毒感染(I=0)時,系統(1)始終存在一個無病平衡點 且在無病平衡點E0處的雅可比矩陣為: 特征方程為: 整理得 系統(1)的無病平衡點E0的穩定性取決于特征方程的根位置。 當方程的所有根位于復平面的左半平面,則無病平衡點E0穩定。 易知一個特征根λ1=-μ,那么只需要討論下面的等式 計算可得 (4) 根據韋達定理可得 (5) 可得 (β+r1+μ)(μr2+μ2-αpA)-β(1-p)αA>0。 推出 (6) 容易得到 Reλ2<0,Reλ3<0, 又有 λ1=-μ。 因此,當0 定理3如果R0>1,地方病平衡點E1(S*,E*,I*)是局部穩定的。 證明:設E1(S*,E*,I*)為地方病平衡點,則有 (7) 解得 系統(1)在E1(S*,E*,I*)處的雅可比矩陣為: 其特征方程為: 注意到,當λ=-μ時特征方程等于0,即: (8) 容易得到存在一個特征根 λ=-μ。 (9) 令λi(i=1,2,3)是矩陣J(E1)的特征值;可以假設λ1=-μ特征方程可以重寫為: (λ+μ)[λ2+(2μ+r1+r2+β-pαS*+αI*)λ+(r2+μ)(1-p)αI* +(r2+μ)pαI*+(r1+μ)pαI*+βαI*]=0。 (10) 只需考慮: λ2+(2μ+r1+r2+β-pαS*+αI*)λ+(r2+μ)(1-p)αI* +(r2+μ)pαI*+(r1+μ)pαI*+βαI*=0 。 (11) 由韋達定理可得 λ2+λ3=(pαS*-r2-μ)-μ-β-αI*-r1 λ2λ3=(r2+μ)(1-p)αI*+(r1+μ)pαI*+βαI*>0。 容易得到 Reλ2<0,Reλ3<0, (12) 又有λ1=-μ<0。因此Reλi<0(i=1,2,3),所以E1是局部穩定的。證畢。 定理4如果0 證明:令 V(t)=βE(t)+(β+r1+μ)I(t) (13) 則V沿著系統(1)的解的α階導數為 DαV|(1)=I1-αDV|(1) =(β(1-p)αS(t)+(β+r1+μ)pαS(t) -(β+r1+μ)(r2+μ)I(t) (14) 若R0<1,可以得到 (15) 由V(t)=βE(t)+(β+r1+μ)I(t)和β+r1+μ>0可得 (16) 其中V(0)=βE(0)+(β+r1+μ)I(0)。 由R0<1可得 因此可得 當R0>1時,存在正數ε,使得 β(1-p)α≥(β+r1+μ)(r2μ+μ2+pαA)+ε。 (17) 根據DαV|(1)=(β(1-p)αS(t)+(β+r1+μ)pαS(t)-(β+r1+μ)(r2+μ)I(t)得: (18) 從該地區開始的系統(1)的解 (19) 遠離E0。證畢。 模型參數取為:a=0.99,A=0.3,α=0.7,β=1,p=0.4,μ=0.5,r1=0.1,r2=0.1,S(0)=3,E(0)=1,I(0)=2。 經計算可得R0≈0.364 6<1。根據定理4可得無病平衡點是全局漸近穩定的。仿真結果見圖1~3。 基于上述假設參數值集,選擇A=0.6,可得R0=1.19>1。仿真結果見圖4~6,由仿真可見系統(1)的地方病平衡點是局部穩定的。 圖1 R0<1的系統(1)的S(t)的時間序列Fig.1 Time series of S(t) of the system (1) for R0<1 圖2 R0<1的系統(1)的E(t)的時間序列Fig.2 Time series of E(t) of the system (1) for R0<1 圖3 R0<1的系統(1)的I(t)的時間序列Fig.3 Time series of I(t) of the system (1) for R0<1 圖4 R0>1的系統(1)的S(t)的時間序列Fig.4 Time series of S(t) of the system (1) for R0>1 圖5 R0>1的系統(1)的E(t)的時間序列Fig.5 Time series of E(t) of the system (1) for R0>1 圖6 R0>1的系統(1)的I(t)的時間序列Fig.6 Time series of I(t) of the system (1) for R0>1 主要研究了一類分數階SEIS傳染病模型的無病平衡點和地方病平衡點的穩定性。利用特征根方法得出:當0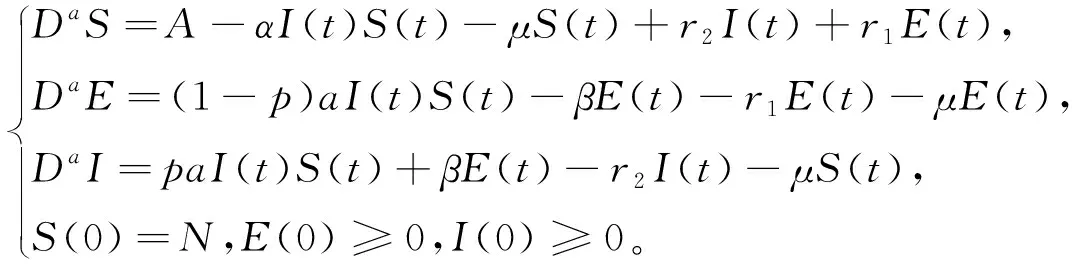
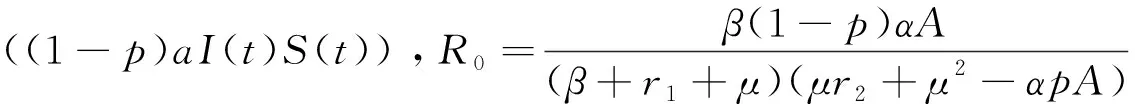
1 基礎知識
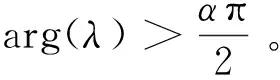
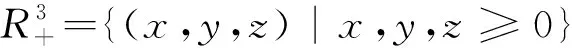

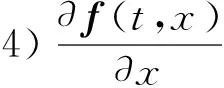
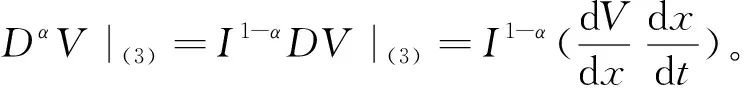
2 平衡點及其穩定性
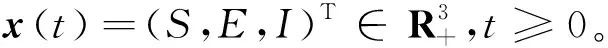
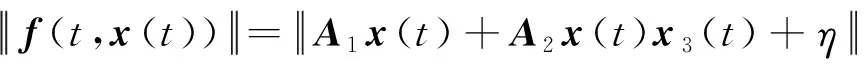
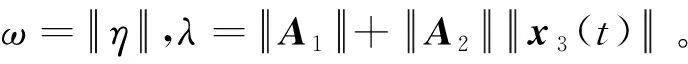
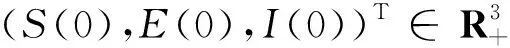
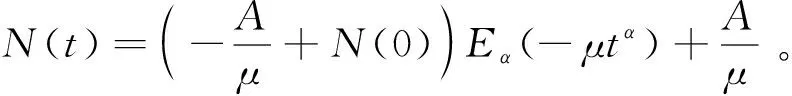
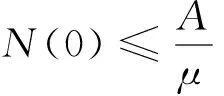

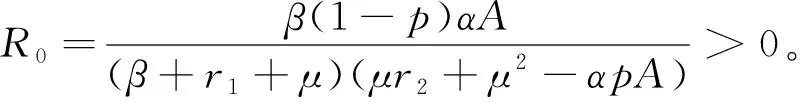
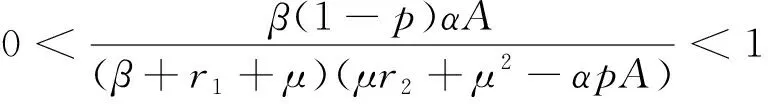
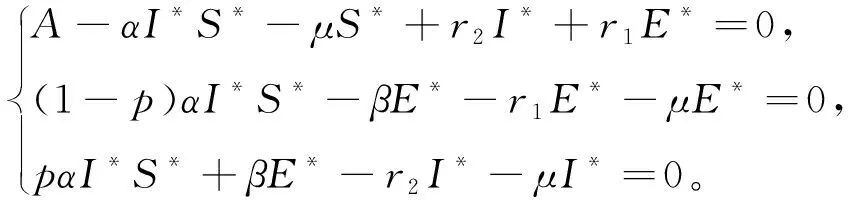

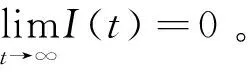
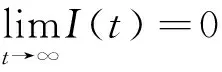
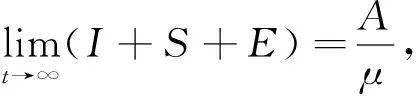
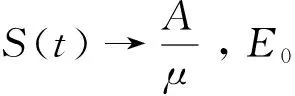
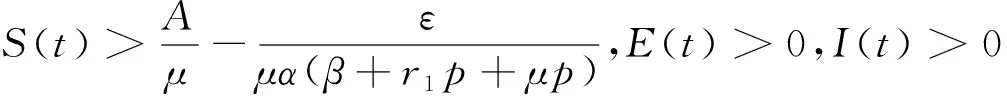
3 數值仿真
4 結論

