基于Laplace先驗的復貝葉斯壓縮感知ISAR高分辨成像算法

朱曉秀,胡文華,馬俊濤,郭寶鋒

(陸軍工程大學石家莊校區電子與光學工程系,河北 石家莊 050003)

0 引 言

逆合成孔徑雷達(inverse synthetic aperture radar,ISAR)具有全天時、全天候、作用距離遠和分辨率高等特點,能夠獲得目標的二維圖像,有利于目標分類與識別,在民用和軍用領域應用廣泛[1]。由雷達成像原理可知,通常采用增加發射信號帶寬和增大觀測角度范圍的方式分別提高距離向和方位向分辨率。在實現ISAR二維成像時,傳統的成像算法如距離多普勒(range doppler,RD)算法有一定局限性。一方面,由于ISAR目標的非合作性,為獲得方位向高分辨,在觀測時間內目標的散射特性可能變化較大[2],利用傳統的初相校正方法后不可避免地存在殘余相位誤差導致圖像散焦[3]。另一方面,RD算法實質上是對回波數據進行快速傅里葉變換(fast Fourier transformation,FFT)處理,會產生較高的副瓣影響成像質量,并且對噪聲抑制能力不強,在低信噪比(signal-to-noise ratio,SNR)條件下得到的ISAR圖像存在較強的干擾噪聲。

壓縮感知(compressed sensing,CS)理論表明,稀疏信號可由求解l1范數最優化問題得到高概率重構[4]。由于ISAR成像的強散射中心僅占整個成像平面非常少的像素單元,說明具有很強的空域稀疏性[2],這吸引了國內外眾多學者研究基于CS理論的ISAR成像方法,并發現利用ISAR圖像的稀疏特性可以在提高成像分辨率的同時能有效地降低副瓣和抑制噪聲。為解決圖像散焦問題,文獻[5]在CS理論的基礎上提出了一種基于貝葉斯估計的ISAR自聚焦成像方法,將運動誤差相位估計和ISAR圖像重構轉化為l1范數約束問題,通過回波數據矢量化并采用數值迭代方法求解最優化問題實現高精度ISAR成像。文獻[6-7]將該方法應用到了稀疏孔徑中,實現了稀疏孔徑自聚焦高分辨成像。但基于l1范數約束的自聚焦成像方法求解時涉及二維數據矢量化、稀疏字典對角化操作,增加了數據存儲量和運算復雜度,且該類算法只利用了目標圖像的稀疏特性,有時候不能獲得最優稀疏解。文獻[8]進一步考慮了目標圖像的結構信息,利用圖像的聯合稀疏先驗特征,將ISAR自聚焦成像轉化為多測量矢量聯合稀疏優化問題,假設目標圖像各像元服從復高斯分布,提出了一種基于貝葉斯壓縮感知(Bayesian compressed sensing,BCS)的ISAR自聚焦成像方法,進一步改善了自聚焦精度和成像質量。文獻[9]表明,在實數域應用聯合Laplace分布比Gaussian分布具有更好的稀疏促進作用。但由于ISAR回波信號為復數,采用傳統的貝葉斯推理需要將復數轉換為實數后進行求解,增加了運算復雜度。

綜上所述,現有的算法應用到ISAR成像中存在稀疏效果不強、數據存儲量大、運算復雜度高等問題,基于此,本文提出了基于Laplace先驗的復(complex BCS,CBCS)ISAR高分辨成像算法。假設目標圖像各像元服從復Laplace先驗建立稀疏先驗模型,直接對復數信號進行貝葉斯推理,并采用分布式計算方法,先逐距離單元求解其對應的目標像,再逐脈沖求解相位誤差,在提高成像質量的同時減小了數據存儲量和運算復雜度。仿真實驗表明,與基于l1范數約束和基于稀疏貝葉斯學習(sparse Bayesian learning,SBL)的自聚焦成像算法相比,本文的算法具有更好的成像效果。

1 信號模型

利用傳統的成像算法(如RD算法)實現運動目標ISAR二維成像主要是將回波數據先通過脈沖壓縮實現距離向高分辨,再通過目標轉動產生的多普勒信息實現方位向高分辨。在進行方位向處理前,需要將目標運動時產生的與成像無關的平動分量進行補償。假設ISAR回波信號經距離維脈沖壓縮之后,已經做過傳統的平動補償處理。由文獻[10]可知,包絡對齊的精度可以實現小于1/2的距離單元,但相位校正的誤差相位補償精度要求在波長量級,較難達到,因此相位校正后的殘余相位誤差通常不能忽略,會導致圖像散焦,而且在低SNR條件下存在較強的干擾噪聲和副瓣,嚴重影響了成像質量。

ISAR成像時,目標強散射中心雖僅占整個成像平面少量的像素單元,但卻貢獻了目標散射場的絕大部分能量,說明ISAR成像具有很強的空域稀疏性[2],即可將CS理論應用到ISAR成像中。考慮到噪聲和相位誤差的存在,基于CS理論的單基地ISAR成像模型的回波數據用矩陣形式表示為[5]

S=EFA+ε

(1)

國內外已有不少學者基于CS理論的稀疏重構方法進行了研究,并發現利用ISAR圖像的稀疏特性可以有效提高成像分辨率、降低副瓣和抑制噪聲[5]。但一般的稀疏重構方法僅從優化的角度進行了高分辨重構,而沒有考慮與ISAR圖像相關的所有信息,有時無法得到最優稀疏解,重構精度有進一步提高的空間。

2 基于Laplace先驗的CBCS ISAR高分辨成像

BCS理論是在CS理論的基礎上,充分挖掘和利用目標的先驗信息構造信號重構模型,利用貝葉斯統計進行推理,可實現更好的信號恢復效果。由于貝葉斯靈活性高,適用范圍廣,相比于傳統的CS重構算法有一定的優越性,因此本文考慮將BCS理論與ISAR成像相結合,利用ISAR圖像的稀疏性和先驗信息進行BCS框架建模,并利用相應的重構算法實現圖像重構。

目前,在BCS理論重構算法中應用比較廣泛的是基于Gaussian先驗的SBL算法,即假設目標各像元服從Gaussian先驗,通過超參數約束將稀疏先驗模型轉化為二層概率模型,即可轉化為目標像元服從聯合Student-t分布,最后能得到具有稀疏系數的解。有研究表明,在實數域應用由Gaussian先驗和指數先驗共同約束的聯合Laplace先驗比Gaussian先驗具有更好的稀疏促進作用[9]。但其求解方法都是假設處理數據為實數而進行推導的。由于在ISAR成像過程中,雷達接收的回波信號為復數信號,不能直接應用實數域方法進行求解[11],簡單解決辦法是將復數信號轉化為實部和虛部兩個部分,然后再分別利用實數域的推理方法進行求解[12],此時,復數模型可變為

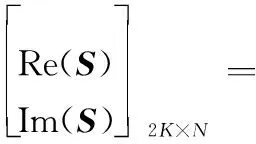
(2)

式中,Re(·)和Im(·)分別表示實部和虛部。可以看出,復數模型轉實數模型后,數據存儲量變為原來的兩倍,運算量也隨之增加。而且,由于實部和虛部的重構過程相互獨立,存在的估計誤差必然會影響其復數相位,進而影響后續的相位自聚焦過程。為避免對復數信號的實部和虛部分別重構,本文假設目標圖像各像元服從Laplace先驗進行稀疏目標建模,提出了一種直接在復數域處理的基于CBCS的ISAR高分辨成像方法。

2.1 目標圖像參數CBCS模型

2.1.1 目標稀疏模型

(3)

對超參數αi可采用指數分布[9]約束,即

(4)

由此,得到新的聯合先驗為

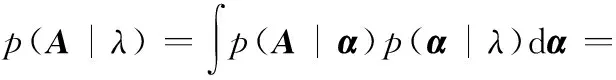
(5)

式(5)表示像元服從Laplace先驗,引入超參數ξ對其中的超參數λ施加Gamma先驗分布,即

p(λ|ξ)=Γ(λ|ξ/2,ξ/2)

(6)

采用此分布為了在一定的限制范圍內,參數λ的先驗分布具有一定的靈活性。

2.1.2 噪聲模型

假設ε是復高斯白噪聲,其中不同元素為獨立同分布隨機變量,服從零均值復高斯分布,即其虛部和實部分別獨立服從方差為σ2的實高斯分布,則回波信號的條件概率密度函數為

(7)

式中,‖·‖F表示矩陣的Frobenius范數。為獲得高斯分布函數的共軛特性,對σ-2施加Gamma先驗分布,即

p(σ-2)=Gamma(σ-2|c,d)

(8)

式(5)和式(6)表明,該稀疏先驗等價于三級貝葉斯模型,分層模型如圖1所示,前兩級表示由指數分布和Gaussian分布聯合約束的Laplace分布,后一級是對參數λ的約束。所以對像元ai的稀疏先驗實際上是通過3層貝葉斯模型ξ→λ→αi→ai依次傳遞實現的。

圖1 CBCS Laplace分層先驗模型Fig.1 CBCS Laplace hierarchical prior model

2.2 ISAR高分辨成像求解過程

考慮到回波中不可避免存在平動補償初相校正后的殘余相位誤差,將會影響重構算法的性能,進而影響成像質量。因此,有必要結合目標圖像稀疏重構和相位誤差校正,研究ISAR高分辨成像算法,提高成像質量。由文獻[5]可知算法要實現相位自聚焦,就需要利用到完整的回波數據,即每次迭代時必須得到整個二維圖像的估計值。傳統的算法在實現目標圖像重構時采用先將矩陣回波數據矢量化,即將二維回波數據逐距離單元拉直為一維矢量,在每次迭代中利用重構算法實現矢量重構,然后再將重構出的矢量結果轉化為二維矩陣形式,即為每次迭代得到的二維目標圖像。若采用這種矩陣矢量化處理的思想,式(1)可表示為

(9)

式中,sn、an和εn分別表示第n個距離單元對應的回波矢量、目標圖像矢量和噪聲矢量。可以看出,回波數據的矢量化、相位誤差矩陣和稀疏字典的對角化不僅構造復雜,而且大大增加了存儲空間,還會影響后續圖像重構時的運算效率。

因此,為避免矩陣矢量化操作,本文在算法求解時提出了分布式計算方法,通過構建新框架,在每次迭代過程中,先逐距離單元利用重構算法處理,將重構結果合成得到二維目標圖像后,再逐脈沖處理實現相位誤差求解,在一次迭代中就可以實現圖像重構和相位自聚焦。這樣不用構造復雜的矩陣,減少了數據存儲空間,而且在目標圖像重構和相位誤差求解時相當于每次只處理一個距離單元或一個脈沖的數據,降低了每次的運算量,有效提高了運算效率。本小節將從目標圖像重構和相位誤差校正兩個方面對分布式計算框架的求解方法進行介紹。

2.2.1 目標圖像重構

對某特定距離單元數據S·n,其CS模型可表示為

EHS·n=FA·n+ε·n

(10)

式中,EHS·n表示消除相位誤差后的數據。

利用式(7)中的條件分布及式(3)、式(4)和式(6)中的稀疏先驗信息,根據貝葉斯規則,若給定αn,λ,σ2,其后驗分布可分解為

p(A·n,αn,λ,σ2|EHS·n)=

p(A·n|EHS·n,αn,λ,σ2)p(αn,λ,σ2|EHS·n)

(11)

式中,p(A·n|EHS·n,αn,λ,σ2)∝p(A·n,αn,λ,σ2,EHS·n),所以p(A·n|EHS·n,αn,λ,σ2)服從均值為μn,協方差為Σn-λ的復高斯分布[9],即p(A·n|EHS·n,αn,λ,σ2)～CN(A·n|μn,Σn-λ),其中

μn=σ-2Σn-λFHEHS·n

(12)

Σn-λ=(σ-2FHF+Λn-λ)-1

(13)

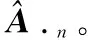
利用式(11)中的p(αn,λ,σ2|EHS·n)估計超參數αn,λ,σ2。由于p(αn,λ,σ2|EHS·n)=p(α,λ,σ2,EHS·n)/p(EHS·n),故p(αn,λ,σ2|EHS·n)∝p(α,λ,σ2,EHS·n),有

p(α,λ,σ2,EHS·n)=

p(α|λ)p(λ)p(σ2)

(14)

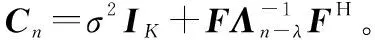
通過最大化聯合分布p(α,λ,σ2,EHS·n),可得到αn、λ、σ2的估計,為方便計算,在對數域進行最大化求解,忽略常數項后建立目標代價函數，即

L=lnp(α,λ,σ2,EHS·n)=

(15)

利用行列式恒等式和矩陣求逆公式,并展開最后一項,可得到代價函數為

(16)

(17)

由于超參數為正值,求解式(17)后舍去負值根,得到αin的更新公式為

(18)

利用式(16)對σ-2求偏導等于零,可得

(19)

求解式(19)得到σ2的更新公式為

(20)

再利用式(16)對λ求偏導等于零,可得

(21)

求解式(21)得到λ的更新公式為

(22)

為計算簡便,令ξ→0,將式(22)代入式(18)可得

(23)

由文獻[14]可知,對目標像施加Gausian先驗時,αin的更新公式為

(24)

兒童FC主要基于典型的病史和體格檢查做出臨床診斷，一般不需要其他理化檢查。其診斷標準，建議采用羅馬Ⅳ標準（以4歲為界分為嬰兒/幼兒 FC 和兒童/青少年 FC）［1］、《巴黎兒童便秘術語共識》（PACCT，沒有年齡限制）［8］等。

2.2.2 相位誤差校正

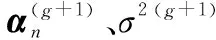
(25)

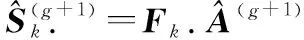
(26)

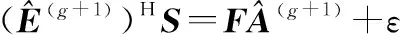
3 ISAR高分辨成像算法實現流程

利用基于Laplace先驗的CBCS ISAR高分辨成像算法實現ISAR成像的流程圖如圖2所示,具體求解步驟如下:

步驟1ISAR原始回波經脈沖壓縮,并做包絡對齊和初相校正后得到可能包含殘余相位誤差的二維回波數據S;

步驟2構造稀疏基字典F,初始化超參數αin=1,σ2=0.01,初始化E=IK,g=1,設定總迭代次數G和門限eps;

步驟3利用相位誤差矩陣E進行回波數據相位誤差補償,得到補償后的回波數據Scom=EHS,即進入圖像迭代過程;

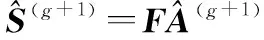
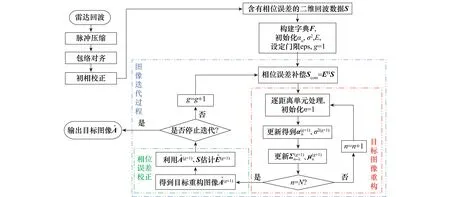
圖2 基于Laplace先驗的CBCS ISAR自聚焦成像算法流程圖Fig.2 Flow diagram of autofocusing algorithm for ISAR imaging based on complex BCS using Laplace priors

4 算法運算量分析

為了更好地比較算法的計算量,本節將進行所提算法的分布式計算方法和矩陣矢量化操作計算方法的運算量分析。以一次加法或乘法為計算量單位,分析每次迭代過程中兩種不同求解方式的計算量。

若采用矩陣矢量化操作進行求解,式(9)表示的矢量化后成像模型可重寫為

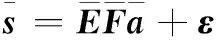
(27)

若利用分布式計算框架逐距離單元進行目標圖像重構,對某一個距離單元處理時,F是K×M矩陣,Λn-λ和Σn-λ是M×M矩陣,E是K×K矩陣,S·n是K×1矩陣,則σ-2FHF的計算量為O(KM2),Σn-λFHEHS·n的計算量為O(KM2+MK2+MK),所以根據式(12)和式(13),更新Σn-λ的計算量為O(M3+KM2),更新μn的計算量為O(KM2+MK2+MK),則本文算法一次迭代中處理N個距離單元實現目標圖像重構的總計算量為O(NM3+2NKM2+NMK2+NMK),與矩陣矢量化操作求解時的O(N2(NM3+2NKM2+NMK2+MK))相比要小很多,可以有效減少運算量,提高運算效率。

5 仿真實驗與分析

通過仿真實驗從運算時間、相位誤差形式和回波SNR 3個方面對本文算法性能進行驗證。運行時間可以反映算法的運算復雜度,體現算法的運算效率;不同形式的相位誤差和不同的SNR會影響迭代的收斂性,進而影響圖像的聚焦效果,特別是低SNR條件下對算法性能要求比較高,否則無法得到良好的聚焦圖像,所以驗證本文算法的運算時間以及在不同相位誤差形式和不同SNR條件下的自聚焦性能是必要的。

本文仿真實驗環境為Windows 7 64位操作系統,Matlab 2016A軟件平臺,仿真所用計算機主要參數如下:處理器為Intel酷睿i5-6200U,主頻為2.30 GHz,內存為4 GB。

5.1 算法運算時間驗證

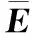
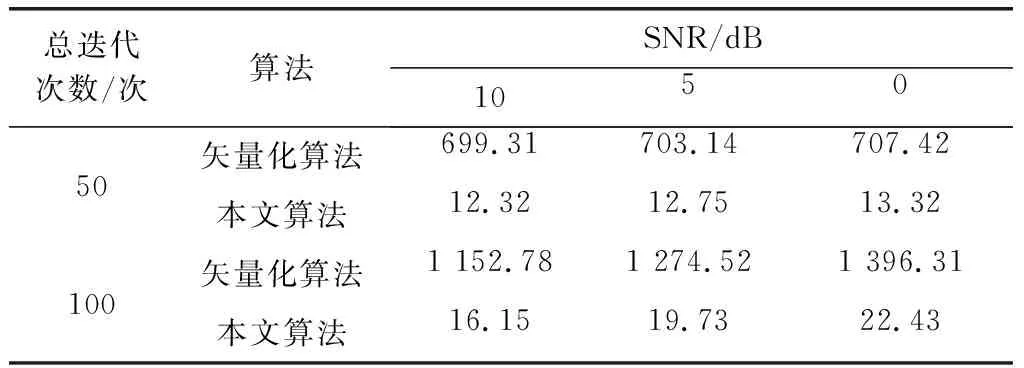
表1 算法運行時間比較Table 1 Comparison of algorithm run time

從表1中數據可以看出,當預設總迭代次數為50次時,相同SNR條件下本文算法的運行時間明顯比矢量化求解算法短,說明了本文算法在提高運算效率方面有明顯的優勢,但由于預設的迭代次數較少,算法無法提前達到收斂條件,兩種算法均迭代了50次,故在不同的SNR條件下同一種算法的運算時間較為相近;當預設總迭代次數為100次時,算法能提前達到收斂條件停止迭代,對于同一種算法,隨著SNR的增大,運算時間有所減少,說明SNR會影響算法的迭代次數,進而影響其運算時間。

5.2 不同相位誤差形式下算法自聚焦性能驗證

通過構建簡單的理想散射點目標模型驗證算法的自聚焦性能。模型如圖3所示,目標一共由14個散射點組成,每個散射點幅度均為1。

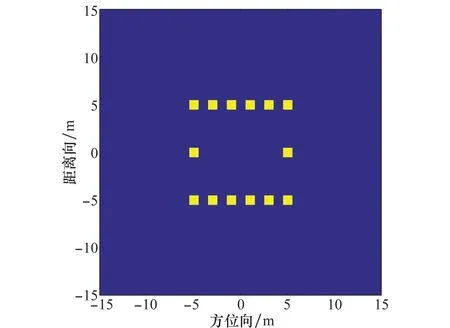
圖3 理想散射點目標模型Fig.3 Target mode of ideal scattering points

為減小運算復雜度,假設回波數據一共有32個脈沖序列且每個脈沖包含32個距離采樣單元,迭代次數為100次。為回波數據添加3種不同形式的相位誤差,以驗證不同形式運動條件下算法性能。第1種為二次相位誤差,主要用于分析由高速運動引起的相位誤差時算法的性能;第2種為正余弦相位誤差,主要用于分析由復雜運動引起的相位誤差時算法的性能;第3種為隨機相位誤差,主要用于分析在由其他不定因素引起的相位誤差時算法的性能。圖4的每行分別表示二次相位誤差、正余弦誤差和隨機誤差條件下的成像結果,其中第1列表示3種不同形式的相位誤差,第2列表示添加相位誤差后的RD算法直接FFT成像結果,第3列表示本文算法的成像結果。

圖4 不同相位誤差形式下的自聚焦性能驗證Fig.4 Verification of autofocusing performance in different phase error forms

可以看出,在3種不同相位誤差形式下,本文算法都有良好的聚焦性能,說明該算法的適用性較強,應用時不用考慮相位誤差的具體形式。

5.3 不同SNR條件下算法自聚焦性能驗證

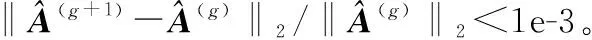
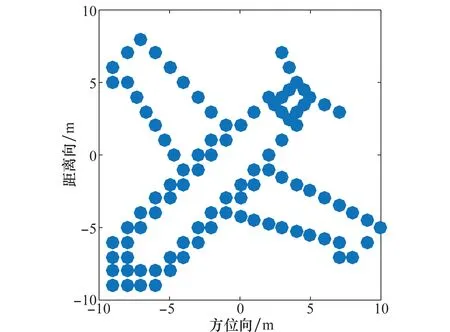
圖5 目標飛機仿真模型Fig.5 Simulation model of target aircraft

為方便直觀比較算法性能,采用目標背景比(target-to-background ratio,TBR)[14-15]、相位誤差提取精度ρ和圖像熵En作為衡量標準,其定義可表示為

(28)

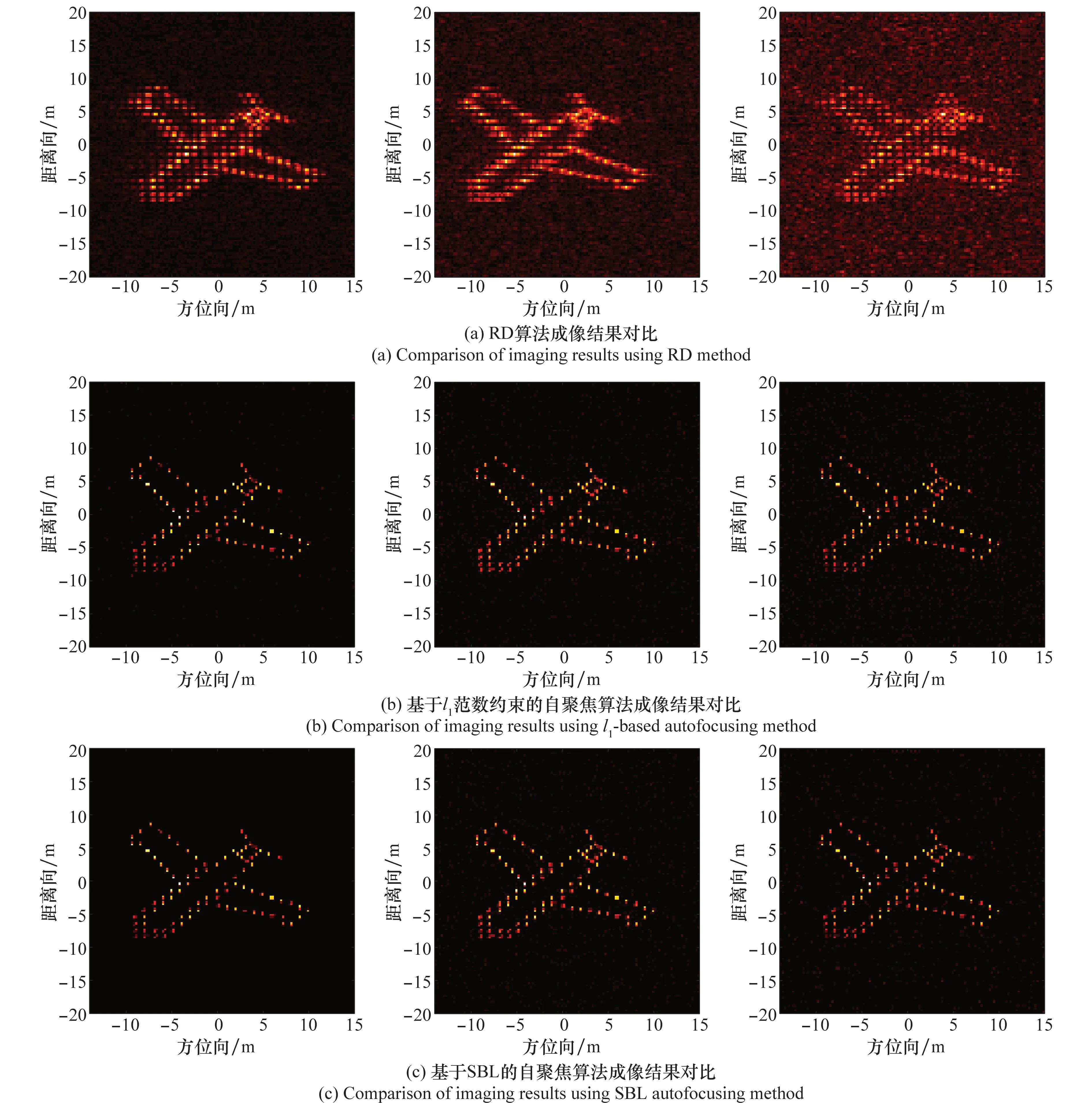
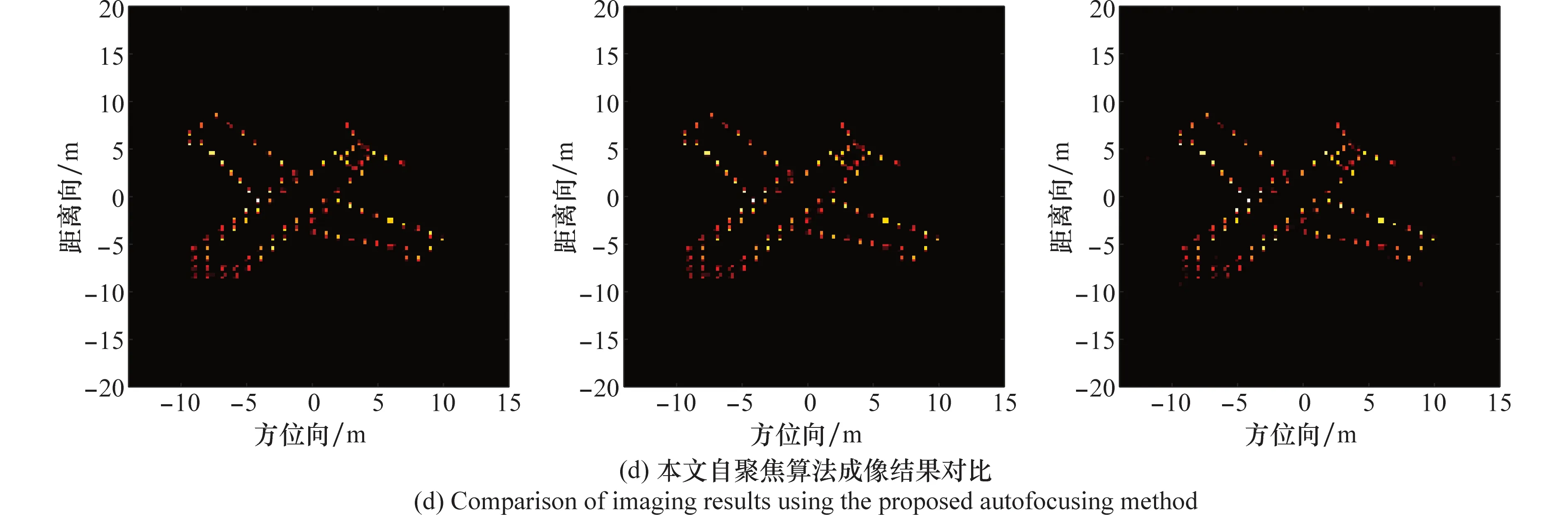
圖6 不同算法在3種SNR下成像結果對比Fig.6 Comparison of imaging results using different methods under 3 different SNRs

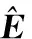
表2 不同算法在3種SNR下評價指標對比Table 2 Comparison of evaluating indicators using different methods under three different SNRs

可以看出,在SNR較高時,3種算法均能較好地實現自聚焦,但隨著SNR降低,基于l1范數約束的自聚焦算法對噪聲抑制效果不佳,比基于BCS框架下的兩種算法成像質量差,有較多的虛假點存在;對比基于SBL的自聚焦算法和本文算法成像結果數據可以看出,隨著SNR降低,本文算法的TBR大于SBL算法,圖像熵小于SBL算法,同時相位誤差提取精度也優于SBL算法,說明本文算法魯棒性更好,能夠在提高圖像自聚焦性能的同時有效實現噪聲抑制。由于SBL算法是基于Gaussian先驗實現的,這也說明了Laplace先驗比Gaussian先驗有更強的稀疏促進作用。

6 結 論

本文利用ISAR圖像的稀疏先驗信息、整體結構信息以及噪聲模型統計信息,提出了基于Laplace先驗的CBCS ISAR高分辨成像算法,在目標圖像重構的同時實現相位誤差更新。相比于Gaussian先驗和傳統的稀疏先驗模型(如l1范數約束),該算法有更強的稀疏促進作用。在求解過程中,直接對復數信號進行貝葉斯推理,采用分布式計算方法將距離維和方位維分開處理進行求解,減小了數據存儲量、降低了運算復雜度,并進一步提高了成像質量。仿真實驗表明,在不同相位誤差形式和低SNR條件下,該算法都有良好的自聚焦性能。