基于模糊約束的軍事物資配送多目標路徑優化
趙文飛,孫璽菁,司守奎,劉孝磊
(海軍航空大學航空基礎學院,山東 煙臺 264001)
0 引 言
近年來,隨著信息化程度的提高、武器裝備的不斷發展,現代高技術局部戰爭呈現海、陸、空、天、電等多維態勢,戰爭具有突發性強、節奏快、作戰半徑大、作戰物資消耗大等特點。因此,現代戰爭要求軍事物流系統必須做到快速反應、保障充分,并且隨著戰場形勢的變化需要適時地調整軍事物資的保障方案。而軍事物資運輸調度作為實現戰時后勤保障精確化的關鍵環節,已成為現代信息化戰爭取勝的必要條件,所以構建合理的軍事物資配送網絡模型及運輸路徑的優化問題一直以來是各國軍事物流研究的熱點[1-4]。
軍事物資運輸問題往往是非線性多目標規劃問題,屬于non-deterministic polynomial (NP)問題,目前用于求解該問題的主要方法有遺傳算法、蟻群算法、模擬退火等智能算法。例如文獻[5]等針對現代軍事物流中的車輛路徑問題(fuzzy vehicle routing problem,VRP),建立了戰時軍事物流多目標VRP數學模型,該模型采用非支配排序遺傳(non-dminated srting gnetic agorithm-Ⅱ,NSGA-Ⅱ)算法求解;文獻[6]研究了車輛裝備保障運輸網絡,提出了基于蒙特卡羅仿真和遺傳算法的車輛裝備運輸網絡化模型;文獻[7]針對物流配送車輛優化調度問題,建立了多目標的優化模型,并設計了基于多目標的蟻群算法進行求解。而戰時軍事物資運輸的各項參數往往具有模糊不確定性,從而許多學者研究了帶模糊參數的VRP[8-13]。文獻[8]研究了帶模糊時間窗的多目標動態路徑優化問題,并利用遺傳算法進行求解;文獻[9]考慮了一類帶回路的模糊多目標車輛路徑優化問題,并提出了一種啟發式算法;文獻[10]針對車輛旅行時間、卸貨時間為模糊變量的車輛路徑問題,建立了基于可信性測度的模糊機會約束規劃模型;文獻[11]針對戰場軍事物資配送中帶硬時間窗VRP的模糊性,基于模糊可信性理論建立了多目標模糊期望值模型,并提出了一種改進的約束多目標粒子群優化算法;文獻[12] 分析了模糊模型和模糊方法,有效地解決了車輛容量約束條件下的運輸和VRP問題。但在戰時軍事物資運輸中,隨著戰場態勢的變換,運輸路徑上具有模糊性的參數較多,例如運輸時間、運輸費用和安全系數等參數實際上都是不確定的,具有一定的模糊性。針對這種具有特殊的多模糊約束優化問題,本文建立了模糊約束的多目標軍事物資運輸模型,并利用改進的多目標量子遺傳算法對該模型進行求解。
1 問題的描述及數學模型
1.1 多目標優化問題
多目標優化問題[14](multiple objective problem,MOP)可以描述為這樣一個極小化優化模型。
定義1MOP
Minf(x)={f1(x),f2(x),…,fm(x)}
s.t.hi(x)=0; ?i=1,2,…,p
gj(x)≤0; ?j=1,2,…,q
x=[x1,x2,…,xn]T∈X
式中,fi:Rn→R,?i=1,2,…,m為目標函數;約束條件hi,gj為定義在X上的函數:Rn→R。
MOP在優化過程中,一個可行解很難使所有的目標函數達到全局最優,因此怎樣定義解集是求解MOP的關鍵。本文采用的解集是Pareto解,其定義如下。
定義2Pareto支配
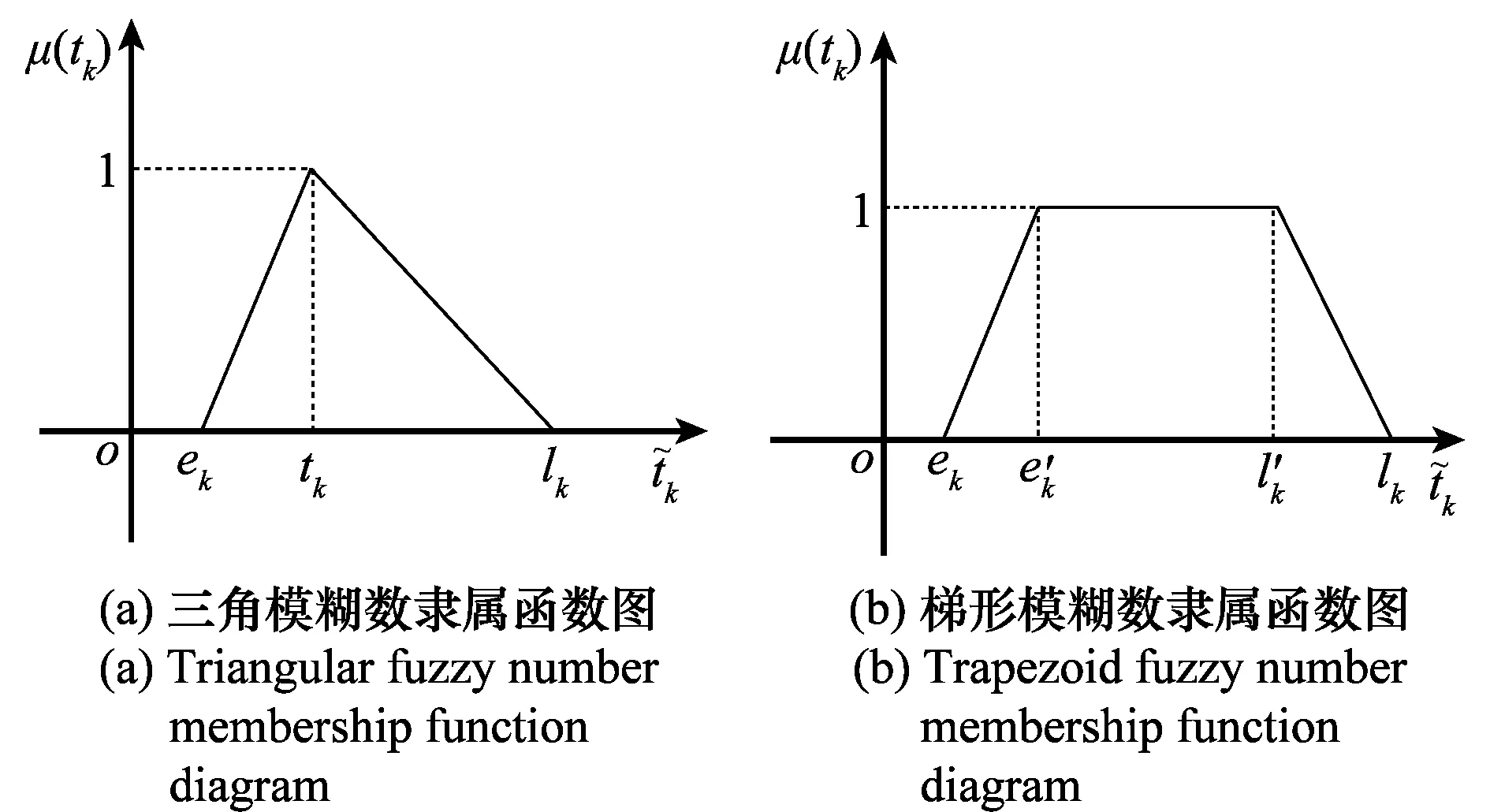
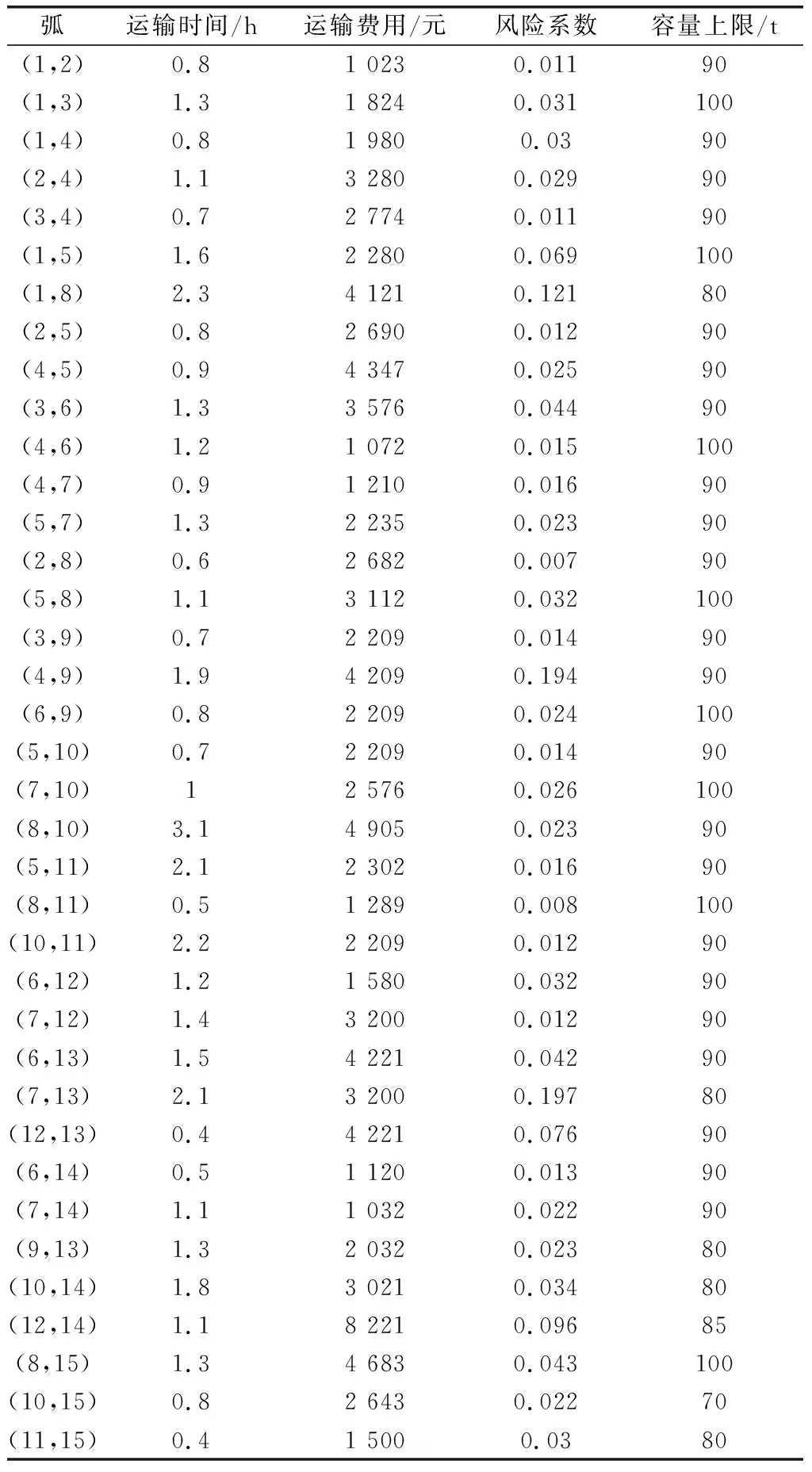
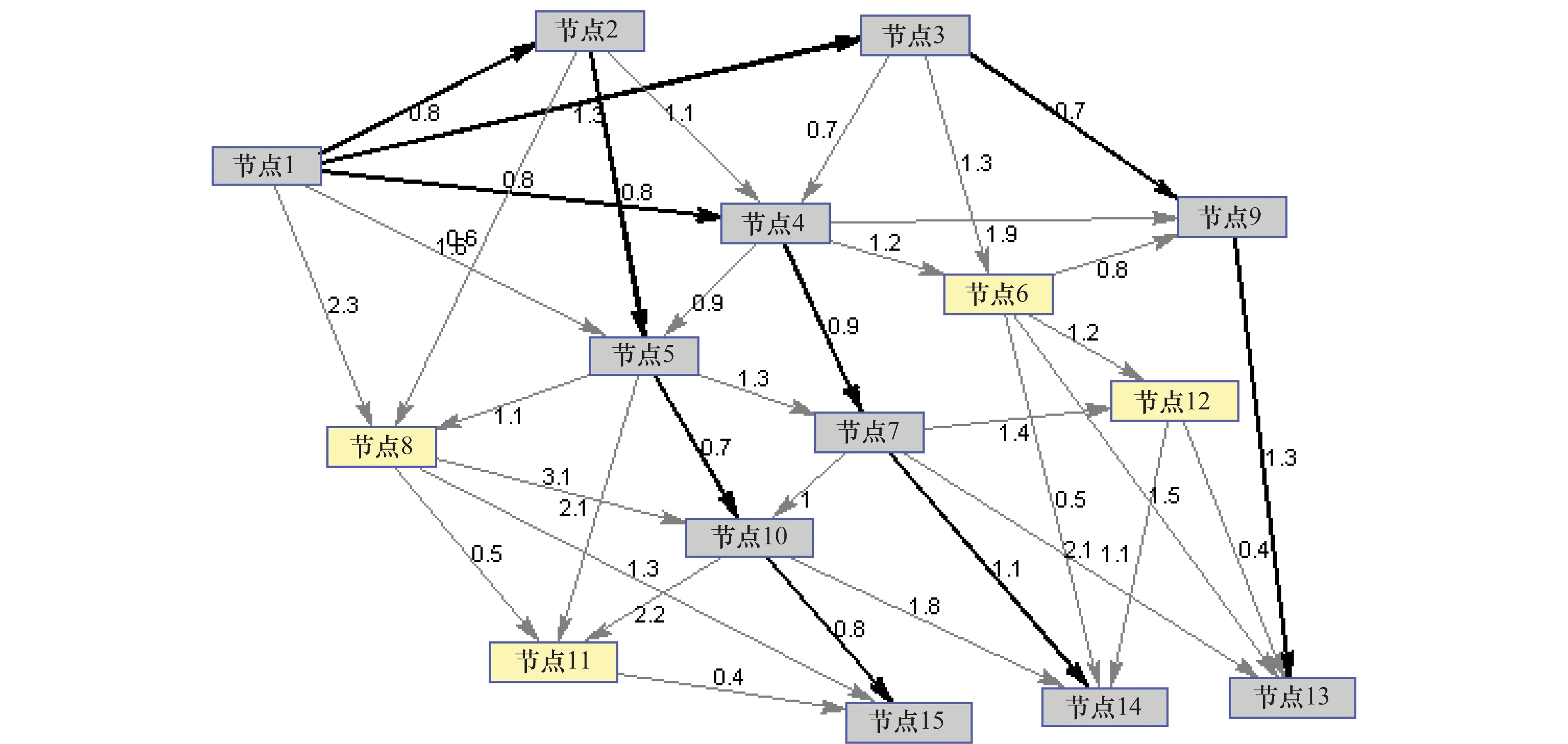
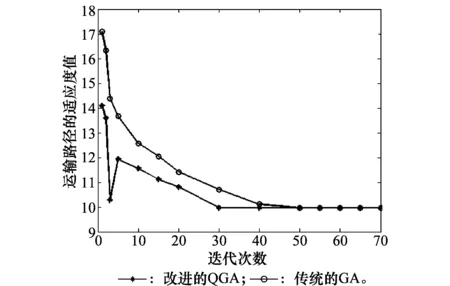
對于任意的可行解x,y,如果fi(x)≤fi(y),?i=1,2,…,m,且?j∈{1,2,…,m},使得fj(x) 定義3Pareto解 對于給定的MOP,可行解x為MOP的Pareto解,當且僅當不存在其他可行解y,使得ypx。 所有Pareto最優解的集合稱為Pareto最優解集,Pareto最優解集的像(目標函數值)稱為Pareto最優前沿。 帶模糊約束的多目標軍事物資配送路徑優化問題可以描述為由某一軍事物資配送中心v0向多個戰場配送物資的VRP,在滿足戰場需求、運輸路徑的容量限制等約束情況下,求運輸距離最短、費用最小、安全性能高等多個目標的優化問題。一般可以用運輸網絡G=(V,A,C)來表示,V表示網絡節點集,表示為 V={v0,v1,v2,…,vn,s1,s2,…,sm} 式中,v0表示網絡中的源點;S={s1,s2,…,sm}表示網絡中的匯點;{v1,v2,…,vn}為運輸路徑上的節點。A={eij|eij=(vi,vj),其中vi,vj∈V}∈V×V,表示網路的弧集。C={cij|(vi,vj)∈A},cij表示弧eij上所能承受的最大容量。網絡G=(V,A,C)實際上表示的是一個一對多的運輸保障網絡。 1.2.1 帶模糊時間窗的運輸時間最短的模型 由于戰場上軍事物資配送問題的特殊性,每個戰場(匯點)sk(k=1,2,…,m)往往要求在某一個特定的時間窗[ek,lk]被服務,否則將延誤戰機。這里我們將每一個戰場被服務時間窗口視為一個模糊數,模糊數是定義在實數域上的正規凸模糊集,最常用的模糊數為三角模糊數和梯形模糊數,這兩種形式都是根據其隸屬函數的幾何形狀命名的,如圖1所示。 圖1 三角模糊數和梯形模糊數隸屬函數圖Fig.1 Triangular fuzzy number and trapezoid fuzzy number membership function diagram 式中,目標函數越大,說明整個戰場軍事物資保障越及時,約束條件反映了每個戰場必須在固定的時間窗口內接收到物資。 事實上,還可以根據戰時每一個戰場的戰略地位不同,對每一個戰場分配一個權值λk,這樣優化模型更改為 1.2.2 帶模糊約束的運輸費用最小模型 在經典的運輸問題中費用最小的優化模型為 但這只適用于靜態的運輸網絡,戰時由于網絡路徑隨時都有可能遭到敵方不同程度的破壞,在運輸過程中受多種不確定因素的影響,而僅用一個確定的數額來刻畫每一條弧上的單位運輸費用不符合實際。為此,這里將單位運輸費用wij視為一個三角模糊數。基于該假設可得運輸物資費用最小模型為 1.2.3 帶模糊約束的風險最小模型 在運輸網絡中,弧eij受攻擊的概率(不安全系數)為qij(0≤qij≤1),則路徑P的風險值為 因此風險最小的目標函數為 1.2.4 模型建立 基于以上假設和分析,建立帶模糊約束的多目標軍事物資運輸路徑優化模型為 (1) (2) (3) (5) (6) (7) 0≤fij≤cij,?(vi,vj)∈A (8) (9) (10) (11) 其中,式(1)~式(3)是目標函數;式(4)為運輸過程中可行路徑的約束條件;式(5)為可行流的約束條件;式(6)為時間約束,要求可行路徑總的運輸時間必須在指定的時間區間[ek,lk]; 式(7)和式(8)表示流量需滿足戰場的物資需求和運輸道路的容量限制; 式(9)~式(11)為模糊數和參數的設置要求。 求解第1.2.3節建立的帶模糊約束的多目標軍事物資運輸路徑優化模型,重點是怎么將帶模糊約束的模型轉化為確定性模型。文獻[15-16]分別利用模糊運算和效用函數將模糊約束轉化為清晰的等價類來進行處理;文獻[17]利用隸屬函數,給出了三角模糊數取值區間的期望值和取值的期望值。本文受Jiménez的啟發,將帶模糊約束的模型轉化為確定性模型來求解。 從而運輸費用最小模型可調整為 同理,風險最小模型可修改為 綜上所述,帶模糊約束的多目標軍事物資配送問題可轉化為 (12) (13) (14) 其中約束條件依然為式(4)~式(11)。 通過第1節的處理,本文將帶模糊約束的多目標物資運輸問題轉化為一個帶不等式的確定性約束的多目標規劃問題。針對這個優化問題,將對傳統的量子遺傳算法(quantum genetic algorithm,QGA)進行改進來求解。事實上,目前很多學者利用QGA 來求解物資運輸路徑優化問題[18-19]。QGA利用量子計算中的量子比特和量子態疊加等概念和理論[20],將染色體的編碼用量子比特的概率幅來表示,使得一個量子比特染色體可以同時表示多個狀態,能以較小的種群表示較多的可行解。然后依據當前最優染色體的個體信息,利用量子旋轉門對染色體進行有效的更新,而不是采用傳統的交叉和變異的操作。本文對傳統的QGA算法進行改進,在算法中引入非支配排序和小生境密度,對種群中的個體進行前沿非劣分級,并采用精英保留策略,使得較優的個體能夠保存下來,這樣能夠有效地提高算法的尋優效率。 在經典計算中,采用0和1二進制表示信息,通常稱其為比特。在量子計算中,采用|0〉和|1〉表示微觀粒子的兩種基本狀態,稱其為量子比特。經典比特與量子比特之間的區別在于,量子比特的狀態除了|0〉和|1〉,還可以是其線性組合,通常稱為疊加態,即 |φ〉=α|0〉+β|1〉 式中,α和β是一對復常數,稱為量子態的概率幅,滿足|α|2+|β|2=1。 一個量子比特可同時包含0和1的信息,則m個量子比特可以表示2m個不同的狀態。含m個量子比特的個體j可表示為 式中,|αi|2+|βi|2=1;?i=1,2,…,m。 式中,L為染色體的基因位數;n為每個基因的量子比特數。 實際上在解碼中是將量子的不確定性轉化為一個確定個體的過程,其表示方式為二進制編碼,需進一步將其轉化成十進制數,這樣染色體的每個基因就對應成一個自然數,而每個自然數就對應于網絡中的一個節點。例如|011〉轉化為十進制數就是3,它代表網絡中節點3。染色體的每個基因都這樣處理后,整個染色體就表示成自然數編碼,其中自然數的順序就是運輸網絡路徑中節點的順序。 在解碼的過程中,有可能會出現非法解的情況,主要有兩種:編碼的重復和越界。因此,在解碼的過程中需要適當的修正,對于重復的編碼,直接去掉,例如染色體對應的路徑P=[012325],重復路徑為232,直接去掉修正后為P=[0125];對于越界的編碼,則在依概率選取量子態時去掉越界的量子態即可。如果經過修正后得到的解不滿足約束條件則直接去掉。 通過第2.2節得到的每一個可行解都有3個評價指標:戰場的滿意度、運輸費用和安全性,為此本文采用非支配排序和小生境密度來評判解的優劣程度。 對于每一個可行解X都設有兩個參數Xrank和Xid,其中Xrank為非支配排序,將解分為0,1,…,n個等級,同一個等級非支配序相等,取值越低的解越優秀,例如Xrank 式中,V(X)表示個體X中的所有節點的集合;A(X)為個體X中的所有弧的集合;||表示集合的勢。不難看出,Xid越高的解,反映在運輸路徑上表示該路徑與同等解集F中其他路徑相似程度較高,即該運輸路徑上比較擁擠,反之則比較稀疏。 旋轉門的更新是量子進化算法的關鍵。本文設計的量子旋轉門為 從而旋轉角度為 (15) 種群中的個體可以根據適應度函數值的優劣來進行排序,為了使每一代優秀的個體能夠繼續保留下來,在迭代時將父代中較為優秀的個體保留下來直接進入子代。具體操作為: 在第t代父代種群Q(t)中,計算每個個體的適應度函數并進行優劣排序,然后根據種群規模確定一定數量的優秀個體用集合Γ(t)表示,再在Q(t)中隨機選取個體進行量子變異產生子代種群P(t),其中量子變異以量子旋轉門更新的方式進行。最后通過計算集合Z(t)=P(t)∪Γ(t)中個體的適應度函數進行排序,選取滿足種群個數的最優個體作為第t+1代父代種群Q(t+1)。 通過前面的討論和分析,設計本文算法的主要流程如下: 步驟2按照第2.3節的方法,計算種群Q(t)中每個個體的適應度函數并進行排序,選取適應度函數較優的個體記為Γ(t)。 步驟3對種群Q(t)中的每個個體按照第2.4節的方式進行量子變異得到種群P(t)。 步驟4令Z(t)=Γ(t)∪P(t);計算Z(t)中每個個體的適應度函數并排序,選取前N個個體作為新一代種群Q(t+1)。 步驟5若t 因本文所研究問題背景的特殊性,目前沒有統一的測試案例,為此選取文獻[22]中案例的運輸網絡來進行仿真實驗分析。將案例中運輸網絡的節點1設為源點,即配送中心,網絡中節點13,14,15設為匯點,即模擬為戰時的3個戰場。由于本文研究的是帶模糊約束的多目標路徑優化問題,因此在仿真時,需對運輸網絡中給定的參數進行修正,將運輸時間參數ti調整為三角模糊數(tij-0.1 rand,tij,tij+0.1 rand);運輸費用參數wij改為三角模糊數(wij-10 rand,wij,wij+10 rand);風險系數qij改為(qij-0.01 rand,qij,qij+0.01 rand)。然后采用第1.3節的處理方法,處理之后的數據如表1所示。3個匯點的模糊時間窗口參數如表2所示。 表1 軍事物資配送網絡G中各項權值參數Table 1 Weight parameters G of military material distribution network 表2 模糊時間窗口參數明細Table 2 Parameters of fuzzy time window 根據前面建立的數學模型和設計的算法,將運輸時間、運輸費用和安全性作為單目標進行優化,分別尋找5條較優的路徑作為初始種群,利用改進的QGA算法,用Matlab軟件編程仿真,迭代100次,得到節點1到節點13,14,15運輸最優的路徑如圖2所示。 圖2 最優運輸路徑Fig.2 Optimal transportation route 從圖2中可以看出節點1到節點13,14,15的最優運輸路徑分別為1→3→9→13,1→4→7→14和1→2→5→10→15,其中各運輸路徑的相關參數如表3所示。事實上因為每一個匯點都帶有模糊時間窗口的限制,所以運輸路徑的各項參數不一定是最優的。若不考慮模糊時間窗口的約束條件,只考慮運輸時間少、費用低和風險系數低的優化問題,則最優的運輸路徑方案及相關參數如表4所示。 表3 帶模糊時間窗口的最優運輸路徑及相關參數Table 3 Optimal transportation path and related parameters with fuzzy time windows 表4 不帶模糊時間窗口的最優運輸路徑及相關參數Table 4 Optimal transportation path and related parameters without fuzzy time windows 對比表3和表4不難發現,若不考慮匯點帶模糊時間窗口的約束條件,節點13的最優運輸路徑方案不受影響,而表4中節點14和節點15的最優運輸路徑為1→4→6→14和1→2→8→11→15,其實驗參數明顯比表3中節點14和節點15的最優運輸路徑1→4→7→14和1→2→5→10→15要好,但是正因為運輸時間少導致不滿足節點14和15的時間窗口約束,從而在算法中把這樣的路徑排除。 此外,將本文提出的改進的QGA與傳統的GA進行對比,雖然都能夠得到最優的運輸路徑,但本文提出算法的收斂性效果較好,如圖3所示。 圖3 適應度值比較Fig.3 Fitness comparison 本文針對戰場上帶模糊時間窗口、模糊運輸費用以及模糊運輸風險問題,建立了帶模糊約束問題的多目標運輸路徑優化模型,并利用改進的QGA對其進行求解。雖然多目標運輸路徑優化問題很難找到絕對最優的運輸方案,但仿真結果表明,將改進QGA算法用于求解該問題,決策者能夠有效地獲得最優的運輸方案以及最優的備用運輸路徑,根據仿真結果中的各項參數值自行擇優選擇運輸方案。本文提出的建模方法和算法能夠有效的解決帶模糊約束的運輸路徑優化問題。1.2 帶模糊約束的多目標軍事物資配送問題
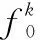
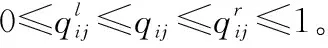
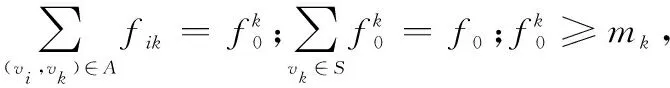

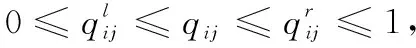
1.3 模型求解
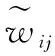
2 算法設計
2.1 量子位
2.2 量子比特編碼與解碼

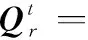
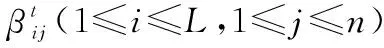
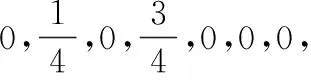
2.3 確定適應度函數
2.4 旋轉門的更新
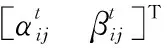
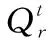
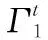
2.5 精英保留策略
2.6 算法流程

3 實例分析



4 結束語

