航天器面內機動規避最優脈沖分析

蘇 飛,劉 靜,張 耀,楊 旭,程昊文

(中國科學院國家天文臺,北京 100012)

0 引 言

航天事業的發展為地球外層空間帶來大量空間碎片,根據最新資料顯示,目前在軌10 cm以上空間碎片數量約2萬個,厘米級空間碎片接近50萬個[1-4]。惡劣的空間環境對航天器的安全運行造成巨大威脅,機動規避是航天器躲避空間碎片的一種主動防護措施,受到航天機構和衛星運行商的廣泛關注[5-8]。

國內外學者對航天器機動規避問題進行了大量研究。基于碰撞概率的防撞規避機動方法精度高,文獻[9-11]研究了碰撞概率和推力的解析表達,結合航天器軌道控制分析規避機動問題;在此基礎上,文獻[12-14]推導了機動脈沖與碰撞概率的解析關系,通過拉格朗日乘子法得到固定脈沖的最優方向;文獻[15-17]基于概率計算模型,通過一維碰撞概率積分方法推導速度增量的最優解,并利用兩體軌道積分代替高精度軌道積分研究碰撞規避機動策略;文獻[18]將機動脈沖解耦,分步求解脈沖方向和脈沖大小,在碰撞概率降低到安全值的前提下得到最優的機動沖量。許多學者通過分析規避機動動力學模型,利用尋優方法獲取避碰策略,文獻[19]分析了基于遺傳算法的燃料消耗和機動時長,采用多目標優化求解碰撞規避機動策略;文獻[20]利用非線性規劃算法求解最小速度增量,得到最優的碰撞規避機動策略;文獻[21]對近圓軌道提出了可以快速得到推力三維解的解析方法,利用梯度搜索算法找到最優解。一些學者從實際應用出發,建立量化的分析模型,不通過尋優直接分析次優解得到規避機動策略,文獻[22]研究了衛星規避相關的軌道機動方式,結合碰撞風險建立了衛星規避方案量化分析方法;文獻[23]利用根數長期項分析了初始軌道根數與危險交會點的關系,研究了衛星沖量對交會點的影響;文獻[24]分析了高度規避、時間規避、正常軌控結合的空間目標碰撞規避策略;文獻[25-27]研究了執行機動導致的額外風險和燃料消耗對航天器任務的影響;文獻[28]在單次脈沖的基礎上,分析了多次脈沖規避空間碎片能使衛星回到原始的運行軌道,同時不改變衛星原始狀態。

然而多數已有成果在研究航天器機動規避時,通常將軌道攝動方程外推,并在交會點處采用數值法窮舉尋優,雖然一些研究分析了碰撞概率與機動脈沖的解析關系,但在建立聯系時通常利用高斯方程直接求解,計算量大且只能得到次優解。為了解決最優解問題,首先通過小偏差線性化等處理將高斯方程解析化,得到解析的軌道規避機動動力學模型,直接分析機動脈沖與航天器相對運動的線性關系。通過航天器位置協方差信息及交會平面的相對位置信息得到航天器危險交會的碰撞概率和交會距離,并建立與機動脈沖的解析關系,然后采用機動方向和機動大小分步求解的策略計算機動沖量,高效準確地求解不同時機下的最優面內脈沖。

1 機動規避動力學建模

1.1 系統描述及建模假設

利用航天器運動方程對初始狀態和狀態誤差分布的協方差矩陣外推,就能預判航天器在運行過程中是否遭遇危險交會,如果危險交會的瞬時碰撞概率或交會距離大于安全閾值,則航天器需要進行機動來規避風險,保證運行安全。

在航天器危險交會規避任務中,往往通過改變軌道形狀來躲避碎片,即機動力或機動脈沖約束在軌道面內,這主要是因為面內機動控制簡單,同時改變軌道方位對航天器任務影響較大。航天器危險交會示意圖如圖1所示。

圖1 航天器危險交會示意圖Fig.1 Illustration of dangerous rendezvous trajectory of spacecraft

建模過程做如下假設:

假設1作用于航天器上的脈沖為小量,航天器在機動脈沖的作用下,到達危險交會點的速度大小及方向不變;

假設2危險交會過程為短期交會,碰撞時刻兩航天器的速度為勻速直線運動;

假設3兩空間目標等效為已知半徑的球體,位置誤差橢球在相遇期間保持不變;

假設4重力場為理想中心力場,忽略大氣阻力、太陽光壓等攝動因素的影響,忽略航天器姿態誤差對脈沖方向的影響。

1.2 坐標系定義

相關動力學建模參照坐標系如圖2所示,其中OXYZ為偏心率矢量坐標系,其原點O位于地球質心,X軸與航天器偏心率矢量eo重合,Z軸垂直于航天器軌道平面,正方向與航天器角速度方向相同,Y軸由右手螺旋法則確定;sxyz為航天器軌道坐標系,其原點s位于航天器質心,x軸由地心指向航天器質心,z軸與Z軸平行且指向相同,y軸由右手螺旋法則確定,三軸單位矢量分別為ex、ey、ez。

圖2 建模參照坐標系Fig.2 Reference frame for dynamics modeling

1.3 機動動力學模型

如圖2所示,航天器在偏心率矢量坐標系的狀態矢量表示為

(1)

式中,eX和eY為偏心率矢量坐標系對應坐標軸的單位矢量;a為航天器軌道半長軸;E為航天器對應真近點角處的偏近點角;e為航天器軌道偏心率;r為航天器地心距;μ為萬有引力常數。

令E=Em,取慣性系內航天器機動點即真近點角θm處的狀態rm、vm代入式(1),求解方程式得

(2)

式中,‖‖符號表示對矢量求模,將式(2)代入式(1)得偏近點角為E處航天器的位置矢量r，表示為

(3)

結合高斯方程,沖量使航天器軌道產生的瞬時變化為

(4)

式中,Δvx、Δvy、Δvz分別為沖量在航天器軌道坐標系三軸上的分量;h、p分別為航天器變軌前的軌道角動量和軌道半通徑,表示為

(5)

將航天器的狀態量代入式(3),則航天器在機動點θm處機動前和機動后,運行到危險交會點的位置矢量r(Ec)、r′(Ec)分別表示為

(6)

(7)

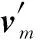
(8)

式中,Δrx、Δry分別為航天器在軌道系中相應坐標軸的位置變化。由于航天器機動后,其偏心率矢量坐標系繞Z軸轉動Δω,將式(6)、式(7)表示到機動前的偏心率矢量坐標系,則

Δr=A′r′(Ec)-Ar(Ec)

(9)

其中

(11)

(12)

(13)

(14)

為了推導方便同時減小因量級的巨大差異引起的仿真失真,進行歸一化處理,定義

(15)

(16)

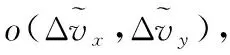
(17)

沿跡方向的距離變化考慮機動后,航天器運行相同相位條件下的時間差,基于文獻[22]對攝動參數的定義得

(18)

其中

(19)

(20)

(21)

將式(19)～式(21)代入式(18),分別在無攝動力存在攝動的情況積分,然后做差并泰勒展開,推導過程不再贅述,得沿跡方向的距離變化為

fx2(sinEc-sinEm)+fx3(cosEc-cosEm)+

fx4(sin 2Ec-sin 2Em)+fx5(cos 2Ec-cos 2Em)]+

fy2(sinEc-sinEm)+fy3(cosEc-cosEm)+

fy4(sin 2Ec-sin 2Em)+fy5(cos 2Ec-cos 2Em)]}

(22)

其中

(23)

從動力學模型可以看出,在機動脈沖為小量時,航天器機動導致的距離變化可以簡化為航天器軌道參數的解析表達,與外推模型相比可以大大節省計算時間,并能得到機動大小與距離變化的等式關系,有利于模型的物理分析和控制參數選取。

2 航天器危險交會分析

航天器危險交會過程中通常采用交會距離判定法或碰撞概率判定法來判斷發生碰撞的可能性。碰撞概率判定法適用于兩星的定位誤差較大且有累積效應時,交會距離判定法則適用于能實時測量兩星相對狀態。

2.1 交會距離

航天器運行時,設s(t)為t時刻航天器s-1與s-2的相對位置矢量,則任意時刻t+Δt兩個目標的相對位置矢量為

(24)

式中,vr=v1-v2,若t時刻兩目標間的距離最小,則有

(25)

根據式(25)得兩目標距離最小時,其相對位置矢量和相對速度矢量互相垂直。定義交會坐標系,其三軸單位矢量分別為

(26)

航天器相對運動方向平行于x軸,交會平面(b平面)定義為y-z平面,則航天器危險交會關系描述為兩航天器在b平面的交會距離,航天器軌道坐標系到交會坐標系的轉換矩陣為

(27)

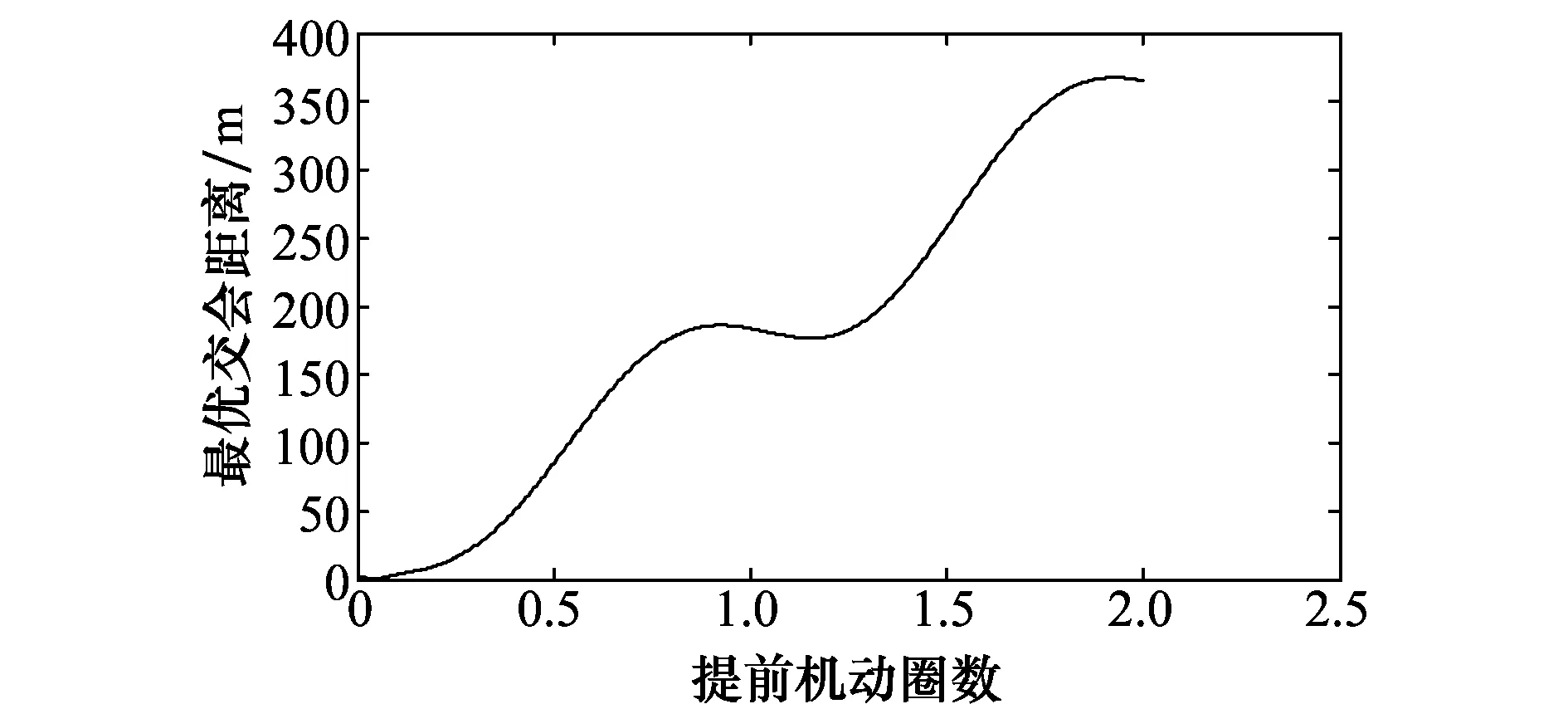
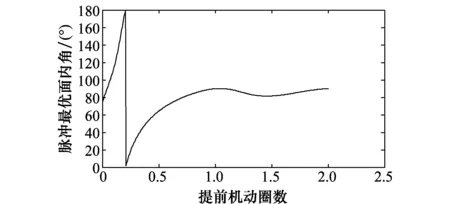
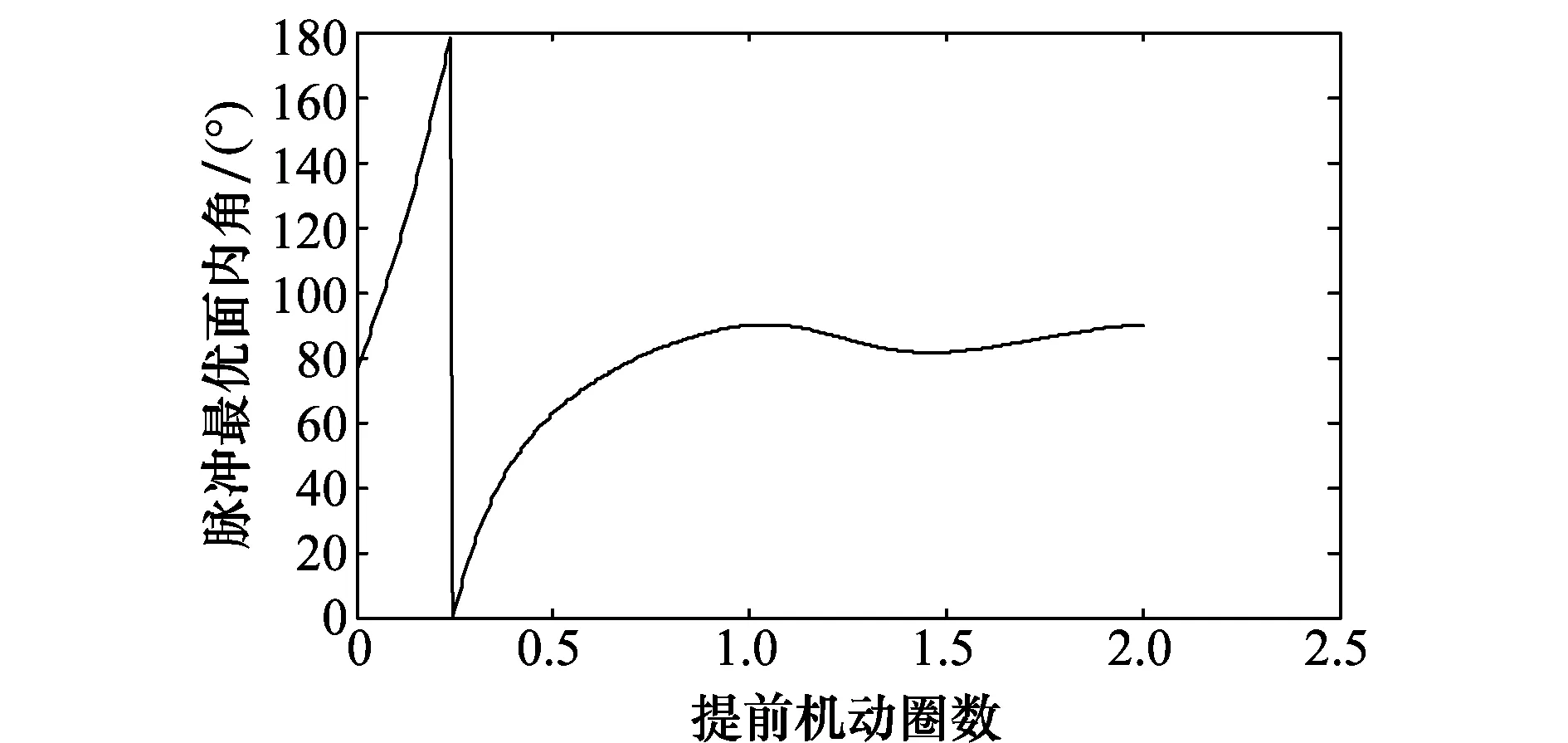
式中,α為危險交會點處s-2速度矢量v2在s-1軌道面投影與s-1速度矢量v1的夾角(-π<α<π),且v2×v1·eZ>0時為正;β為v2在航天器s-1軌道面投影與v2的夾角(-π/2<β<π/2),且v2·eZ>0時為正;B為v1與相對速度v1-v2的夾角(0

(28)

(29)

交會距離為

(30)

2.2 碰撞概率

航天器在運行過程中位置誤差服從3維正態分布,并可以通過分布中心和位置誤差協方差矩陣描述。此時航天器間交會的碰撞概率均可表示為

P=?Vf(x,y,z)dxdydz

(31)

式中,V為以一個航天器為圓心,兩個航天器包絡半徑之和ssum為半徑的球體;f(x,y,z)為高斯概率密度函數(probability density function，PDF),表示為

(32)

式中,se=(xbm,0,zbm)為b平面內兩航天器交會距離最小時的相對位置矢量;|C|為相對位置s誤差協方差矩陣C的行列式值,假設航天器交會時為勻速直線運動,則積分球變為圓柱,在誤差協方差矩陣中選取與相對位置信息有關的部分得

(33)

此時碰撞概率表示為圓域內的積分

(34)

文獻[6]提出一種不等方差PDF在圓域內積分問題的解決方法。通過將不等方差的等概率密度橢圓用與其面積相等的等概率密度圓代替,并用無窮級數表示二重積分,對式(34)簡化得到碰撞概率的解析表示，即

(35)

式中,u和v均為無量綱變量,表示為

(36)

(37)

3 最優規避分析

軌道維持條件下的交會距離及碰撞概率最優的規避機動計算采用兩步策略實現[16]:

步驟1通過求碰撞概率/交會距離對于機動方向的梯度確定機動速度方向。由于規避機動速度通常很小,可以將規避機動引起的交會點的航天器移動看成機動速度大小的線性函數,這樣碰撞概率/交會距離的梯度與機動大小就不相關,因此,最優的機動方向與機動大小可以獨立求解。

步驟2機動方向確定后,碰撞概率及交會距離即為機動大小的函數。求解滿足安全碰撞值和軌道維持要求的機動速度大小就是求解一個非線性方程。

(1)交會距離最優問題描述為

(38)

機動方向可以通過梯度矢量D得到

(39)

其中,D表示為

(40)

(41)

ρ2=fun(Ec,Em,e,φ)

(42)

當確定交會目標的Ec、Em、e,最優交會距離值所需要的機動脈沖速度方向即為式(43)的解。

(43)

(2) 同理,碰撞概率最優問題描述為

(44)

機動方向可以通過梯度矢量D′得到

(45)

其中,D′表示為

(46)

此時碰撞概率相關系數描述為

v=Fun(Ec,Em,e,φ)

(47)

當確定交會目標的Ec、Em、e,最優碰撞概率所需要的機動脈沖速度方向即為式(48)的解。

(48)

4 仿真分析及校驗

根據理論建模與分析的結果,建立航天器規避機動數值仿真模型和航天器危險交會分析模型。為了驗證所設計的規避機動策略的有效性,本小節利用美俄衛星碰撞事件為例進行仿真。Cosmos-2251和Iridium-33中,前者為俄羅斯的廢棄衛星沒有任何機動能力,后者為美國的在用通信衛星可以執行規避機動,選擇兩顆衛星碰撞前的各自最新的一組2行軌道根數(two line mean element，TLE)根數,利用簡化攝動預報模型(simplified general perturbations,SGP4)軌道預報模型,可知兩顆衛星交會時間(time of the closest approach，TCA)的參數如表1所示。

表1 美俄衛星碰撞交會幾何參數Table 1 Encounter geometry parameters of US & Russian satellite collision

其中,a、e、θ分別為Iridium-33的軌道半長軸、偏心率和真近點角,RI、RC分別為Iridium-33和Cosmos-2251的等效半徑,α為危險交會點處Cosmos-2251速度矢量在Iridium-33軌道面投影與Iridium-33速度矢量的夾角。β為投影與Cosmos-2251速度矢量夾角。

根據Cosmos-2251和Iridium-33的預報數據,相對位置s誤差協方差矩陣假設為對角協方差矩陣,其標準差在航天器相對運動切線方向為1 km,在b平面內的兩個正交方向上為100 m,此時在誤差協方差矩陣中與相對位置信息有關的部分[9]為

(49)

圖3是航天器機動規避時不同機動提前量下的最優交會距離,從圖3可得在提前量不是整數周期或不靠近整數周期時,提前機動時間越大,得到的最優交會距離越大;提前量為整數周期或在其附近時,最優交會距離回落,稍有減小。

圖3 不同機動提前量的最大交會距離(Δv=0.01 m/s)Fig.3 Maximum achievable miss distance under different maneuver opportunity (Δv=0.01 m/s)

航天器執行機動規避時,通常需要考慮軌道維持,即需要在避碰的同時完成軌道抬高,所以在仿真過程中,取脈沖方向與軌道系x軸夾角為0≤φ≤π,圖4是最優交會距離約束下航天器機動規避時不同機動提前量下的最優脈沖方向,從圖4得航天器規避提前量在0～0.2周期時,最優脈沖方向收斂至180°(0°),提前量超過約0.2周期后,最優脈沖方向收斂至90°附近。

圖4 不同機動提前量時的最優脈沖方向(Δv=0.01 m/s)Fig.4 Optimal direction of pulse under different maneuver opportunity (Δv=0.01 m/s)

圖5是航天器機動規避時不同機動提前量下的最優碰撞概率,與最優交會距離分析類似,從圖5可得在提前量不是整數周期或不靠近整數周期時,提前機動時間越大,得到的最優碰撞概率越小;提前量為整數周期或在其附近時,最優碰撞概率振蕩且稍有增大。分析式(44)可知,最優碰撞概率是交會平面內兩個距離量的二元二次函數,對兩式求偏導，得

(50)

從式(50)可知,最優碰撞概率的梯度是兩個距離量耦合,與誤差協方差矩陣相對位置信息式(49)對應,誤差協方差是表征兩個航天器位置誤差的累積,通過碰撞概率表示兩個航天器的危險交會具有實際意義。

圖5 不同機動提前量時的最優碰撞概率(Δv=0.01 m/s)Fig.5 Optimal achievable collision probability under different maneuver opportunity (Δv=0.01 m/s)

取脈沖方向與軌道系x軸夾角為0≤φ≤π,圖6是最優碰撞概率約束下航天器機動規避時不同機動提前量下的最優脈沖方向,從圖6得航天器規避提前量在0～0.25周期時,最優脈沖方向收斂至180°(0°),提前量超過約0.25周期后,最優脈沖方向收斂至90°附近。

圖6 不同機動提前量時的最優脈沖方向(Δv=0.01 m/s)Fig.6 Optimal direction of pulse under different maneuver opportunity (Δv=0.01 m/s)

圖7是航天器機動規避中,采用不同脈沖時不同機動提前量下的最優交會距離,從圖7可得相同提前機動時機下機動脈沖越大,最優的交會距離越大。

圖7 不同機動提前量時的最大交會距離 (不同脈沖)Fig.7 Maximum achievable miss distance under different maneuver opportunity (different impulsive)

圖8是最優交會距離約束下,航天器機動規避中,采用不同脈沖時不同機動提前量下的最優脈沖方向,從圖8得脈沖變化不影響最優機動方向。

圖8 不同機動提前量時的最優脈沖方向 (不同脈沖)Fig.8 Optimal direction of pulse under different maneuver opportunity (different impulsive)

圖9是航天器機動規避中,采用不同脈沖時不同機動提前量下的最優碰撞概率,從圖9可得相同提前機動時機下，機動脈沖越大,最優的碰撞概率越小。

圖9 不同機動提前量時的最優碰撞概率 (不同脈沖)Fig.9 Optimal achievable collision probability under different maneuver opportunity (different impulsive)

圖10是最優碰撞概率約束下,航天器機動規避中,采用不同脈沖時不同機動提前量下的最優脈沖方向,從圖10得脈沖變化不影響最優機動方向。

圖10 不同機動提前量時的最優脈沖方向 (不同脈沖)Fig.10 Optimal direction of pulse under different maneuver opportunity (different impulsive)

5 結 論

基于數理變化推導出解析的軌道規避機動動力學模型,建立了脈沖大小與機動位移的量化關系;利用航天器交會過程的協方差信息等得到碰撞概率和交會距離,通過代入機動位移分析了規避模型的優化目標函數;最后搭建仿真模型研究了航天器面內最優機動規避問題,為機動規避的工程問題提供支持。