基于Lasso含缺失數(shù)據(jù)的高斯圖模型的模型選擇

陳婷 長春工業(yè)大學數(shù)學與統(tǒng)計學院

一、引言

高斯圖模型是一種基于高斯分布假設的無向循環(huán)圖，也被稱為協(xié)方差模型選擇。Meinshausen and Bühlmann[1]使用Lasso的方法對高維稀疏圖進行協(xié)方差選擇。Yuan[2]將多元線性回歸和協(xié)方差逆陣中的元素聯(lián)系在一起，通過線性規(guī)劃的方式有效地求解高維協(xié)方差逆陣的估計。Dempster[3]提出了EM算法，Jiang[4]等提出了E-MS算法，并證明了其收斂性和相合性。

本文主要給出了含有缺失數(shù)據(jù)的情況下基于E-MS算法的高斯圖模型選擇的具體步驟即相應的理論推導。第二部分為符號說明；第三部分為理論推導；第四部分為模擬實驗；第五部分為結果分析。

二、符號說明

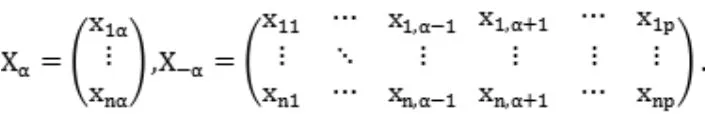
則領域選擇問題就轉化為求如下的Lasso回歸模型：

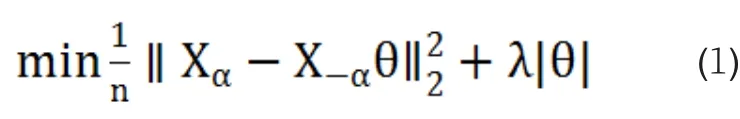
三、理論推導

E-MS的領域選擇算法原理：

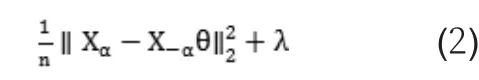
為了把上式最小化，采用坐標軸下降法。

當含有缺失數(shù)據(jù)時，采用E-MS算法，需要進行E步和MS步，在E步中，給出單調下降序列，然后利用BIC準則選最優(yōu)的。

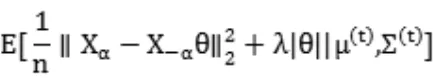
MS步要進行模型選擇最小化上式，用坐標軸下降法，易知期望中包含的項為：

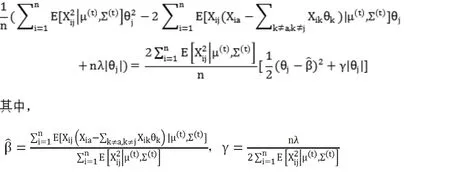
算法步驟如下：

輸入：觀測數(shù)據(jù)矩陣X

1.觀測樣本的分布，按一定的缺失率進行隨機缺失；

3.進行如下循環(huán)，直至收斂；

4.利用坐標軸下降法得到 的領域，根據(jù)完全數(shù)據(jù)陣Ex求一個圖結構G；

5.利用IPS算法求出圖結構的極大似然估計。

四、模擬實驗

p表示頂點個數(shù)，表示樣本容量，prec表示正確發(fā)現(xiàn)率，mcc表示馬修斯系數(shù),tpr表示特效度，tnr表示靈敏度，acc表示真值。在不同樣本下進行分析，運用R軟件，使用的軟件包是：mvtnorm包、MASS包、Matrix包。

表4 .1 缺失率在10%時進行模擬的結果

五、結果分析

在表4.1中可以看出，當p=10時，隨著n的個數(shù)的增大，prec的值在增大，說明正確發(fā)現(xiàn)率在提高，即估計出協(xié)方差中正確劃分有邊的個數(shù)與正確劃分邊的個數(shù)的比值在提升；tpr的值有所增大，即估計出的協(xié)方差中正確劃分有邊的個數(shù)同正確劃分有邊的個數(shù)與錯誤劃分無邊的個數(shù)的和的比值在提升；tnr的值有所增大，說明靈敏度在提高，即估計出的協(xié)方差中正確劃分無邊的個數(shù)同正確劃分無邊的個數(shù)與錯誤劃分無邊的個數(shù)的和的比值在提升；acc的值在增大，說明估計出的協(xié)方差中正確邊的個數(shù)也在逐漸變多。當p=15時，隨著n的個數(shù)的增大，prec、tpr、acc的值同p=10的情況一樣，但靈敏度的值在減小，這是在今后的研究中需要改進的地方。