數學課：讓思辨意識落地生根

☉江蘇省宿遷市鐘吾初級中學張揚

☉江南大學附屬實驗中學龐彥福

數學家哈爾莫斯說過：問題是數學的心臟.“提出一個問題往往比解決一個問題更為重要”，這是愛因斯坦的名言，他同時指出“因為解決一個問題也許只是一個數學上或實驗上的技巧問題，而提出新的問題、新的可能性，從新的角度看舊問題，卻需要創造性的想象力，而且標志著科學的真正進步.”《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）在第二部分“總目標”中指出：“運用數學的思維方式進行思考，增強發現和提出問題的能力、分析和解決問題的能力”，在第四部分“教學建議”中再次提出要引導和培養學生“不斷提高發現問題和提出問題的能力、分析問題和解決問題的能力”.的確，有了問題才能培養學生的思辨意識和思辨能力.《禮記·中庸》指出：“博學之，審問之，慎思之，明辨之，篤行之.”清代學者王夫之在《姜齋詩話·夕堂永日緒論外編二八》中指出：“故必極學問思辨之力……然后可以治天下國家.”因此，思辨是身處現代社會面對復雜問題時體現出來的睿智與能力.數學課該如何培養學生的思辨意識與思辨能力呢？現以筆者（江蘇省特級教師張揚）執教的一節初三一輪復習課“方程有解”為例與大家分享.

一、疑問，思辨意識孕育之時

問題1：解下列方程：

這是上課伊始出示的兩個解方程的例子，對于第（1）小題，化為整式方程，解得x=1，經檢驗x=1是增根，所以原方程無解；對于第（2）小題，去分母，得到2x-2（x-1）=1，化成一元一次方程的一般形式即得出0·x=-1，這樣一來，學生確實感到束手無策.對于學生而言，（1）比較容易理解，而（2）的結果并不常見.關于x的方程ax=b無解，則a、b應滿足什么條件呢？當然就是a=0且b≠0.

因為方程是含有未知數的等式，所以方程首先是等式.如果跳出方程來看等式問題，這類問題也可以這樣理解：由得出2x-2（x-1）=1，去括號、合并同類項后即為2=1，這顯然是不成立的，也就是說這個等式中的x無論取什么數值，都不可能使等式成立.譬如x=2時，左邊=2，右邊=1，當然不成立；再如x=-1時，左邊=-1，右邊=-，也不成立；當x=0時，左邊=-2，右邊=-1，亦不成立.

學生學習的過程中，問題是教師告知的還是他們自己通過探索發現的才是學與教的關鍵.常言道：“學起于思，思起于疑，疑起于問.”課堂提問是一種促進學生學習的方法，是一種教學手段，更是一種教學藝術.宋代教育家朱熹曾說：“讀書無疑者，須教有疑，有疑者，卻要無疑，到這里方是長進.”這對教學是很有啟發的，值得一線教師踐行.

二、思考，思辨意識發芽之始

問題2：解下列方程：

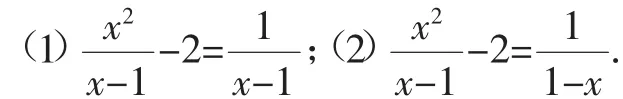
對于這組問題，去分母并整理后是一元二次方程，化簡并整理后，（1）為x2-2x+1=0，（2）為x2-2x+3=0.這兩個方程為什么無解呢？對于（1），學生容易存在兩方面的問題，其一是忘記檢驗，其二是認為一元二次方程x2-2x+1=0（分解因式為（x-1）2=0）的根只有一個x=1.其實一元二次方程x2-2x+1=0的根是兩個，只不過這兩個根是相等的，一般寫成x1=x2=1.關于方程（2），不少學生的潛意識是設法求出x2-2x+3=0的解.可是學生解著解著就感覺到有問題了，因為看似簡單的一元二次方程應該可以用因式分解法求解，但不行啊，x2-2x+3不好分解呀！用配方法或公式法才發現原來是△=b2-4ac搞的鬼！因為b2-4ac=4-12=-8＜0，該方程是沒有實數根的，也就是說，在實數范圍內不存在能使方程成立的數，比如，當x=-3時，左邊=，顯然不成立；當x=0時，左邊=-2，右邊=1，不成立；當x=2時，左邊=4-2=2，右邊=-1，也不成立.

細細想想，這兩個方程的無解是不一樣的，第（1）題是能夠求出未知數x的值，但其是增根，第（2）題是求不出來未知數x的值，所以這兩者的內涵是不一樣的.

變式：設計一個分式方程，使該方程化為整式方程時有兩個不等的實數解，而該分式方程無解.

變式問題是開放性問題，學生是不易很快想到的，但是，一旦明白了題意，問題就顯得簡單了.譬如：

通過這樣的嘗試與思考，學生對分式方程、一元二次方程的解法中蘊含的轉化思想會多一些了解，對分式方程的無解與關于x的一元二次方程ax2+bx+c=0的無解會理解得更深刻、更全面.

三、嘗試，思辨意識生長之根

對于問題3，如果缺少進一步的思考與嘗試，學生就無法體會到蘊含在思維過程中的分類討論的思想與方法.問題意識、思辨意識往往就體現在學習的過程中《.標準》明確指出：“數學活動經驗的積累是提高學生數學素養的重要標志.幫助學生積累數學活動經驗是數學教學的重要目標，是學生不斷經歷、體驗各種數學活動過程的結果.數學活動經驗需要在‘做’的過程和‘思考’的過程中積淀，是在數學學習活動過程中逐步積累的.”

四、體悟，思辨意識成為能力

有了對以上問題解決的經歷和經驗，學生很快會將問題4與問題2的（1）關聯起來，于是就出現了解題中的“秒殺”現象，得出答案x=1.當教師提醒同學們多想想時，細心的學生先將原方程化為：x2-2x+2-m=0，再分類討論.①當x=1是方程x2-2x+2-m=0的解時，得到m=1；②當△＜0，即△=（-2）2-4（2-m）＜0時，解得m＜1.即m=1或m＜1時，原方程無解.緊接著教師給出了變式1.

學生模仿問題4的解法，先由x=1得到m=±3，但是△＜0時出現m2＜9，有的學生沒能正確得到m的取值范圍.如果學生理解從m2＜9到m的取值范圍有困難，不妨借助數軸來完成，則可順利得出-3＜m＜3.

至此，學生則可體悟出方程無解的兩種情況，一是分式方程增根所產生的，二是一元二次方程的判別式△＜0導致方程無解.

當大部分學生還在解方程組時，已有學生明白了不需要解方程組，可以借助函數圖像解決.其實，關于x、y的方程組無解，就相當于拋物線y=x2-2x+3與直線y=-x+m沒有公共點.進一步品味方程無解，其往往是具有幾何意義的.

在本節課即將結束時，教師提出一個問題：這節課我們一起研究、討論的都是方程（組）無解的問題，為什么課題卻是“方程有解”呢？目的是引導學生進一步理解：無解只是方程的解的結果，在解答過程中體現出來的才是數學智慧和思辨能力.同時啟發學生在遇到學習或生活上的困難時，要擁有“方程有解”的意識，相信總有解決的方法，這種意識對教師而言也很重要，有助于促進教師由數學教學走進數學教育.

本節課作為初三一輪復習課，貫穿初中“數與代數”板塊三年所學的核心內容與知識“方程與函數”，方程知識是明線，函數知識是暗線.初三階段的一元一次方程、二元一次方程、可化為一元一次方程的分式方程、一元二次方程都被囊括其中；函數也涵蓋了所有初中階段的一次函數（含正比例函數）、反比例函數及二次函數.可謂知識線長，知識點多，知識源豐富.學習過程包含知識與認識、方法與想法、思想與感想、體驗與經驗的融合.使學生在投入思維的過程中體悟數學、理解數學、享受數學.明眼人都明白我們的教育真的應該少一些“消耗式的勤奮”，我們的教學應該少一些“低水平的重復”.

可能會有人認為本節課挖的太深了，偏離了考試的要求，偏離了教學的價值.什么是數學教學的價值呢？《標準》指出：“數學是人類文化的重要組成部分，數學素養是現代社會每一個公民應該具備的基本素養.作為促進學生全面發展教育的重要組成部分，數學教育既要使學生掌握現代生活和學習中所需要的數學知識與技能，更要發揮數學在培養人的思維能力和創新能力方面不可替代的作用.”培養人的基本素養，培養人的思維能力和創新能力難道不是數學教學的價值嗎？數學課程的核心任務就是思維的教學.思辨就是思考辨析，數學是思維的科學，思維是思辨的起點和基礎.思辨意識應該是思考的時候有在自己心中和自己辯論的意識.上課不僅僅是一種教學任務，就這節課來說，更多的是一種復習課的引領，一種教學的導向，引導一線教師用研究的方法進行備課，用研究的視野進行選題，用研究的方式進行教學，追求減負增效的課堂教學，倡導提高課堂效益的教學.本節課也是一種喚醒，是喚醒學生，也是喚醒教師和教育.

學習本課，進一步提醒學生學習數學或解題時應注意多想，解題時做到“先思后做”，解決一個問題務必做到厘清楚、想明白、寫規范.無論是舊課復習還是新授課，學生思維的參與是非常重要的.學生真正變成學習的主人，他們就是學習過程中的“領導者”“管理者”“創業者”，否則只能說是學習過程中的“打工者”“被動者”.學生學習數學要理解數學，其實，數學教師更應該深度理解數學，將數學知識的學術形態轉化為利于學生理解和消化的教育形態，是教師理解數學的重要體現.具備數學和教學雙重素養的教師，善于挖掘數學的教育價值，展示數學知識和方法的內在魅力，指導學生學會思考，學會學習.