“四基”蘊(yùn)于過程，“四能”寓于策略*
——以“圓周角（第1課時(shí)）”教學(xué)為例

☉重慶市重慶復(fù)旦中學(xué)丁慶彬

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》在教學(xué)建議中提出：“數(shù)學(xué)教學(xué)應(yīng)從學(xué)生實(shí)際出發(fā)，創(chuàng)設(shè)有助于學(xué)生自主學(xué)習(xí)的問題情境，引導(dǎo)學(xué)生通過實(shí)踐、思考、探索、交流等，獲得數(shù)學(xué)的基礎(chǔ)知識、基本技能、基本思想、基本活動經(jīng)驗(yàn)（以下簡稱‘四基’），使得學(xué)生主動地、富有個(gè)性地學(xué)習(xí)，不斷提高發(fā)現(xiàn)問題和提出問題、分析問題和解決問題的能力（以下簡稱‘四能’）.”可見，“四基”和“四能”均為數(shù)學(xué)教學(xué)的核心內(nèi)容.“四基”是在實(shí)踐、思考、探索、交流等教學(xué)環(huán)節(jié)中獲得的，應(yīng)體現(xiàn)過程性.“四能”的培養(yǎng)則依賴于教師的教學(xué)方法，應(yīng)體現(xiàn)策略性.數(shù)學(xué)教學(xué)只有兼顧過程性和策略性，才能使“四基”和“四能”得以落地.下面以義務(wù)教育人教版九年級上學(xué)期第二十四章“圓周角”第1課時(shí)的教學(xué)為例進(jìn)行說明.

一、概念“源”發(fā)生，自然流暢滲透思想

教材對圓周角的描述，只有一句話：“在圓中，還有另一類角，它的頂點(diǎn)在圓上，并且兩邊都與圓相交.”許多教師也基本上是開門見山給出概念，這樣處理教材略顯簡單，沒有對教材中“另一類角”進(jìn)行自然挖掘，使得概念的發(fā)生較為突然.為此，教師進(jìn)行如下設(shè)計(jì)：

師：同學(xué)們，我們知道圓心角是頂點(diǎn)在圓心的角，請同學(xué)們畫出一個(gè)圓心角∠AOB.保持角的兩邊與圓的兩個(gè)交點(diǎn)A、B不變，任意改變角的頂點(diǎn)，試一試還能畫出什么樣的角.

學(xué)生紛紛在剛才的圓中畫出各種各樣的角，教師匯總后利用多媒體呈現(xiàn)，如圖1.

師：請同學(xué)們觀察一下這些角，各有哪些特征？

生：有些角的頂點(diǎn)在圓的內(nèi)部，有的在圓上，有的在圓外.

師：是的，事實(shí)上無論頂點(diǎn)在圓內(nèi)、圓上還是圓外，都可以畫出無數(shù)個(gè)角.今天，我們重點(diǎn)學(xué)習(xí)比較特殊的一類角，它的頂點(diǎn)在圓周上，就是像∠ADB這樣的角.

教師引導(dǎo)學(xué)生進(jìn)一步觀察并歸納出圓周角的定義.

設(shè)計(jì)意圖：概念的生成改變了“開門見山”的方式，由復(fù)習(xí)切入，讓學(xué)生動手實(shí)踐，自然“發(fā)揮”，在此基礎(chǔ)上，引導(dǎo)學(xué)生進(jìn)一步觀察角的位置特征，教師及時(shí)引入“正題”，明確告訴學(xué)生要重點(diǎn)學(xué)習(xí)一類頂點(diǎn)在圓周上的角.這樣自然的引入，不僅讓學(xué)生在體驗(yàn)中領(lǐng)悟到概念發(fā)生的“源頭”，回應(yīng)了教材中“另一類角”的含義，同時(shí)滲透了“從一般到特殊”的數(shù)學(xué)思想方法.

二、新知“慢”探究，循序漸進(jìn)重視體驗(yàn)

本環(huán)節(jié)主要內(nèi)容是探究同弧所對圓周角和圓心角的關(guān)系及相關(guān)推論，既是本課時(shí)教學(xué)的重點(diǎn)，也是難點(diǎn).因此，在教學(xué)中不能簡單處理，更不能直截了當(dāng)給出結(jié)論，課堂節(jié)奏要“慢”下來，做到循序漸進(jìn)，讓學(xué)生獲得足夠的活動體驗(yàn)，感悟知識的來龍去脈.基于此，教師設(shè)計(jì)了如下三個(gè)探究活動.

探究1：一條弧所對圓周角和圓心角的關(guān)系.（圓周角定理）

該探究由五個(gè)小活動構(gòu)成.

畫一畫：引導(dǎo)學(xué)生探究同一條弧所對圓周角和圓心角在位置上會出現(xiàn)哪些不同的情況，并在圓中畫出相應(yīng)的圓周角，如圖2.

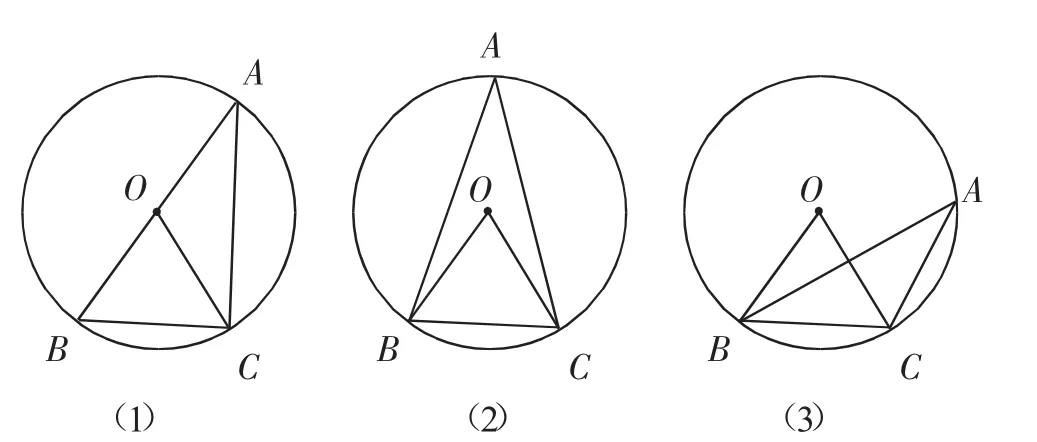
圖2

量一量：引導(dǎo)學(xué)生測量不同位置的圓周角和圓心角的度數(shù)，初步猜想它們之間的關(guān)系.

試一試：測量后的初步猜想“同弧所對圓周角是圓心角的一半”只是在三個(gè)不同圓周角的基礎(chǔ)上得到的，圓周角的個(gè)數(shù)并不具有普遍性，且人工測量會存在誤差.教師發(fā)現(xiàn)，在教材的正文旁邊有這樣一處旁白（如圖3），從而帶領(lǐng)學(xué)生運(yùn)用幾何畫板進(jìn)行動態(tài)展示（如圖4），發(fā)現(xiàn)無論圓周角和圓心角的位置和大小怎么變化，其比值始終是.

圖3

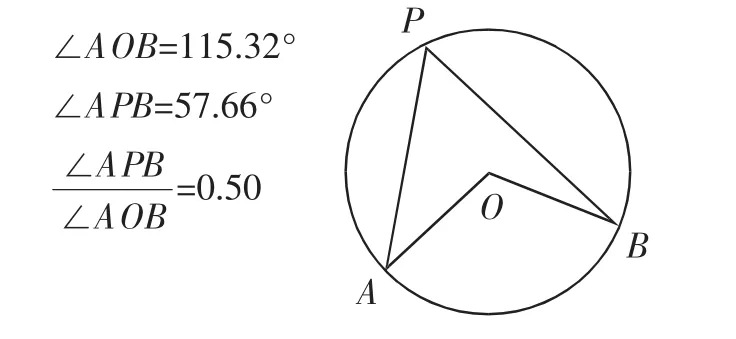
圖4

猜一猜：經(jīng)歷測量和計(jì)算機(jī)軟件的動態(tài)演示后，學(xué)生在感知“同弧所對圓周角和圓心角的關(guān)系”的基礎(chǔ)上，進(jìn)一步將猜想結(jié)論放大到“任意一條弧所對圓周角和圓心角的關(guān)系”上來.

證一證：經(jīng)過畫圖、觀察、猜想得到結(jié)論后，還需要用數(shù)學(xué)的語言加以證明.教師先引導(dǎo)學(xué)生一起給出圖2（1）的證明過程，并在教材旁白（如圖5）的提示中，對推出符號“?”進(jìn)行說明.對于另外兩種情況（圖2（2）、（3）），教師讓學(xué)生分組進(jìn)行證明，并讓一名學(xué)生在黑板上書寫了圖2（2）的證明過程，另兩名學(xué)生到講臺上分享了圖2（3）的兩種不同的證明思路.

圖5

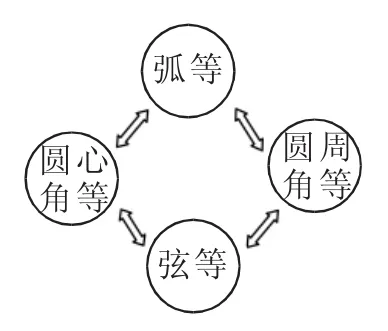
圖6

以上五個(gè)“一”活動后，教師進(jìn)行了歸納總結(jié)，提煉出“分類討論”和“化歸”（將圓周角問題化歸為三角形的外角問題來解決）的數(shù)學(xué)思想方法，并向?qū)W生強(qiáng)調(diào)：“連接半徑（或直徑）是圓中比較常見的輔助線.”

設(shè)計(jì)意圖：教育是慢的藝術(shù)，數(shù)學(xué)教育更是如此.圓周角定理的推導(dǎo)是一個(gè)循序漸進(jìn)的過程，在探究的過程中，節(jié)奏“慢”下，學(xué)生的思維才能“活”起來.無論是圓周角和圓心角的位置關(guān)系，還是數(shù)量關(guān)系，教師都沒有直接給出結(jié)論，而是讓學(xué)生自己動手操作，自主體驗(yàn)和觀察，并在教材旁白的提示下，恰當(dāng)使用了計(jì)算機(jī)技術(shù)輔助教學(xué)，使得教學(xué)過程流暢而嚴(yán)謹(jǐn).在證明定理時(shí)，教師十分重視數(shù)學(xué)思想的滲透、數(shù)學(xué)語言的表達(dá)和書寫的規(guī)范.

探究2：同弧或等弧所對圓周角的大小關(guān)系.（圓周角定理推論1）

在探究1的基礎(chǔ)上，借助已學(xué)過的“弧、弦、圓心角”之間的等價(jià)關(guān)系，學(xué)生完全能自己得到結(jié)論.因此，教師讓學(xué)生自主探究該推論，學(xué)生很快由弧相等得到圓心角相等，再根據(jù)“同弧所對圓周角是圓心角的一半”得到圓周角也相等的結(jié)論.教師并未就此結(jié)束，而是帶領(lǐng)學(xué)生對圓中的弧、弦、圓心角及圓周角四個(gè)常見元素之間的轉(zhuǎn)化關(guān)系進(jìn)行梳理，如圖6.

設(shè)計(jì)意圖：雖然由弧相等得到圓周角相等并不難，但教師并不是“就事論事”，更沒有“就此罷休”，而是引導(dǎo)學(xué)生在已有的元素（弧、弦、圓心角）之間的“知一得二”的基礎(chǔ)上進(jìn)一步梳理增加圓周角后的等價(jià)關(guān)系，從而得到“知一得三”的性質(zhì)結(jié)論，幫助學(xué)生建立新知識和舊知識之間的聯(lián)系，建構(gòu)完整的知識體系.

探究3：半圓（或直徑）所對圓周角為直角，90°的圓周角所對的弦為直徑.

教師改變了傳統(tǒng)的直接給出結(jié)論的做法，而是先讓學(xué)生對圓周角的取值范圍進(jìn)行探究，學(xué)生通過畫圖、觀察和探究得到圓周角的取值范圍為大于0°小于180°，教師又借助幾何畫板進(jìn)行動態(tài)展示，進(jìn)一步驗(yàn)證了學(xué)生探究的結(jié)論.之后，教師做了如下設(shè)計(jì)：

師：我們知道了圓周角的取值范圍，在這個(gè)范圍內(nèi)最為特殊的圓周角就是90°的圓周角，在演示的過程中，同學(xué)們發(fā)現(xiàn)當(dāng)圓弧滿足什么條件時(shí)，圓周角是90°？

生：當(dāng)圓弧與半圓重合時(shí)，所對圓周角為90°.

教師肯定學(xué)生的回答，并補(bǔ)充道：除了動態(tài)演示觀察，還可以通過半圓所對圓心角為180°得出“半圓（或直徑）所對圓周角為直角”這一命題，其逆命題也是成立的.

設(shè)計(jì)意圖：通過探究圓周角的取值范圍感知圓周角的大小變化，在變化的圓周角中進(jìn)一步聚焦到90°的圓周角，再次滲透從一般到特殊的數(shù)學(xué)思想.

三、應(yīng)用“巧”拓展，層層深入培養(yǎng)“四能”

經(jīng)過圓周角定理及相關(guān)推論的探究和學(xué)習(xí)，本課時(shí)的教學(xué)目標(biāo)基本達(dá)成，學(xué)生從中獲得了基礎(chǔ)知識、基本技能、基本思想和基本活動經(jīng)驗(yàn).但作為一堂幾何教學(xué)課，還應(yīng)該進(jìn)一步拓展和提升，教師設(shè)計(jì)了如下例題：

例如圖7（1），AB為⊙O的直徑，AB=10，∠A=30°，C為圓上一點(diǎn).

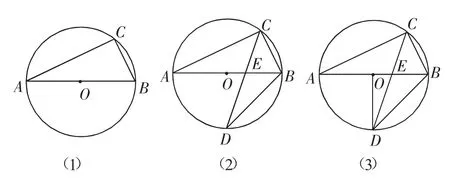
圖7

（1）求弦BC的長；

（2）如圖7（2），若CD為∠ACB的角平分線，交直徑AB于點(diǎn)E，交圓周于點(diǎn)D，求弦BD的長；

（3）如圖7（3），連接OD，求∠CDO的度數(shù)；

（4）在條件（1）（2）（3）的基礎(chǔ)上，你還能發(fā)現(xiàn)和提出哪些問題？嘗試解決.

學(xué)生運(yùn)用本節(jié)課所學(xué)知識基本上可以獨(dú)立完成前三個(gè)問題.第（4）問完全點(diǎn)燃了課堂氣氛，學(xué)生顯得十分興奮，各個(gè)小組紛紛提出自己的問題，教師適時(shí)引導(dǎo)，并讓小組之間相互解決所提問題.學(xué)生發(fā)現(xiàn)和提出的問題大概有以下三類：

類型1：求角的度數(shù)，如∠CEB、∠ACD、∠AEC等；

類型2：求線段的長度，如線段AE、CE、OE等；

類型3：求三角形的面積，如△CEB、△DEB、△ODE.

第一類求角度問題較為簡單，借助圓心角、圓周角的性質(zhì)及三角形內(nèi)角（或外角）可以很快解決.第二類求長度問題有一定難度，借助角平分線的性質(zhì)、勾股定理等知識解決，發(fā)現(xiàn)和提出該類問題的學(xué)生基本上能夠較為清晰地表達(dá)出解題思路.第三類問題在第二類問題上進(jìn)一步升華，但解決問題的思路是一致的，仍然需要先求出長度.解決問題的過程中，學(xué)生的方法也是多樣的，下面就以求線段AE的長度為例.

生1：利用角平分線的性質(zhì).

解析：如圖8（1），過點(diǎn)E分別作EG⊥AC于G，EH⊥BC于H.由角平分線易得EG=EH.

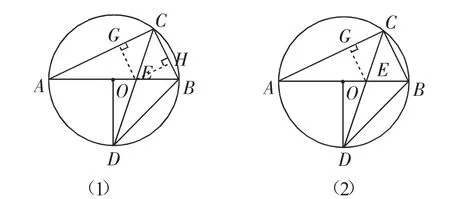
圖8

生2：利用直角三角形的特殊角.

解析：如圖8（2），過點(diǎn)E作EG⊥AC于G.

由題意易得∠GCE=45°，∠A=30°.△CEG、△AEG均為直角三角形.

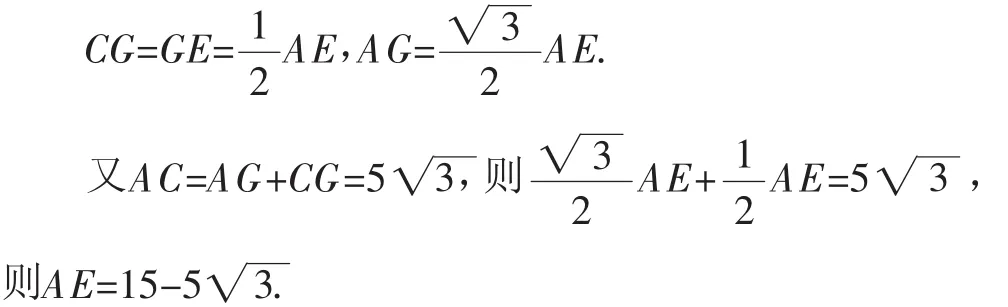
設(shè)計(jì)意圖：拓展不是無端增加難度，而是要體現(xiàn)知識的關(guān)聯(lián)和方法的融合.前三個(gè)問題的設(shè)置由易到難，層層深入，在變式練習(xí)中鞏固新知.第（4）小問的設(shè)計(jì)非常巧妙，既兼顧了本課時(shí)的內(nèi)容要求，又超越其知識范圍，實(shí)現(xiàn)了相關(guān)知識的深度融合；在思維能力上，不僅培養(yǎng)了學(xué)生分析問題和解決問題的能力，更注重發(fā)現(xiàn)和提出問題能力的培養(yǎng)，從而達(dá)到了“四能”并舉的教學(xué)目的.這種于“預(yù)設(shè)”中不“限設(shè)”、寓“四能”于無形的設(shè)計(jì)，充分體現(xiàn)了教學(xué)的策略性.

四、教學(xué)思考

本節(jié)課是一堂常態(tài)的幾何課，教師卻上出了不同尋常的味道，于“源”中追溯概念的發(fā)生，于“慢”中體驗(yàn)新知的關(guān)聯(lián)，于“巧”中兼顧“四能”的培養(yǎng)，為幾何教學(xué)提供了一種可借鑒的模式.同時(shí)體現(xiàn)出一種教學(xué)觀念：“‘四基’的獲得不能速成，應(yīng)充分體現(xiàn)在教學(xué)的全過程；‘四能’的培養(yǎng)不能一枝獨(dú)芳，應(yīng)于巧妙的教學(xué)策略中全面開花.”