公路橋梁車輛荷載與疲勞壽命的技術研究

魏德林

(中鐵十八局集團第一工程有限公司,廣東 清遠 511510)

全球都在積極研究橋梁疲勞問題。比如：英美國家系統規范了橋梁荷載,包括各種器件的疲勞程度、疲勞荷載等級設計、疲勞車輛模型等內容。國際對車輛疲勞荷載計算的方式包括：一種是關于荷載分布規律,具體根據交通產生的大量數據,整體分析典型車輛荷重以及對應頻率；另一種是與車輛有關的疲勞標準。我國擁有遼闊的土地面積,并在高原、平原、盆地等地廣泛進行分布,相應地會被氣候和地殼運動等因素進行影響,相應地產生了各種路橋體,形成不同的載重性。在這一狀況下,車輛也對各個區域的橋梁車輛疲勞荷載性能帶來較大的影響。我國研究人員通過分析交通整體行業,編制一些規范,但較少涉及公路橋梁的分析。現有的公路鋼橋規范缺乏合理性,具體是指鋼橋擁有較大規模,相應疲勞研究緩慢,這一前提下,鋼橋出現了顯著的安全性和可靠性問題。相較于國際疲勞理論分析,我國有關規范相對落后,現實價值明顯不足,公路橋梁車輛荷載僅對運營情況進行考慮,直接影響設計的精準度。為了改變這一現象,我國學者初步研究了公路橋梁車輛荷載與疲勞壽命的實踐性。

一、車輛荷載優化高斯建模方法

（一）高斯混合模型基本原理

在概率知識與數理統計中,高斯混合模型至關重要,其對若干個高斯函數進行了結合,也可以是一種稱之為狀態數具有持續特點的模型,進一步擬合預估分布空間數據的狀況。

利用高斯密度函數整體反映正態標準數據,普遍情況下,通常存在于數據空間的各個點不符合正態分布要求,此時通過融合不同的單一權重概率函數,也就是高斯模型成功擬合數據空間。基于理論角度分析,具備充足的混合數,多樣化的車型與不同車輛的載貨率形成十分復雜的車輛荷載模型。文獻[1]證明高斯混合模型逐步接近概率密度分布函數,在分布車輛荷載樣本概率中可以描述為高斯混合模型。這一模型采取了各種參數預估方式,其中普遍應用的是極大似然估計。其具體是在既定矢量訓練狀況下,獲取最理想的參數模型,從而得到最大似然模型函數。但普遍情況下,在參數和極大近似然函數之間擁有十分復雜的非線性關系,無法通過一般方式得出極大點,且會形成較大的計算量。

一個總體樣本中包含M個類型不同的個體樣本Xi=（X1,X2,...,XM）,Xi代表一維隨機變量,在樣本空間所占比例為Wi,子樣本形成具有獨立特點的變量,第i個子樣本與Pi（x）分布特點相符,進而形成有限混合模型,即:

車輛荷載與高斯混合分布相符。

（二）EM算法

EM算法對似然函數有效保證進而得到一個相對平衡點,憑借其高度穩定性與可用性得到十分廣泛的應用。有關研究認為,設計初始數值GMM對迭代算法速率進行了嚴重的影響,同時,該算法屬于一個對局部進行優化的搜索方法,一定程度產生局部性收斂,得到最佳解釋,這也是搜索結果與初始化參數不同的原因；一般采取隨機的初始簡單方式,不能獲得較好的使用效果,聯系前人的經驗教訓,將均值算法結果作為初始化參數。

根據樣本數據多權重和參數比值積極確定。對于多峰混合模型,訓練已知樣本的類標簽嚴重不足或不能觀測部分數據,被認定為典型不完全評價數據操作。由文獻[2]了解到EM算法能對典型性不完全數據似然問題科學處理。該算法主要憑借一個快速迭代的計算極大似然程序對數據實行估算,每次迭代劃分為兩個環節,EM算法的估算如下。

一維空間觀測數據Xi=（X1,X2,...,XM）參數極大似然估計表達式為：

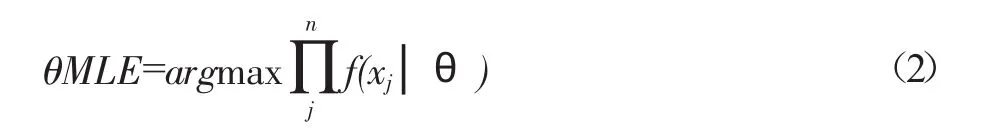
公式（2）提取數據的過程中,僅能獲取一部分參數數據,因此必須再一次構造完全數據類型。

強假設參數式方法為其創造了良好的性質：

（1）參數擁有非常有限的數量,一般比訓練樣例小,所以學習參數式方法相對比較簡單；

（2）參數化處置了估計分布,搜索最優參數的過程限制于一個無關訓練樣例數目的低緯度空間,防止高維狀況下出現維度災難問題；

（3）在合理假設的情況下,相對于非參數方法有效減少了所需樣本數量。

（三）高斯混合模型的優化

采取EM算法建立評估參數混合模型,并結合高斯分量數M實施,注意檢驗高斯分量數。在真實的狀況中,數據樣本包括未知的分布類型。嚴格劃分觀測樣本為多個模型數量,從而對數據樣本特性真實反映,模型也表現出復雜性。確定某一平衡點,在符合擬合模型精度前提下,提升混合模型自身便利性。對參數M數值合理明確時應注意模型的準確和便捷性,這也是模型改進的主要環節。

在信息統計中,已知數據觀測樣本十分復雜,故應建立衡量統計模型優良擬合準則,實現權衡所估計模型的復雜性及該模型擬合數據的優良性。通過AIC準則和BIC準則明確M參數,具體表達式為：

其中混合模型參數個數為m,樣本觀測向量長度為n,最大似然數值為 InL（x│M,wi,μσ2）。

二、標準疲勞車輛建模

（一）等效軸重

高斯混合模型真實體現分布公路車輛總重和軸重的概率,但在實際工程中直接運用,還必須有效的簡化模型。計算簡化是假定m輛等效模型車輛及統計同類車型對結構構件的疲勞損傷值基本相等。同時對車輛軸重和構件之間的應力變化科學設計,并制定線性數值關系,根據Miner準則及效力同等準則,等效軸重計算公式：

式中軸重隨機變量為Pi；f（Pi）是軸重的高斯混合概率模型。

（二）等效軸距

通過文獻數據分析了解所有車軸距分布的正態化,即:

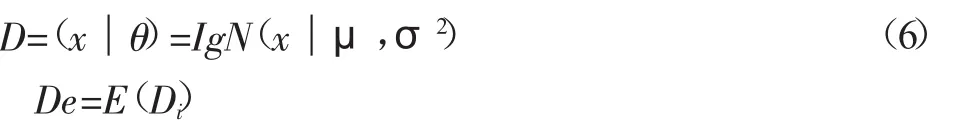
其中,等效軸距為De,統計軸距為Di。

（三）實例分析

1.車型和軸距

在統計交通荷載過程中總樣本為車流量,各種車輛類型代表任何一個由子樣本組成的總樣本。本文通過對南西路段承重數據動態監測,車輛以車軸數目為類型的劃分標準,劃分車輛具體包括C2、C3（A）、C3（B）、C4、C5、C6。由于橋梁通過普通輕型車輛時底緣鋼筋形成的疲勞應力與極限強度要求完全不符,故可以不考慮這部分車輛形成的疲勞貢獻。采取實時監測方法反映高速公路在一個月之內車輛荷載情況,總樣本數為27838輛。通過分析樣本可知,車流量明顯高于C3（A）、C3（B）、C5。在這一路段通過偶數類型車輛,地區特色十分顯著。結合對實際數據的統計,并結合公式計算各軸距形成的數據。

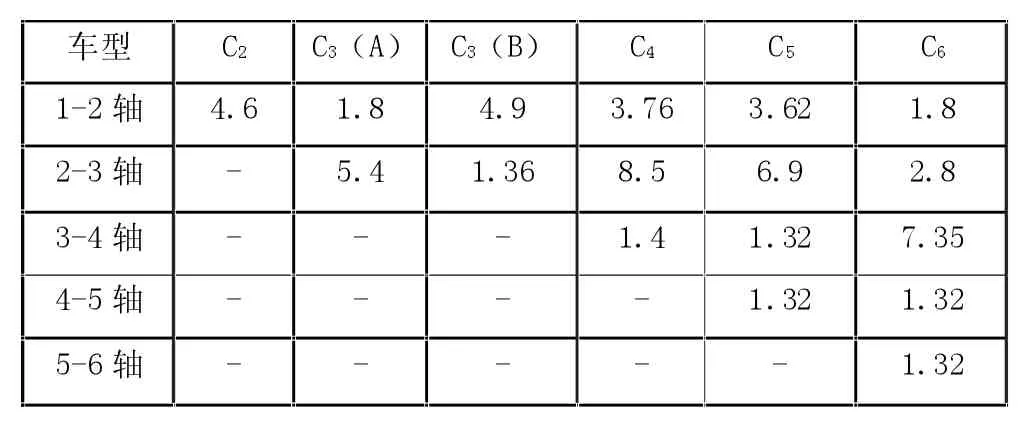
表1 典型車輛軸距統計（m）

2.軸重

比如建立C3（A）軸重荷載模型,對三軸軸重概率有效分析。通過計算可知,C3（A）一軸與二軸呈近似分布狀態,同時與三軸軸重出現了巨大的差別。具體原因是C3（A）前兩軸全部應用分布均勻的荷載。另外,C3（A）一軸與兩軸概率呈雙峰分布態勢,軸重具體包括10t、20t和40t。對C3（A）建模程序不斷重復,建立另外類型車輛軸重統計概率模型。對等效疲勞成功換算,得出疲勞車型在高速公路的相關標準。

表2 典型車型等效疲勞車輛軸重kN

三、等效疲勞車輛作用下梁橋疲勞壽命評估

（一）Miner線性累計疲勞損傷準則

Miner準則由于并不牽涉加載疲勞順序并對損傷疲勞數值進行準確計算,廣泛推廣應用在全國橋梁設計標準中。定義疲勞強度是通過循環使用疲勞應力數次后,材料由于疲勞產生斷裂。橫坐標在坐標軸上代表不斷循環應力的具體次數,縱坐標代表疲勞應力,通過完全擬合獲得材料曲線,表達式:

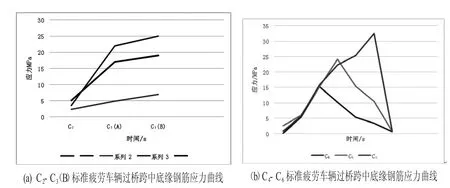
圖1 C2-C6標準疲勞車輛過橋跨中底緣鋼筋應力曲線

（二）高速某梁橋疲勞壽命評估

本文選擇WIM對某段高速公路T梁簡支工程作為研究對象。計算參考的有關參數：設計公路荷載Ⅰ級,計算跨徑39.5m,底緣鋼筋跨中一般牌號是HRB335。

通過有限元軟件對各個等效典型性疲勞車輛過橋程序整體分析,簡單繪制底緣跨中鋼筋應力曲線,見圖1。

采取雨流計數法準確計算車輛通過中橋梁底緣跨中鋼筋截面疲勞應力中螺紋鋼產生的疲勞強度,獲取通過橋梁的各類車型形成的鋼筋疲勞損傷值,見附表1。

在不考慮環境因素的情況下,在2015年11月梁橋通過車輛形成的疲勞損傷值5.5×10-5,未來交通量增加概率為5%,橋梁產生的疲勞壽命為89年。選擇單峰荷載模型、多峰簡潔荷載模型計算加載。由此可知,基于單峰荷載模型下橋梁產生82年疲勞損傷壽命,與多峰荷載模型的疲勞損傷時間對比前者相對較小,計算精度不佳。

四、結束語

社會經濟的迅速發展,逐步凸顯出公路橋梁的重要作用,但由于快速增加的交通量,人們也日益關注橋梁構件質量,特別是鋼構件的疲勞問題。公路橋梁近幾年由于疲勞破損經常發生意外事故,對人身財產帶來巨大的損失。為了不斷提升公路橋梁的安全性能,延長其應用壽命,本文聯系EM算法和信息統計學中AIC和BIC準則,提出了高斯混合建模方法,逐步提升了概率模型的準確度與便捷性,有利于公路車輛建立科學、高效的荷載概率模型。結合WIM調查得到的數據,可以利用高斯混合建模法對車輛通過橋梁分布軸重概率密度準確描述,得到典型車輛分布軸重概率函數。根據疲勞等效損傷準則,基于高速公路建立疲勞車輛等效模型,便于公路橋梁設置疲勞荷載以及評價疲勞壽命。評估了某簡支橋梁疲勞壽命,交通量設定為5%的增長率,橋梁疲勞壽命達到89年。在橋梁疲勞損傷壽命計算評價數值單峰荷載模型明顯小于多峰荷載模型。

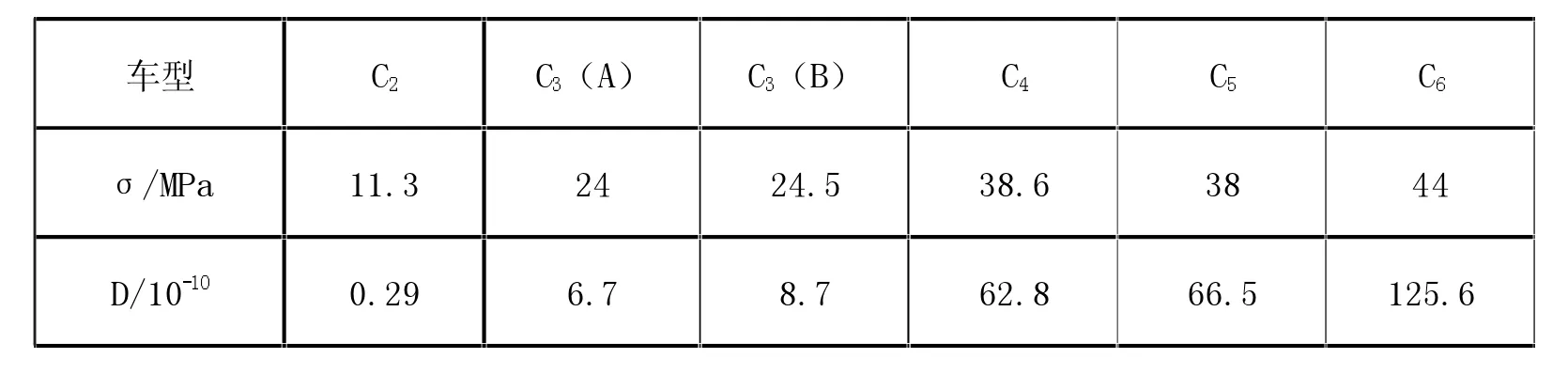
附表1 各種車型過橋對應的鋼筋疲勞損傷數值