提升建模素養 駕馭數學高考

安徽淮北師范大學數學科學學院 (235000)

張雨彤 張 昆

數學模型是一種運用數理邏輯方法和數學語言建構的數學模式，也是解決問題的重要途徑.通過建立數學模型，可以培養學生的應用意識，鍛煉學生從現實的生活背景中提煉相關的數量關系，提出問題，綜合與靈活地應用所學的數學知識、思想方法，用數學語言表達出來，選擇有效的方法和手段分析信息，進行獨立的思考、探索和研究，提出解決問題的思路，將現實問題轉化為數學問題，并加以解決.依據2017年新版《普通高中數學課程標準》建議，數學建模是對現實問題進行數學抽象，用數學語言表達問題、用數學方法構建模型解決問題的素養，這更是將數學建模素養放在了高中數學更為重要的地位上.所以，將數學與客觀實際問題聯系起來，通過實際問題抽象出數學表達式，并能夠聯系實際求解模型，應用模型，也一直是高考考查的熱點問題.

一、已知模型求解問題

根據解決的實際問題不同，數學模型多種多樣，包括概率模型、線性回歸模型、三角函數模型等等.然而本質上，數學模型就是系統的某種特征的本質的數學表達式(或是用數學術語對部分現實世界的描述).所以，在題目已給數學表達式的情況下，直接用求解函數的思路去思考求解數學表達式即可.

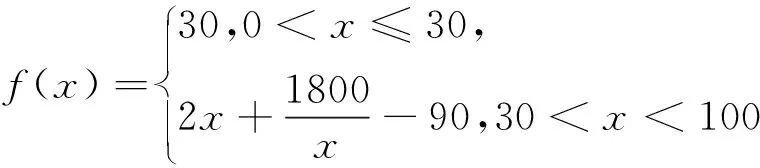
(1)當x在什么范圍內時，公交群體的人均通勤時間少于自駕群體的人均通勤時間？

(2)求該地上班族S的人均通勤時間g(x)的表達式；討論g(x)的單調性，并說明其實際意義.

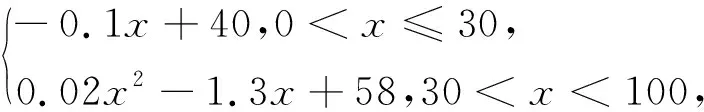
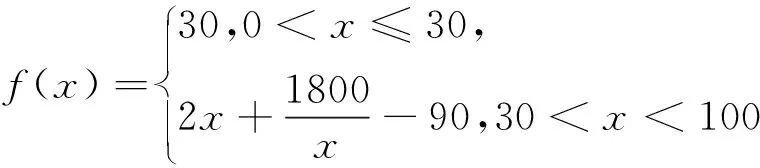
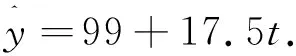
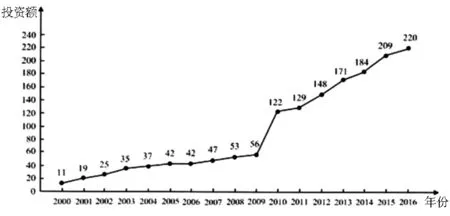
圖1

(1)分別利用這兩個模型，求該地區2018年的環境基礎設施投資額的預測值；

(2)你認為用哪個模型得到的預測值更可靠？并說明理由.

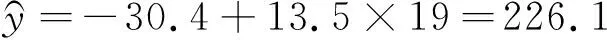
說明：高中階段，為了更好地將實際問題與數學問題相聯系，朝著建模邁出的第一步，就是將問題情境化，聯系數學模型與現實實際問題，這樣把數學情境化的嘗試可以讓數學更有現實關聯性且更有趣[2].每一個數學模型，它的實際意義可能有許許多多，就像之前學過的導數定義是實際問題中所有變化率在數學上的反映一樣，同一個數學表達式可以被賦予很多的現實意義，所以，在模型的預測值判斷上，一定會選擇用數學表達式計算出偏差較小的那個值.

二、依據信息建立模型

數學建模完全不同于其他數學分支，它不是“學”數學，而是“學著用”數學.數學建模是把數學和客觀實際問題聯系起來的紐帶.所以，在解高考題時，可以通過對題目中的信息進行整理與分析，找出其中的內在規律，抓住問題的主要矛盾，提出假設，經過抽象簡化，建立反映實際問題的數量關系式(數學模型)，然后運用數學的方法和技巧創新地分析和解決問題.

例3 (2018江蘇卷·17)某農場有一塊農田，如圖2所示，它的邊界由圓O的一段圓弧MPN(P為此圓弧的中點)和線段MN構成.已知圓O的半徑為40米，點P到MN的距離為50米，先規劃在此農田上修建兩個溫室大棚，大棚Ⅰ內的地塊形狀為矩形ABCD，大棚Ⅱ內的地塊形狀為△CDP，要求A，B均在線段MN上，C,D均在圓弧上，設OC與MN所成的角為θ.

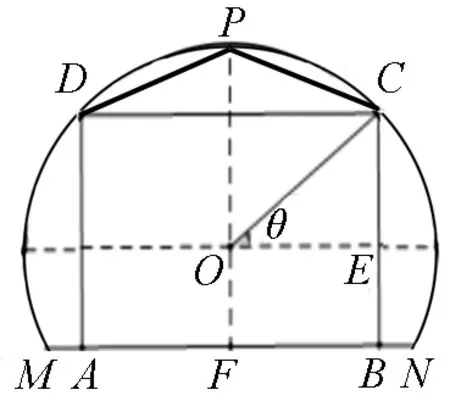
圖2

(1)用θ分別表示矩形ABCD和△CDP的面積，并確定sinθ的取值范圍；

(2)若大棚Ⅰ內種植甲種蔬菜，大棚Ⅱ內種植乙種蔬菜，且甲、乙兩種蔬菜的單位面積年產值之比為4:3，求當θ為何值時，能使甲、乙兩種蔬菜的年總產值最大.

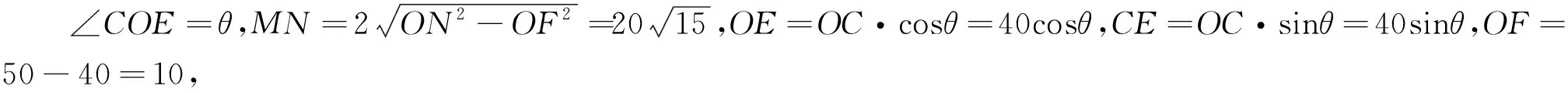
說明：當我們面臨實際問題時，一般情況下，對于學生而言，相對來說問題所提供的信息雜亂無章，不是輕而易舉就能理出頭緒的.要想真正解決實際問題，就必須通過意識機能、支點信息生成結構輪廓、記憶庫知識框架對比等一系列作用(如圖3所示)[3]，這種知識框架其實就是數學模型，找到了恰如其分的數量關系式(數學模型)來表示，然后再通過模型求解與分析，運用數學的方法和技巧創新地分析和解決問題.

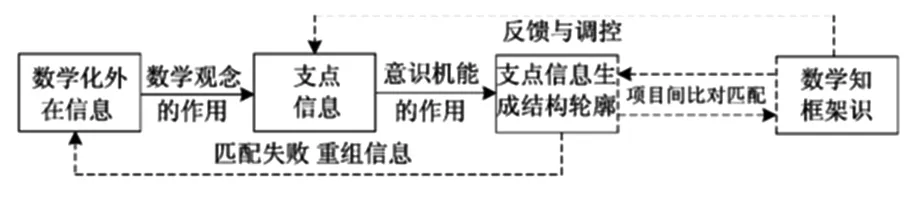
圖3

例4 (2018全國高考數學卷Ⅰ·20)一箱產品在交付用戶之前要對產品作檢驗，如檢驗出不合格品，則更換為合格品.檢驗時，先從這箱產品任取20件作檢驗，再根據檢驗結果決定是否對余下的所有產品作檢驗.設每件產品為不合格品的概率都為p，且各件產品是否為不合格品相互獨立.

(1)記20件產品中恰有2件不合格品的概率為f(p)，求f(p)的最大值點p0.

(2)現對一箱產品檢驗了20件，結果恰有2件不合格品，以(1)中確定的p0作為p的值.已知每件產品的檢驗費用為2元，若有不合格品進入用戶手中，則工廠要對每件不合格品支付25元的賠償費用.

(ⅰ)若不對該箱余下的產品作檢驗，這一箱產品的檢驗費用與賠償費用的和記為X，求EX；

(ⅱ)以檢驗費用與賠償費用和的期望值為決策依據，是否該對這箱余下的所有產品作檢驗？

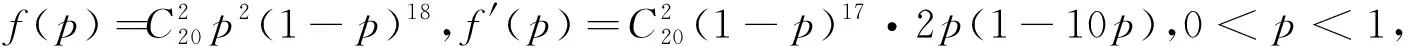
為二項分布，設一箱產品花的費用為X，則其分布列如下.

X025P910110

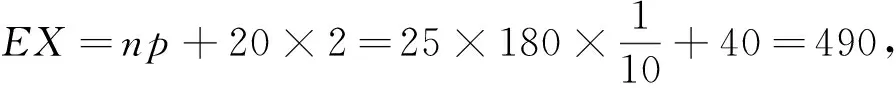
說明：概率模型只是數學模型中的一個類型，想要真正駕馭高考數學，必須要在頭腦中建立一個完整的數學建模體系.建立數學模型的一般步驟如下：(1)提出問題并用準確的數學語言加以表述；(2)分析各種因素，依據題目找出內在規律；(3)建立數學表達式(數學模型)；(4)按數學模型進行數學推導，得出有意義的數學結果；(5)對數學結論進行分析，若符合要求，可以將數學模型一般化和體系化，應用在數學預測等多種數學功能中.

三、結語

建模素養是考核數學應用的一項核心素養，它是通過將理論性的數學知識應用于現實世界中的過程，培養學生的數學思維能力，并且經由此，展示學生的實用性價值，在高考試題中滲透廣泛，要引起廣大數學教師的高度重視，并設法在教學設計中滲透這種數學建模思想意識，啟發學生形成具體的數學建模技能，積累數學建模的經驗.因此，在高三數學復習教學中，引導學生在一些實際問題上去發現問題，提出問題，建立數學模型求解，最后解決問題，可以幫助學生應對與駕馭數學高考.對此，我們高三數學教師應該思之再思，慎之又慎！