一道解三角形問題的多角度思考*

江蘇省海門中學 (226100)

李乃洋

解三角形問題是高中數學的基本題型，近年也出現了其與不等式相聯系的綜合問題.筆者最近在課上講評一道解三角形求范圍問題，針對學生的不同思考，略作整理，以探此類問題的不同角度認識.

題目已知ΔABC的三邊a,b,c依次成等差數列，且a2+b2+c2=21，則b的取值范圍是.

角度一：立足解三角形，利用正弦定理和余弦定理進行邊角轉化

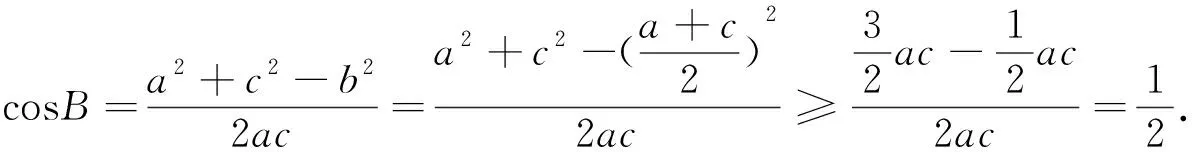
反思：解法1中利用了角B的范圍(有界性)得到邊的關系解不等式求得b范圍，但也有學生指出如何確定cosB<1是否擴大了角B的范圍從而影響計算結果.

角度二：利用等差數列構造消元

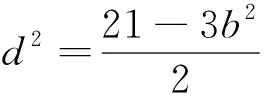
角度三：利用函數與方程思想轉化為方程有解來計算

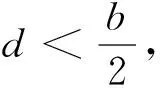
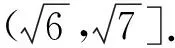
反思：方法3很好的體現了數學轉化思想，將幾何問題劃歸為代數(方程)問題，此方法可以理解為判別式法求解最值的延伸.

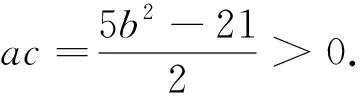
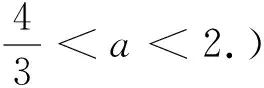
角度四:巧用均值不等式放縮

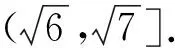
反思：利用不等式可以靈活產生不等關系，但是弊端是有時所求范圍不精確，更多是借用不等式比較大小或研究最值問題.

角度五：基于曲線與方程轉化為非線性規劃問題

因為a+c=2b,a2+c2=21-b2，消去b得5a2+5c2+2ac=84(*)(含a,c乘積項)，所以聯想此方程是某曲線的方程.

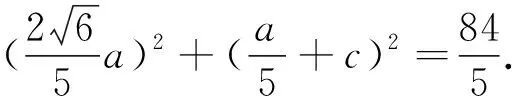
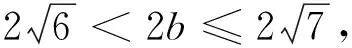
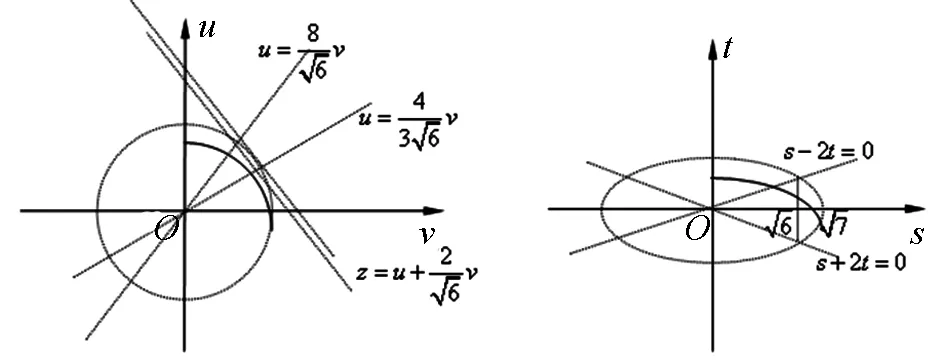
圖1 圖2

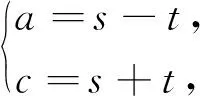
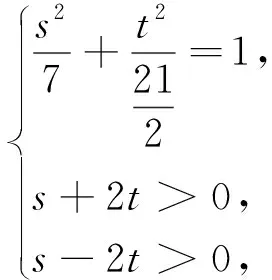
解法8：利用正交變換(旋轉變換)不改變曲線圖形特征來研究

角度六：對目標函數平方消元

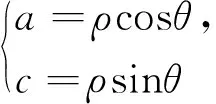
波利亞在其《怎樣解題》中提到解題需要尋求有用的思路，“從不同的角度來考慮題目”，強調不同的細節，從不同的途徑反復考查同一細節，以不同的方式進行組合，從不同的角度來利用它們.“你可以嘗試尋找過去所獲知識之間的聯系”.試著想想過去類似情況下是什么幫助了你，試著在你考查過的過程中認出一些你熟悉的東西，試著在你認清的東西中發現一些有用的東西，這是對一個問題多角度認識的直觀體現.