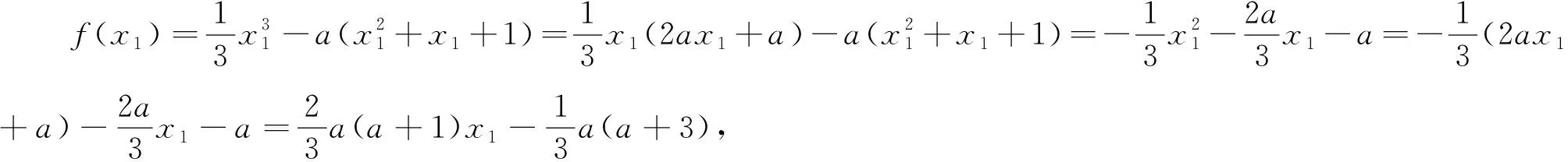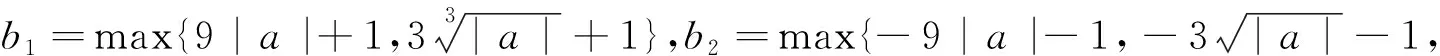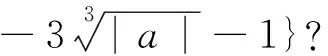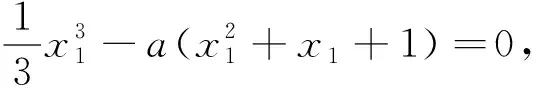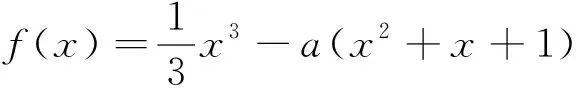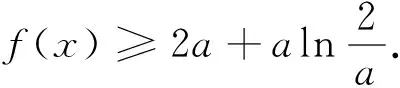高考導數壓軸題的那“點”事

廣東省廣州市真光中學 (510380)

黃林盛

核心素養下的高考對學生的綜合素養的提出了新要求，函數零點問題是高中數學考察學生綜合素養的很好途徑，主要體現在基本初等函數的圖像，滲透著轉化、化歸、數形結合、函數與方程等思想方法，在培養思維的靈活性、創造性等方面起到了積極的作用.近幾年的數學高考中頻頻出現函數零點存在的問題，其形式逐漸多樣化，難點在于函數零點所在區間內的取點問題.本文將以兩道高考題以例，闡述函數零點所在區間內應如何取點的基本方法.

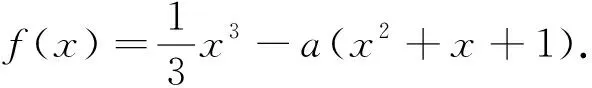
(1)若a=3，求f(x)的單調區間；

(2)證明：f(x)只有一個零點.

解：(1)略；

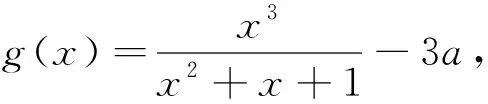
綜上，f(x)只有一個零點．

評析：如何思考到取3a-1,3a+1？

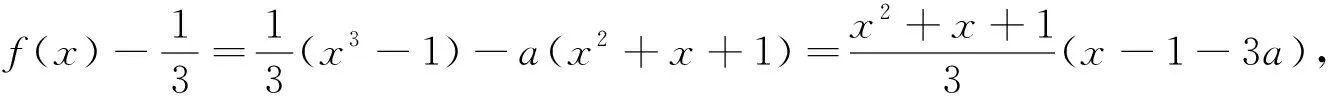
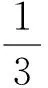
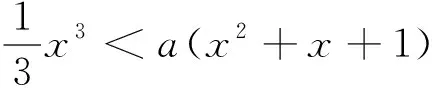
方法二：f′(x)=x2-a(2x+1)=x2-2ax-a,

①當△=4a2+4a≤0即-1≤a≤0時，f′(x)≥0恒成立，且等號僅在a=-1或0，且x=a時取得，所以f(x)在R上單調遞增.

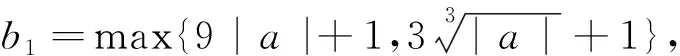
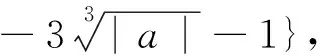
②當△=4a2+4a≥0即a<-1或a>0時，x2-2ax-a=0有兩個不等實根，不妨設為x1,x2(x1

綜上所述，f(x)只有一個零點.

評析:如何取得零點區間為(-3|m|-1,|m|+1)呢？

思路2：由g(t)=t3+t2+t-m可得，試點，g(0)=-m，g(-1)=1-m，g(1)=3-m，g(m)=m3+m2=m2(m+1),g(2m)=8m3+4m2+m=m(8m2+4m+1)，g(-m)=-m3+m2-2m=

-m(m2-m+2),g(-2m)=-8m3+4m2-3m=

-m(8m2-4m+3)，因為8m2+4m+1>0，m2-m+2>0，8m2-4m+3>0都恒成立，即有

g(2m)g(-m)<0,g(2m)g(-2m)<0.

試題呈現2 (2015年高考全國Ⅰ卷文科數學第21題)設函數f(x)=e2x-alnx.

(1)討論f(x)的導函數f′(x)的零點的個數;

當a≤0時，f′(x)>0，f′(x)沒有零點；

通過以上探究過程，可以總結零點區間端點選取的一般步驟：

步驟1：先分析當x→∞或x→a時，f(x)的符號，確定影響符號的關鍵項，然后通過等價轉化使得y=f(x)各項均為基本初等函數;

步驟2：由于放縮的需要，有時候需適當縮小零點區間端點所在區間，一般說來，若區間為(a,+∞)(a<0)或(-∞,a)(a>0)型，通常取(0,+∞))或(-∞,0)型，對于區間為(a,b)，型，區間通常可取(a,b′)，ab′>0型;

步驟3：一般來說，在不影響決定函數符號的前提下，常常要用到不等式或轉化成求某個函數在區間上的最值問題進行放縮，最終得到一個含參的可解不等式即可解出區間端點.

常用的放縮公式：

第一組：對數放縮

(放縮成一次函數)lnx≤x-1，lnx

第二組：指數放縮

(放縮成一次函數)ex≥x+1，ex>x，ex≥ex;

第三組：指對放縮

ex-lnx≥(x+1)-(x-1)=2.

第四組：三角函數放縮

第五組：以直線y=x-1為切線的函數