探高考題解法 談數(shù)學核心素養(yǎng)之計算能力培養(yǎng)

北京市第八十中學 (100102)

孫世林

2018年北京高考文科20題是一道解析幾何考題，綜合性強，能力要求高，全面深入地考查了解析幾何的知識本質(zhì)，同時也很好地體現(xiàn)了對數(shù)學核心素養(yǎng)之數(shù)學運算的考查；在高考中考生雖然解題思路較為清晰，但考生卻普遍失分較多，究其原因主要是數(shù)學運算的問題，解析幾何的知識本質(zhì)是用代數(shù)的方法研究幾何問題，所以運算能力成為了解決解析幾何問題的必備能力，下面通過2018年北京高考文科20題解法的探究，談?wù)勗诮忸}過程中如何把握代數(shù)運算，完善解題過程.

一、考題再現(xiàn)

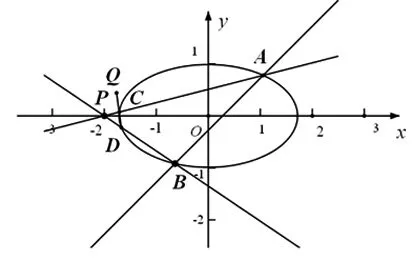
圖1

(1)求橢圓M的方程；

(2)若k=1，求|AB|的最大值；

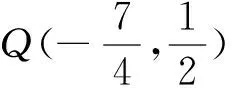
二、解法探究

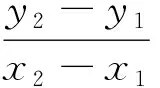
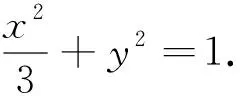
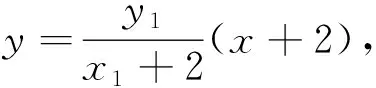
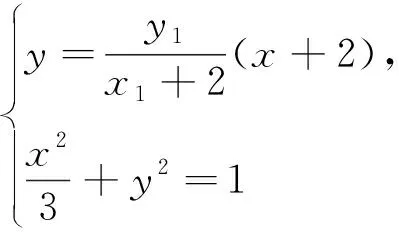
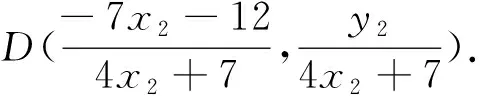
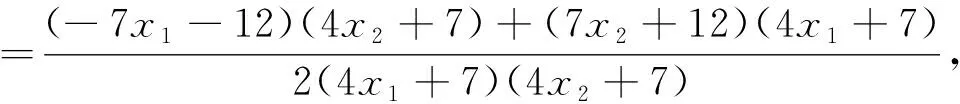
點評：解析幾何綜合問題常為在運動變化過程中探究某些不變的性質(zhì)與規(guī)律，對于這類運動變化問題，解題時要深入探究產(chǎn)生運動變化的根源，從產(chǎn)生運動變化的根源入手，自然快捷地解決此類問題.另外，解析幾何較歐氏幾何，最大的優(yōu)勢是把“運動變化引入幾何”，實現(xiàn)了“用坐標刻畫運動”；這種用代數(shù)手段來研究幾何問題的偉大構(gòu)想就是解析幾何的本質(zhì)，所以代數(shù)運算是解決解析幾何問題必須經(jīng)歷的過程，并且有的代數(shù)運算是相當繁瑣的，所以在平時的學習中要有意識強化代數(shù)運算，提高我們的計算能力.

分析2：在第三問中，可以理解為從點P(-2,0)作兩條直線分別與橢圓M依次交于C、A和D、B，求點C、D、Q共線時AB所在直線l的斜率，所以過點P(-2,0)作兩條直線是本題中的運動變化的根源，因此解決本題從PA、PB入手，設(shè)PA所在直線方程為y=k1(x+2)，PB所在直線方程為y=k2(x+2)，借助C、D、Q共線，尋求點A、B坐標的關(guān)系，從而求出直線AB的斜率.

解法2：(1)(2)略.

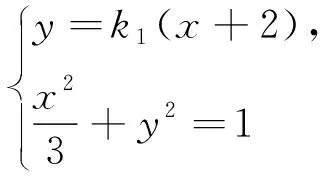
(1+3k1)x2+12k1x+12k1-3=0，則x1+x3=

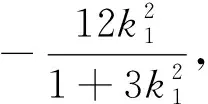
點評：解析幾何的核心方法是用代數(shù)的方法研究幾何問題，在解題過程中，首先要將文字信息、圖形條件進行對比互補，用恰當?shù)拇鷶?shù)語言描述幾何要素及其關(guān)系，將已知的幾何條件表示成代數(shù)形式，然后進行適當?shù)牡拇鷶?shù)運算得出代數(shù)結(jié)果，最后通過分析代數(shù)結(jié)果的幾何含義解決幾何問題，在這個過程中要經(jīng)歷文字信息、圖形特征和符號語言之間的多重轉(zhuǎn)換，但無論怎么轉(zhuǎn)化代數(shù)運算的結(jié)果的正確與否直接關(guān)系解題的成敗，所以重視代數(shù)計算，提高數(shù)學核心素養(yǎng)之計算能力的培養(yǎng)是解析幾何教學中必須引起重視的重要環(huán)節(jié)．

分析3：對于“直線與圓錐曲線的綜合問題”，通常將直線方程和曲線方程進行聯(lián)立，消元后得到一個一元二次方程，再結(jié)合韋達定理、根的判別式等來處理相關(guān)問題，這似乎成為了解決圓錐曲線綜合問題“通用”的解題策略，其本質(zhì)就是相關(guān)“點”是直線與圓錐曲線的“公共點”，從而轉(zhuǎn)化為方程組的解，借助方程組的解來探究題目中的幾何關(guān)系；但這種“通用”的解題策略有時會有較為繁瑣的解題過程，深入思考此種方法，可以直接將點的坐標代入圓錐曲線或直線方程，再借助“點坐標”這一代數(shù)形式下的運算實現(xiàn)對題目中幾何關(guān)系的探究，避免了解方程組的繁瑣，從而簡化運算.

解法3：(1)(2)略.

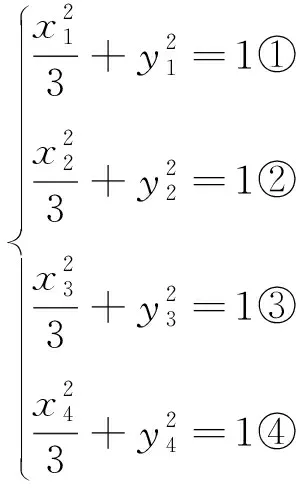
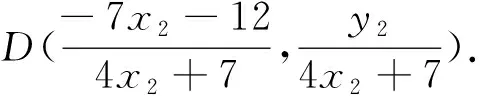
點評：此種解法避開了解決圓錐曲線綜合問題“通用”的“聯(lián)立方程、消元、韋達定理、根的判別式”解題策略，由于題目中相關(guān)的點是橢圓和直線的公共點，此種解法充分抓住了這些點的坐標滿足相應(yīng)的方程的特點，從而轉(zhuǎn)化為這些點坐標間滿足的關(guān)系，在尋求這些坐標間的“相關(guān)聯(lián)之處”，從而解決此題；此法很好地體現(xiàn)了解析幾何的本質(zhì)，即“用坐標刻畫運動，用代數(shù)方法來研究幾何問題”.

三、反思

圓錐曲線是一個幾何圖形，圓錐曲線問題中包含了一系列的幾何關(guān)系，怎樣才能更好地研究這些幾何圖形中的幾何關(guān)系，數(shù)學中引入了“解析法”，其核心是用代數(shù)的方法研究幾何.在解決解析幾何問題時，要借助平面直角坐標系，將平面內(nèi)的“點”與“數(shù)對”之間建立一一對應(yīng)的關(guān)系，要深入探究用什么樣的代數(shù)形式表示題目中的幾何關(guān)系，再通過對代數(shù)關(guān)系的研究，實現(xiàn)研究幾何圖形性質(zhì)的目的．

學習解析幾何的攔路虎之一就是代數(shù)變換的繁瑣、冗長，需要較強的運算能力.解題過程中，許多學生都是因為不能順利進行代數(shù)變換而導(dǎo)致失敗.而高中數(shù)學課程中明確提出應(yīng)注意提高學生的數(shù)學思維能力，這是數(shù)學教育的基本目標之一，其中運算求解、數(shù)據(jù)處理能力就是數(shù)學思維能力的具體體現(xiàn)，考綱中也明確提出了考查學生的運算求解能力和數(shù)據(jù)處理能力的具體要求.因此，教師不要將計算結(jié)果直接給出，在課堂上和復(fù)習中應(yīng)舍得花時間和學生同甘共苦經(jīng)歷計算的過程，向?qū)W生闡述每一步計算的算理，提醒學生注意每一個計算細節(jié)，區(qū)分不同參數(shù)的地位作用，教給學生重要的代數(shù)變換方法和必備的計算技巧，運算能力的提高是一個長久且螺旋式上升的過程，教師要注重對學生進行算法、算理的引導(dǎo)，教師要結(jié)合學生的實際有意識的設(shè)計一些開放性問題讓學生去探究，培養(yǎng)學生耐心細致的運算習慣，培養(yǎng)學生的意志力，教育學生要有信心、耐心、信心和恒心，同時引領(lǐng)學生根據(jù)有關(guān)“形”的特征盡量減少運算，充分利用定義、形的特征簡化運算，相信學生的運算能力一定能提升，使得學生解決解析幾何問題更加得心應(yīng)手.

解析幾何中涉及直線與圓錐曲線的綜合問題一直是高考、高校自主招生及各類競賽的熱點、難點、重點，尤其面對繁瑣的步驟及復(fù)雜的計算，往往令學生束手無策，甚至產(chǎn)生畏懼心理.在教學實踐中，學生往往真奔主題，強行求解，這樣不僅花費了大量寶貴時間，而且往往因為字母多、步驟繁、計算量大導(dǎo)致精神緊張、體力透支、推理出錯，出現(xiàn)絕大多數(shù)學生半途而廢甚至無功而返的尷尬局面.上述解法探究，重點在如何恰當利用題目中的幾何條件、如何優(yōu)化解題過程、怎樣細化代數(shù)運算的探究，特別是代數(shù)運算的關(guān)鍵環(huán)節(jié)的處理做了深入細致的分析，希望能給同學們的解題帶來幫助.