橢圓、雙曲線的一個性質及其應用

寧夏彭陽縣第一中學 (756599)

楊莉莉

在圓錐曲線的教學與學習中，我們容易得到橢圓、雙曲線的如下兩個性質：

圖1

圖2

性質2的證明同性質1.此略.

我們發現用這兩個性質求解橢圓、雙曲線涉及到中點弦、弦中點的問題，具有思路簡潔、計算量小的特點，下面舉例予以展示.

又a2-b2=9，所以得b2=9，a2=18.故選D.

例3 (2015新課標卷理20題)已知橢圓C:9x2+y2=m2(m>0)，直線l不過原點O且不平行于坐標軸，l與C有兩個交點A、B，線段AB的中點為M.

(1)證明：直線OM的斜率與直線l的斜率的乘積為定值；(2)略.

解:(1)的證明方法同性質1，得到直線OM的斜率與直線l的斜率的乘積為-9(定值).

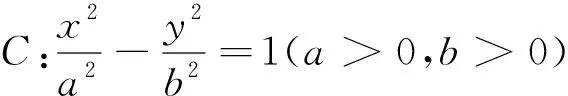
(1)求C的離心率；(2)略.

(1)求實數m的取值范圍；(2)略.

圖3

(1)求橢圓C的方程；

(2)求ΔABP的面積取得最大時直線l的方程.

在數學教學中，特別是數學解題教學中，我們要引導學生善于發現問題、總結規律、提煉結論，并會用新的結論簡潔的解答數學問題.