利用AM-GM不等式巧解2018課標Ⅰ卷理第16及20題
福建省南平市高級中學 (353000)
江智如 李壽濱
隨著2018年高考的結束,全國數學課標Ⅰ卷也掀開了神秘的面紗.縱觀課標Ⅰ文理全卷,試卷嚴格遵循考試大綱的要求,符合新課標的課程理念,有效地將數學文化與數學應用高度融合,充分考查考生的數學核心素養.試題結構穩中有變,難易適度,有較好的區分度,不僅有利于高校的人才選拔,又有利于高中數學教學與素質教育的順利開展,有效促進高中數學新課程改革的不斷深化和推進.其中課標Ⅰ卷理科第16與20題是三角與概率背景下的最值問題,讓人眼前一亮,切入點多,可利用多種方法進行求解,本文探討利用AM-GM不等式進行求解.
1.AM-GM不等式
在人教A版的必修五中介紹二元的AM-GM不等式,然后在選修4-5中進一步推廣到n元形式的AM-GM不等式,即:
對于n個正數ak,k∈*且k≤n,則有當且僅當a1=a2=…=an時,等號成立.記憶口訣為:“一正,二定,三等號”.
2.試題呈現
題1 (2018年課標卷Ⅰ理16)已知函數f(x)=2sinx+sin2x,則f(x)的最小值是.
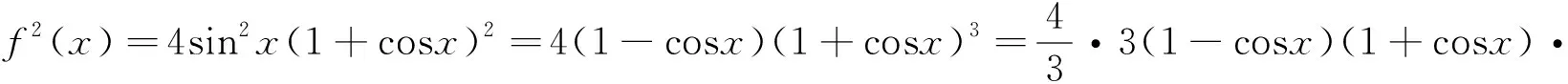
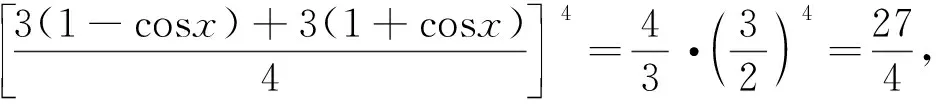
評析:試題以考生熟悉的三角函數入手,呈現方式也是考生所熟悉.考生比較容易考慮利用導數進行求解,但計算過程較復雜,需要考生具有扎實的基礎知識與運算能力.而根據AM-GM不等式的特點,把f(x)進行適當的變換,可快速解答,體現區分度,考查考生分析問題和解決問題的基本能力,體現中學數學素質教育的本質,促進數學素養的提高.
題2 (2018年課標卷Ⅰ理20)某工廠的某種產品成箱包裝,每箱200件.每一箱產品在交付用戶之前要對產品作檢查.如檢驗出不合格品,則更換為合格品.檢驗時,先從這箱產品中任取20件作檢驗,再根據檢驗結果決定是否對余下的所有產品作檢驗.設每件產品為不合格品的概率都為p(0 (Ⅰ)記20件產品恰有2件不合格品的概率為f(p),求f(p)的最大值點p0; (Ⅱ)現對一箱產品檢驗了20件,結果恰有2件不合格品,以(Ⅰ)中確定的p0作為p的值.已知每件產品的檢驗費用為2元,若有不合格產品進入用戶手中,則工廠要對每件不合格品支付25元的賠償費用. (ⅰ)若不對該箱余下的產品作檢驗,這一箱的檢驗費用與賠償費用的和記為X,求EX; (ⅱ)以檢驗費用與賠償費用和的期望值為決策依據,是否對這箱余下的所有產品作檢驗? (ⅱ)若繼續對余下的產品進行檢驗,則檢驗費用為2×200=400 評析:本試題考查二項分布的基礎知識、基本思想和方法.第(Ⅰ)問根據二項分布的定義,容易得到f(p),考生可以利用導數求最值的方法進行求解,很好地考查考生的數據處理與分析、應用能力;此時若考慮從AM-GM不等式入手,可以減輕考生的計算負擔,提高作答的時效性與準確性,有助于考生在緊張的考試中正常發揮,并能提高考生邏輯推理與數學運算的數學素養. AM-GM不等式是高中階段重要的不等式之一,在日常的學習過程中,可引導學生從不等式的“形”方面入手,也就是“一正,二定,三等號”,然后根據已知條件進行應用,解決問題.能有效地提高學生學習數學的興趣,實現課程標準的教學目的,促進學生數學素養的提高.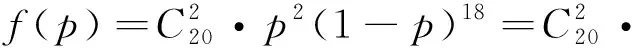
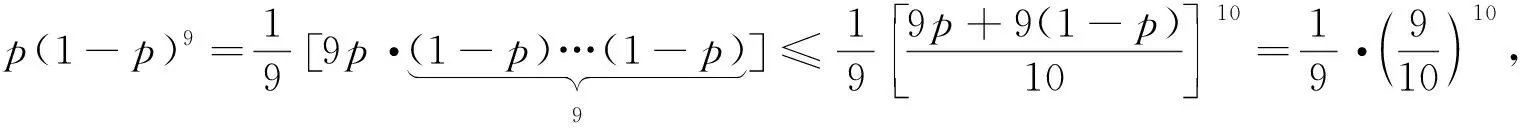
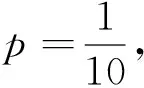
3.解題感悟

