一道平面幾何競賽題的解法展示與簡析
——命題者思路與學生解題思路的差異

江西省瑞金第一中學 (342500)

謝小平 楊祖華 許麗美

2018年全國高中數學聯賽江西省預賽已經落下帷幕，筆者有幸參加了今年贛州市的閱卷工作，發現這道平面幾何題很值得研究與思考.

題目如圖1,ΔABC的內心為I,D,E,F分別是邊BC,AC,AB的中點，證明：直線DI平分ΔDEF的周長.

讓我們先來看命題者提供的解題思路：

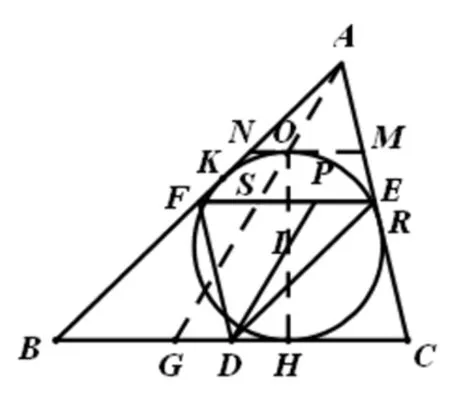
圖1

證明：作出ΔABC的內切圓⊙I分別切BC,AC,AB于H,R,K,連接HI并延長交⊙I于O,過O作BC的平行線分別交AC,AB于M,N,連接AO并延長交BC于G,設AG交EF于S.

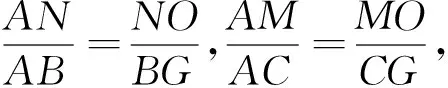
又D,E,F分別是邊BC,AC,AB的中點,∴AB=2DE,AC=2DF,BD=CD,BG=2FS,CG=2ES,∴2DE+2FS=2DF+2ES,∴DE+FS=DF+ES.

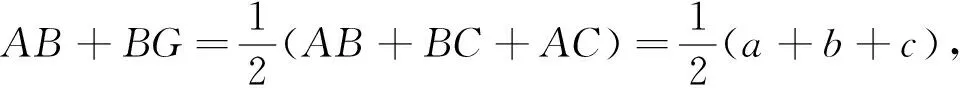
從命題者提供的參考答案容易看出，命題者的思路應該是來源于旁切圓的性質，即AO會平分ΔANM的周長，從而推導出一系列的等分周長的性質，進而得到此題的證明.但在實際的閱卷過程中，使用這種方法進行證明的學生是鳳毛麟角，大部分學生利用的是內心、角平分線的性質和相似三角形的關系進行證明,以下三種解法是在改卷過程中學生給出的解答.

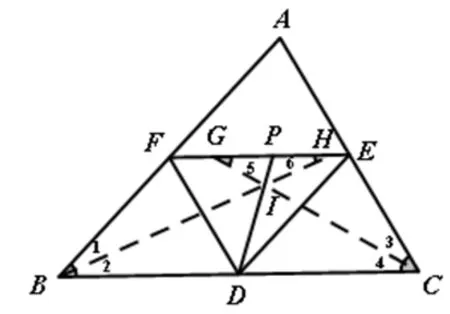
圖2

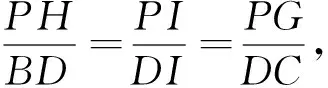
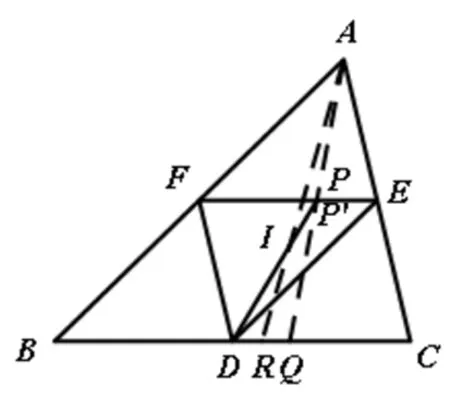
圖3

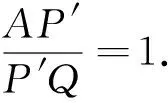
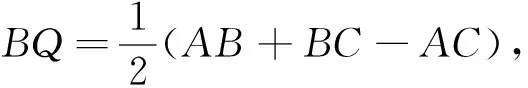
對ΔARQ及D,I,P′三點由梅涅芳斯定理,有

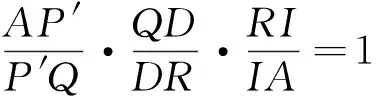
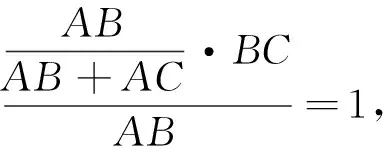
合.即P為ΔAEF內切圓在EF上的切點,∴PE+AF=PF+AE,又AF=DE,AE=DF,∴DE+EP=DF+FP,即直線DI平分ΔDEF的周長.

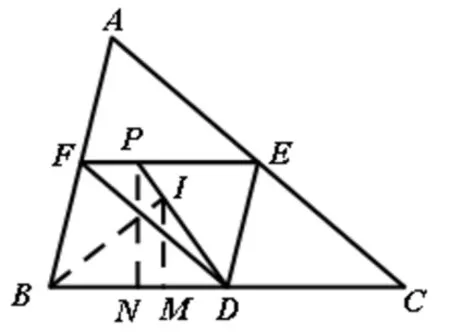
圖4

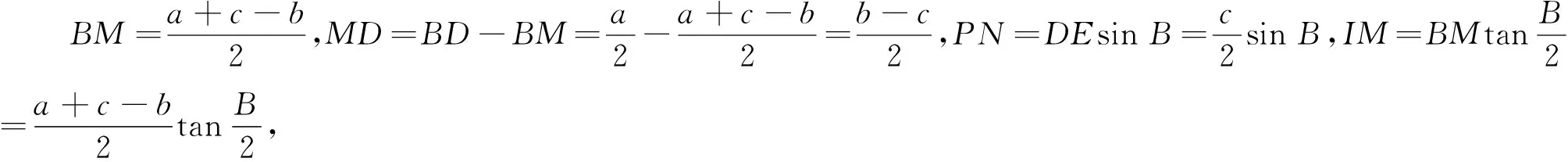
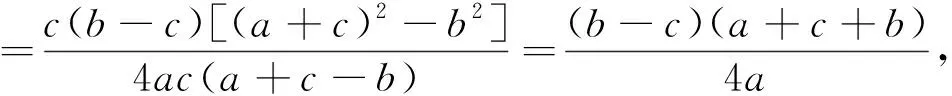
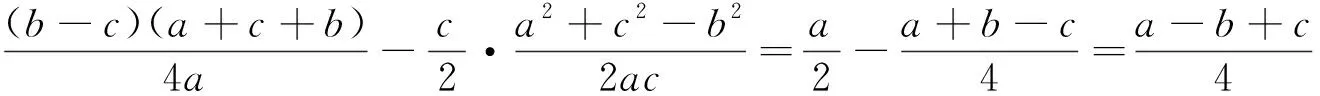
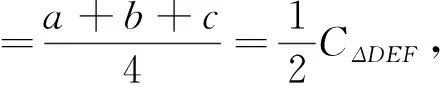
由于命題者在試題的圖形繪制中，隱去了三角形的內切圓，所以，幾乎沒有考生嚴格按照命題者給出的標答證題.但從以上考生的幾種證法可以看出，其證明過程都優于命題者，“教學相長”我們應該遵循這一教學規律.