一元立木材積表計算蓄積量誤差的探討
李愛華,孫秀君,周傳統,王恒均
(肥城市林業局,山東 肥城 271600)
利用一元立木材積表計算蓄積量誤差,一般是根據《數理統計原理》,計算出其標準差,以95%可靠性求算其誤差。但由于此方法計算過程比較復雜,因此,在實際工作中一般不求算調查蓄積量誤差。通過長期的工作實踐,我們總結了一種通過常用的《山東省一元立木材積表》結合徑階區劃求算蓄積量誤差的方法,簡稱:徑階區劃法。供參考。
1 計算方法原理
1.1 胸徑徑階區劃

表1 2cm徑階區劃
1.2 蓄積量計算
V=fgh
f-代表立木行數;g-代表立木胸高斷面積,單位:m2;h-代表樹高,單位:m。
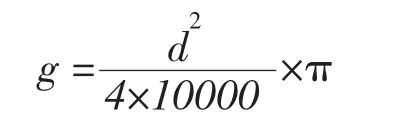
d-代表胸徑,單位:cm。
1.3 立木蓄積量(V)與胸徑(d2)正相關
由《測數學》可以得知:樹木的行數(f)一般相對穩定,當樹木達到一定的年齡后其高生長量也比較緩慢。由此,可以推論出立木蓄積量(V)與胸徑(d2)正相關。
即:V∝d2
由以上推論標準地的蓄積量(V總)與胸徑(∑d2i)正相關。
根據“2cm徑階區劃表1”可以得出:
V總下線∝(5.02+7.02+9.02+…)
V總上線∝(6.92+8.92+10.92+…)
V總∝(62+82+102+…)
1.4 蓄積量誤差的計算
由以上推論標準地的蓄積量誤差(E)可以用以下公式來求算,但需要注意的是在標準地調查時沒有的立木徑階值,不參與以下公式的計算,詳見下面的“2.2蓄積量誤差”章節的論述。
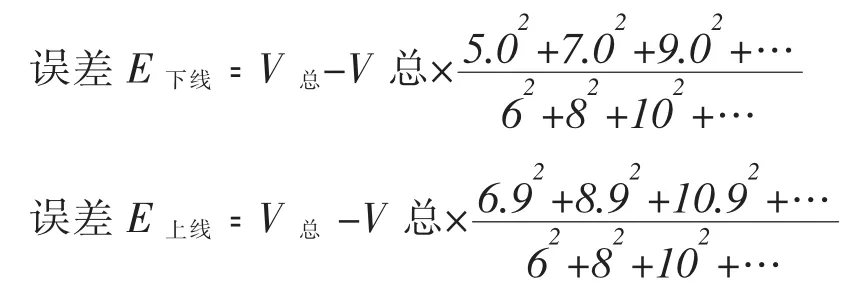
2 舉例論述
2.1 求算蓄積量
如某一楊樹標準地調查記錄計算結果見下表:
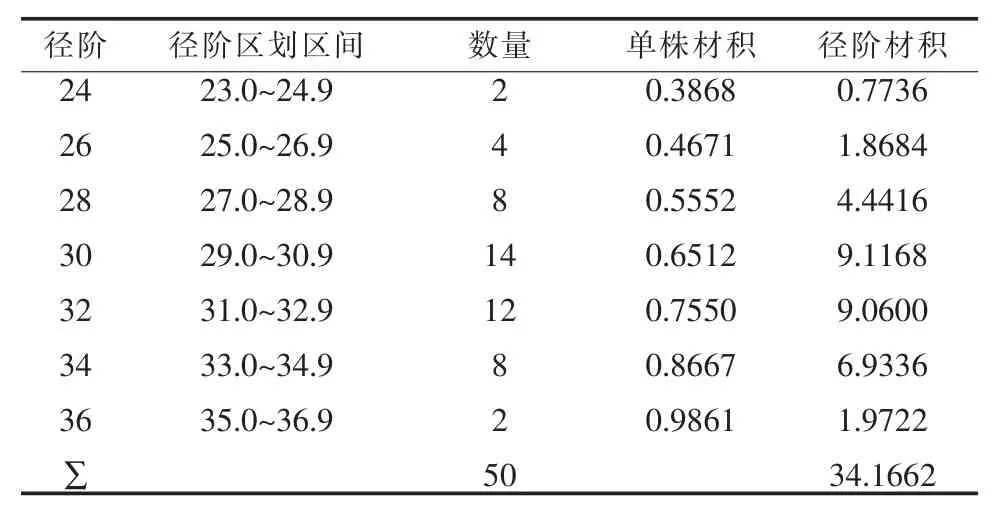
表2 標準地調查計算
2.2 蓄積量誤差
根據“1.4蓄積量誤差的計算”的論述,此楊樹標準地的蓄積量誤差可以進行如下計算。
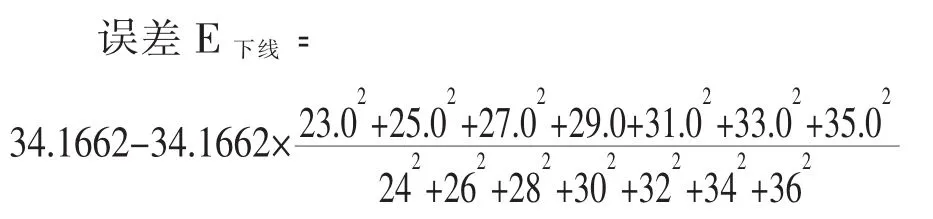

由以上計算結果得出:此標準地蓄積量區間值【31.9801(34.16622.1861)~36.1960(34.1662)】m3之間,或表示為:。
2.3 用《數理統計原理》求算蓄積量誤差
用《數理統計原理》,以95%的可靠性求算蓄積量誤差E=2.0022 m3
由此可得標準地蓄積量區間值【32.1640(34.1662.0022)~36.1684(34.1662.0022)】m3之間,或表示為:34.1662±2.0022 m3。
3 結論
由以上論述可以看出這種徑階區劃法,是利用《山東省一元立木材積表》結合徑階區劃計算出蓄積量誤差,與利用《數理統計原理》求算蓄積量誤差,兩者的誤差值相差不大。因此,此方法可以供林業工作者在今后工作中結合實際參考使用。

