數學建模促進大學數學教學改革
王志高 王永柱
【摘 要】數學建模活動作為高校科技實踐教學活動的一個重要組成部分,對基礎數學課程教學的改革有著越來越重要的作用。本文數學計算可視化、便利化;數學理論實用化的角度通過實際的案例展示了零點存在定理和均勻分布在數學建模中的精彩應用,讓枯燥的基礎數學知識點的講授變得有趣、有用,對學生數學學習的實現正面情緒激勵,體現了數學建模對基礎數學教學改革的促進作用。
【關鍵詞】數學建模;計算可視化;零點存在定理
中圖分類號: G712;O1-4文獻標識碼: A 文章編號: 2095-2457(2019)35-0271-002
DOI:10.19694/j.cnki.issn2095-2457.2019.35.131
1 數學模型相關的軟件計算對教學改革的影響
傳統的大學數學教學,知識內容更新緩慢,知識點之間的次序結構相對穩定,教學方法沿襲了課堂講授、課下安排大量作業題的方式。在課堂教學環節方面,隨著多媒體教學的興起,使得數學課堂教學朝著泛多媒體教學化的方向發展,但其本質還是把之前需要在黑板上一步一步寫下來的演算或者講解過程,提前寫在ppt上面,而實質內容上變化不大。
數學建模競賽的發展以及公共數學課課堂教學效果不佳的現實,促使大學數學老師在教學環節中更加重視一些數學建模案例和數學軟件的應用。使其跟大學數學課堂教學緊密結合。
大學數學教學過程中關于極限、函數性質是一個重點,同時也是學生從中學的初等數學學習向大學的高等數學學習轉變的一個關鍵難點。老師應用數學軟件通過畫圖、計算把一些原本不容易看到、不容易得到的結果展示給學生,這樣學生在學習過程中就會一下子豁然開朗,對概念的理解和方法的掌握就會更順利。
比如在微積分[1]課程《無窮大量和無窮小量》的講解過程中,有這樣的一個結論“無窮大量是無界的,但是無界的變量不一定是無窮大量”。老師要給學生講清楚這個事情,需要復雜的教學語言的組織。
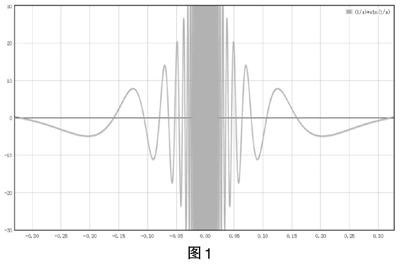
例1:函數y=■sin■在x→0時無界但不是無窮大量。
解:對于任意給定的M>0,
(1)xk=■,(k=0,1,2,3…),?圯y(x■)=2kπ+■
當k>M時,y(x0)>M,所以無界
(2)xk=■,(k=0,1,2,3…),?圯y(x■)=0
所以不是無窮大量。
上面數學證明是正確的,但是學生在聽課的時候,并不能很快接受。
圖1
此時如果用數學軟件畫出函數的圖像,學生就可以非常形象的感受到在x→0時函數的變化過程(可以通過調節兩個坐標軸的尺度,放大局部的圖像,更好的感受圖像的特點),就可以很好理解上述的數學證明。
再比如在線性代數課程的學習中,四階以上的行列式的計算[2]是學生比較發愁的一個事情。老師在相關內容的講授過程中,可以在傳統課本知識的講授基礎上,再給學生添加相關的學軟件的計算展示。
例2:計算行列式D=■,
傳統方法需要用的行列式的五條計算性質以及按行按列展開,需要花費較長的時間,并且很容易出錯。如果利用軟件去計算的,非常的簡單直接一行命令就可以。
以matlab軟件為例:
先輸入矩陣:D=[-2 2 -4 0;4 -1 3 5;3 1 -2 -3;2 0 5 1];
在執行計算:D=det(D)
可以在不到一秒鐘之內看到結果:D=-270
在老師增加了軟件計算的展示后,學生對數學計算題會有更多的思考,也掌握更靈活的處理方法。讓數學建模相關的數學計算軟件與傳統的數學課堂教學內容交叉,可以讓學生對所學的數學知識理解更深刻,掌握更靈活,課堂也更生動。
2 數學建模相關案例對基礎數學教學改革的影響
傳統的大學數學知識內容幾十年沒有什么變化,甚至大學數學在學生的心目中已經成為了枯燥、無用的形象。這樣在學生們學習數學知識的時候就會天然的帶著一種抵觸的情緒,使得本來就尷尬的大學數學教學變得處境更加艱難。一些優秀的數學建模案例的出現,恰好可以去改變這一局面。
函數連續性是微積分中的一個重要內容,在函數連續性相關的性質中,零點存在定理是一個很簡單的知識點,學生們往往覺得這么簡單定理,一看就會,沒什么意思,學了也沒什么用處。現在給出數學建模中一個案例,從中可以看到零點存在定理的應用。
例3: 把椅子往不平的地面上一放,通常只有三只腳著地,放不穩,然而能否稍挪動幾次,就可以四腳著地,放穩呢?
分析:解決問題之前,做些合理的假設,使得問題簡化。
(1)椅子四條腿一樣長,椅腳與地面接觸可視為一個點,四腳的連線呈正方形。
(2)地面高度是連續變化的,沿任何方向都不會出現間斷(沒有像臺階那樣的情況),即地面可視為數學上的連續曲面。
(3)對于椅腳的間距和椅腳的長度而言,地面是相對平坦的,使椅子在任何位置至少有三只腳同時著地[3]。
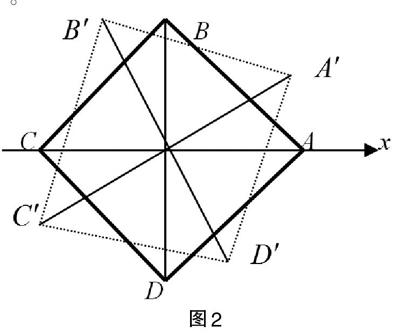
圖2
首先用變量表示椅子的位置,由于椅腳的連線呈正方形,以中心為對稱點,正方形繞中心的旋轉正好代表了椅子的位置的改變,于是可以用旋轉角度θ這一變量來表示椅子的位置。
其次要把椅腳著地用數學符號表示出來,如果用某個變量表示椅腳與地面的豎直距離,當這個距離為0時,表示椅腳著地了。椅子要挪動位置說明這個距離是位置變量的函數。
由于正方形的中心對稱性,只要設兩個距離函數就行了,記A、C兩腳與地面距離之和為f(θ),B、D兩腳與地面距離之和為g(θ),顯然f(θ)、g(θ)>0,由假設2知f(θ)、g(θ)都是連續函數,再由假設3知f(θ)、g(θ)至少有一個為0。當時θ=0,不妨設g(θ)=0,f(θ)>0,這樣改變椅子的位置使四只腳同時著地,就歸結為如下命題:
命題 已知f(θ)、g(θ)是θ的連續函數,對任意θ,f(θ)*g(θ)=0,且g(0)=0,f(0)>0則存在θ0,使f(θ0)=g(θ0)。
解:將椅子旋轉90°,對角線AC和BD互換,
由且g(0)=0,f(0)>0可知g■>0,f■=0。
令F(θ)=f(θ)-g(θ),則F(0)>0,F■<0,
由f(θ)、g(θ)的連續性知F(θ)也是連續函數,
由零點定理,必存在θ0使F(θ)=0,即f(θ0)=g(θ0),
由f(θ)*g(θ)=0,所以f(θ0)=g(θ0)=0
通過這樣一個數學模型的講解,同學們對數學知識的掌握會更為深刻,對數學本身的情感認知會發生好的轉變:數學還挺有意思,挺奇妙。尤其是在大學剛開始的時候給學生們講這樣一個案例,會極大的吸引學生,讓學生對大學數學的學習充滿興趣。同時對改進大學數學課堂教學有非常大的幫助。
【參考文獻】
[1]鄭紅芬.微積分[M].上海,上海交通大學出版社,2015.12.
[2]同濟大學數學系,線性代數[M].上海,同濟大學出版社,2015.
[3]姜啟源,謝金星,葉俊.數學模型[M].高等教育出版社,2015.

