三角函數中正余弦定理的實際應用方法探究

摘?要：正余弦定理是高中數學課程中必修內容之一，在高考中占有非常重要的地位，是解三角形的工具，與我們的日常實際生活也有著非常緊密的聯系，滬教版高中教材第6章《三角函數》中的制作彎管就是一個利用數學知識解決日常生活的一些問題，實現彎管的設計與制作，因此提出三角函數中正余弦定理的實際應用方法研究——以制作彎管為例，通過研究三角函數以及三角函數正余弦定理在彎管制作中的應用，并延伸到日常生活的實際應用，完成本文的研究，積累從具體到抽象的相關經驗，完成理論到實踐的研究。

關鍵詞：三角函數;正余弦定理;彎管制作

一、 引言

在高中數學課本中，已經開始注重理論知識與實踐相結合，為日常生活中的實際應用打下基礎，因此對于傳統的數學教學內容更加需要注重與現實素材相結合，實現利用數學知識進行實際生活的應用。提出了三角函數中正余弦定理的實際應用方法研究——以制作彎管為例這一課題，進行正余弦定理證明及證法，利用正余弦定理的逆命題，深入了解正余弦定理，了解三角函數在高考中的地位，高效完成高中課本的教學要求;提出彎管制作所利用的函數曲線并進行函數曲線驗證，實現正余弦定理在制作彎管中的應用，進一步延伸至正余弦的實際應用，完成本文的研究，幫助學生積累由具體到抽象，由理論到實踐的經驗，幫助他們更好地完成課本的學習，學會有邏輯的思考問題，并利用數學模型解決實際生活中的問題，提升創新意識與學習能力。

二、 正余弦定理的應用

（一） 測量距離問題

在數學課本中，三角函數中的正余弦定理用于解三角形，如知三邊解三角形，知兩邊一角解三角形等，對于不同的已知條件來判斷使用正余弦定理。對于正余弦定理這一數學模型也可在距離測量這一問題上進行研究，在實際生活中的測量距離首先需要選取合適的輔助測量點，構建出三角形，再將距離問題轉化為三角形的邊角關系。利用正余弦定理進行計算得到需要測量的距離，一般測量的距離都是兩點之間不可通也不可達的建筑或地理位置，例如河兩岸的距離，通常在河的一岸選取合適的輔助點，再選取對岸的兩點，使用儀器測出對岸兩點的距離以及這三個點圍成的三角形的三個角的角度，利用正弦定理解出三角形，計算出兩岸的距離。在實際的日常生活中，利用正余弦定理建立的數學模型在航海中應用的較為廣泛。

（二） 測量高度問題

對于利用正余弦定理測量高度這一問題，大多是將測量高度問題轉化為三角形的邊角問題，在實際日常生活中，通常是在測量建筑物的高度或者山峰的高度時使用的較為廣范，在高度測量時，需要選取輔助測量點，首先在與建筑物或者山峰的同一地平面選取輔助測量點，使用相關的儀器測量出輔助測量點到建筑物或者山峰的距離，以及輔助測量點與建筑物或山峰的最高點最低點所圍成的三角形的三個內角的角度，使用正弦定理解出三角形，計算出建筑物或山峰的高度。

（三） 零部件加工制作

在斜橢圓類零件制作中多應用到三角函數知識，無論是數控車削加工，還是人工不銹鋼彎管制作，都與三角函數解析、正余弦定理息息相關。在人們日常生活中不銹鋼彎管較為常見，下面就彎管制作中蘊含的正余弦定理，及制作過程加以研究。

三、 彎管制作中蘊含的正余弦定理

三角函數是一種刻畫客觀世界具體變化規律的數學模型，常用于解決日常的一些具體問題，例如：滬教版高中教材第6章《三角函數》就將制作彎管這一日常事物收入“探究與實踐”活動中。教材中以直角彎管為例，其由兩個截面角度為45°的斜截圓筒拼接而成的。拼接前需計算彎管斜截口展開后曲線，諸如此類的活動可以讓學生積累從具體到抽象的經驗，發展幾何直觀和空間想象能力，學會有邏輯地思考三角函數規律，積累不同的三角函數單調性、奇偶性、周期性、對稱性等數學模型，依托數據探索事物本質、關聯和規律的活動經驗，學會用數學模型解決實際問題，增強創新意識和科學精神。

學生參與彎管制作需要其自己動手來求截口展開曲線的函數解析式，可以通過在練習冊上描截口曲線來獲取彎管截面全部曲線。然后，引導學生在彎管截面曲線上建立坐標系，通過在彎管截面曲線上選取坐標點再測量的活動得到圖形，之后再采用TI圖形計算器進行函數擬合求出解析式等活動，深入學習三角函數有關課題，高效完成高中課本的教學要求。

（一） 正余弦定理

在三角函數中正余弦定理是用于解三角形的一種工具，通過利用正余弦定理解決了生活中遇到的一些難題，并且在數學發展的歷史進程中，受天文測量、航海測量以及地理測量等方面的實踐研究的影響，使得解三角形的理論也得到了發展，并解決了許多實際測量問題。通過正余弦定理證明及證法的研究，提出正余弦定理的逆命題，實現對正余弦定理的研究。

（二） 彎管制作中涉及的三角函數

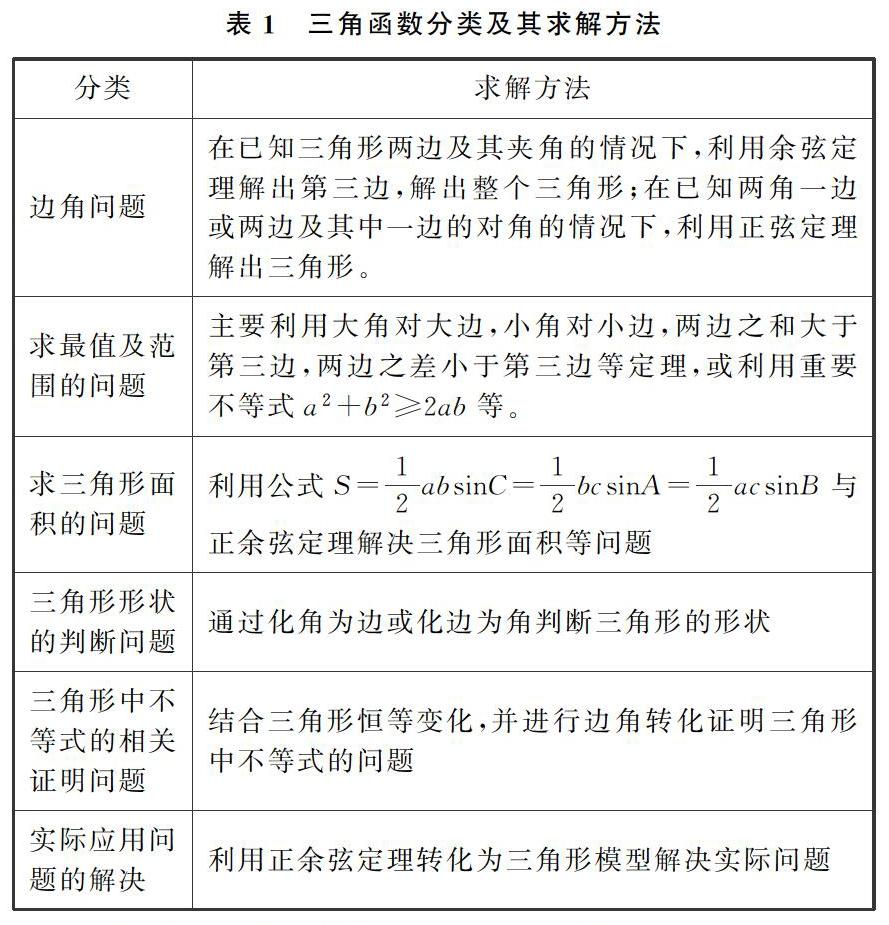
正余弦定理是三角函數解析中最常用的一種方式，用于解決已知三邊求解三角形，已知兩邊及夾角求解三角形或已知兩角一邊求解三角形等問題。現將三角函數中正余弦定理應用于彎管制作中，所涉及的三角函數知識點如下。如表1所示。

四、 正余弦定理在制作彎管中的應用

利用課本正余弦定理知識設計三角函數模型解決制作彎管遇到的一些問題，在彎管制作中由于彎管形狀難以使用澆筑或者粘接的方式進行制作設計，又彎管的形狀難以刻畫等的問題。利用數學模型進行相關的設計，通過研究發現三角函數中的正余弦定理可以較好地刻畫彎管的形狀，對于彎管的制作提供模型基礎，在彎管制作研究中，首先提出彎管制作可能利用的函數曲線，并進行相關的模型設計篩選，確定所用的函數曲線，進行函數曲線驗證，制作函數模型，實現正余弦定理在彎管制作中的應用，高效地完成彎管的設計工作并完成彎管的制作，可以大大的節省時間，提高制作效率。彎管如圖1所示：

（一） 提出彎管制作所利用的函數曲線

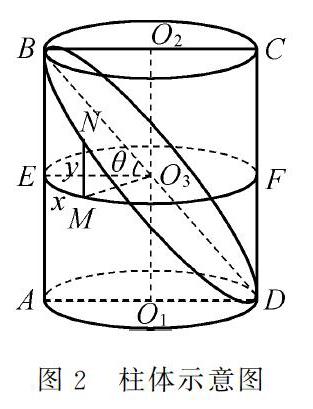
對于日常生活見到的一些彎管，很明顯是由兩個截面角度為45°的斜圓柱體拼接而成的，而對于拼接這一工藝來說是非常困難的，甚至是難以實現的，因此提出使用數學模型進行設計制作彎管，在此基礎下，將彎管進行裁剪，斜截口展開觀察其曲線特征，繪制彎管制作可能用的函數曲線，通過具體的實際操作研究發現，將彎管裁剪展開的曲線復合正弦函數、余弦函數曲線圖像的特征，如圖2所示。

對于不同傾斜角度的斜圓柱體的函數圖像有著不同的一些特征值，在我們平時的數學學習中我們了解到余弦函數圖像可以通過左右平移得到正弦函數圖像，同理，正弦函數圖像也可以通過一定的平移得到余弦函數圖像，通常將截口曲線的解析式表示為：

在正余弦函數圖像中A決定函數圖像高低，ω決定函數圖像的寬窄，不同的值有著不同的函數圖像，制作出不同型號的彎管。

在課本中引入彎管制作這一研究，利用三角函數中的正余弦定理，極大程度地將理論知識與實踐相結合，將實踐知識帶入課堂，提高了學生的積極性，一定程度上改善了數學教學的枯燥性、乏味性等，也將數學知識帶入生活，為同學們積累了具體到抽象的經驗，豐富想象力，鍛煉了邏輯能力，提升學生數學抽象的核心素養能力。

（二） 三角函數曲線驗證

對于解析式y=Asin（ωx+φ）+C進行驗證，進行實驗，首先是將截口缺陷圖像描繪在圖紙上，根據圖像合理的建立坐標系，選取一些特殊點或者是便于測量的點進行測量并標出坐標，最終使用計算機進行函數擬合解出解析式。在進行上述過程的幾組實驗使用不同的A，ω，φ，圓柱體半徑r，斜截面的傾斜角度θ以及C值，如表2所示。

通過多組圖像對比驗證①和②發現在半徑相同，其他不同的情況下，得到解析式中的ω較為接近，猜想解析式是ω與斜圓柱體的半徑相關，通過②和③的對比發現在θ值相同，其他值不同的情況下，得到的解析式A較為相近，猜想A通常受θ影響，即函數圖像的高低通過斜截面的傾斜角度進行變化。

通過上述研究發現函數曲線的解析式驗證這一環節，極大地調動了學生的積極性，通過自主探究進行解析式的驗證提高了學生的動手能力，增加了學習的自主性，在這一過程中較完整的建立起數學模型，帶動學生體驗到利用數形結合解決一些生活中的實際問題，提高了空間想象能力以及運用空間想象能力解決問題的能力。

（三） 三角函數與彎管問題的延伸

如圖1中彎管例圖可以看出，在彎管制作過程中，中間有數節兩端都為斜截面的管壁制作，俗稱“蝦米腰”。可以將其放大來思考，并將其伸展開，就能清晰直觀地看出其函數形式，如圖3所示。

將其伸展開后，就能發現上下兩端的MM及NN都是余弦線，若同時做多個此類兩端為斜截面的管壁，可在平面板上，連續畫出多條余弦線，不僅節約工時，更能夠節省原料。

此類問題可以讓學生先在紙上繪制圖樣、裁剪、折疊等方式，通過動手操作，驗證自己的設想，從而體會到三角函數正余弦定理在生活中的實際應用，做到活學活用，不只將數學定理知識局限于書本之中。

五、 結束語

三角函數中正余弦定理是我們高中必修課程之一，通過對三角函數中正余弦定理的研究學習熟悉了數學模型的建立，豐富了學生的想象力，本文通過正余弦定理的證明及證法研究，提出正弦定理的逆命題，完成正余弦定理的研究，使得學生熟悉了解正余弦定理，可以更好地應用，了解高中課本的教學要求，充分的實現理論知識與實踐的結合，實現對三角函數的初步研究;提出彎管制作所利用的函數曲線，對函數曲線進行驗證，實現正余弦定理在彎管制作中研究應用。

參考文獻：

[1]焦占紅.淺析“正、余弦定理”在解三角形中的應用[J].高中數理化，2017（18）：10.

[2]鐘理.正、余弦定理在解三角形中的應用[J].中學生數理化：高二高三版，2017（18）：18.

[3]管理.解斜三角形的實際應用案例分析[J].好家長，2017（58）：201.

[4]鄒松林.三角形最值題的常見類型[J].高中生，2017（36）：32-33.

[5]侯凱元.正余弦定理在生活中的運用[J].智富時代，2017（4）：412.

[6]洪武定.自創工具，開墾數學實驗課之地——一節正余弦定理的實踐活動課及反思[J].黑龍江教育（中學），2017（5）：16-17.

[7]丁志超.正弦、余弦定理的變換應用[J].高中數理化，2017（10）：9-10.

[8]趙艷平.正弦定理和余弦定理應用策略[J].高中數理化，2017（z1）：6-7.

[9]莊炯林.基于幾何畫板輔助生成的概念教學——以任意角三角函數為例[J].福建中學數學，2016（9）：40-42.

[10]阮珣.一次兼顧“理論與實用”的微課制作——以高中數學“任意角的三角函數定義”為例[J].福建中學數學，2016（9）：34-37.

作者簡介：

馬曉紅，江蘇省蘇州市，江蘇省蘇州市田家炳實驗高級中學。