從中考試題談初高中函數教學的銜接
葉 欣
(北京工業大學附屬中學 100022)
北京新課程改革方案逐步開始實施,其中變化之一是更加強調連貫性,要求義務教育九年一貫整體設置,關注小初銜接、初高銜接.義務教育階段所學數學知識相對具體,高中階段所學數學知識相對抽象,作為高中數學教師,了解學生義務教育階段所學內容、學習方式、能力水平,才能更好地幫助高一新生從初中過渡到高中學習階段.了解學生的學習狀況和基礎的途徑之一是中考數學試題.本文僅對中考函數類試題加以評析.
一、考查學生研究函數的基本經驗

例1 (2017年北京市中考第26題)如圖,P是弧AB所對弦AB上一動點,過點P作PM⊥AB交弧AB于點M,連接MB,過點P作PN⊥MB于點N.已知AB=6cm,設A,P兩點間的距離為xcm,P,N兩點間的距離為ycm.(當點P與點B重合時,y的值為0)
小東根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小東的探究過程,請補充完整:
(1)通過取點、畫圖、測量,得到了x與y的幾組值,如下表:

x/cm0123456y/cm02.02.32.10.90
說明:補全表格時相關數值保留一位小數
(2)建立平面直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;
(3)結合畫出的函數圖象,解決問題:當△PAN為等腰三角形時,AP的長度約為____cm.
本題以函數學習的全過程為背景,考查研究函數的內容與方法,通過取點、畫圖、測量、列表、描點和畫函數圖象探究變量之間的關系,這正是初中學生在課堂中學習函數的基本過程,利用建立的函數模型解決問題,則是感性認識到理性認識的升華.
二、考查學生對基本初等函數的理解
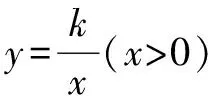
例3 (2018年北京市中考第26題)在平面直角坐標系xOy中,直線y=4x+4與x軸、y軸分別交于點A,B,拋物線y=ax2+bx-3a經過點A,將點B向右平移5個單位長度,得到點C.(1)求點C的坐標;(2)求拋物線的對稱軸;(3)若拋物線與線段BC恰有一個公共點,結合函數圖象,求a的取值范圍.
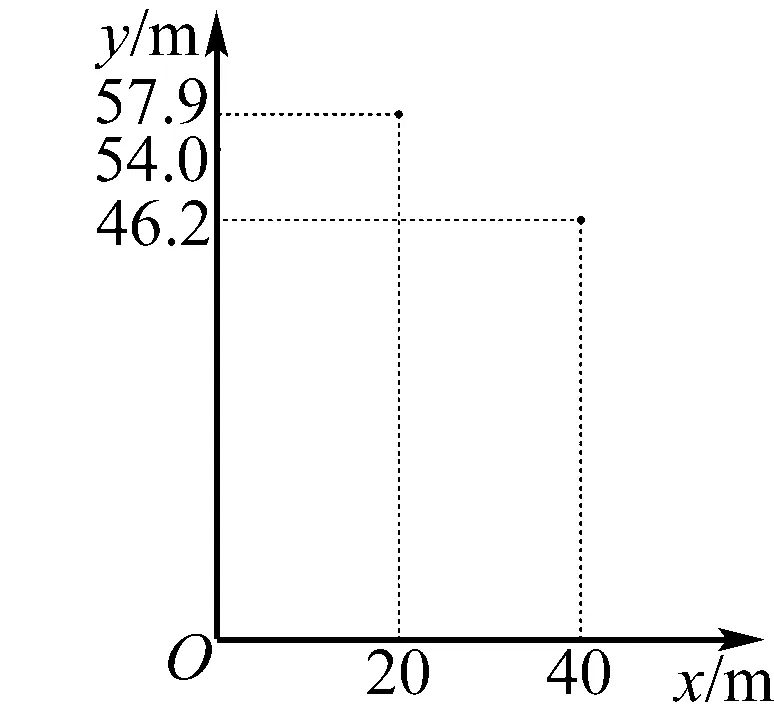
例4 (2018年北京市中考第7題)跳臺滑雪是冬季奧運會比賽項目之一.運動員起跳后的飛行路線可以看作是拋物線的一部分,運動員起跳后的豎直高度y(單位:m)與水平距離x(單位:m)近似滿足函數關系y=ax2+bx+c(a≠0).下圖記錄了某運動員起跳后的x與y的三組數據,根據上述函數模型和數據,可推斷出該運動員起跳后飛行到最高點時,水平距離為( ).
A.10m B.15m C.20m D.22.5m
這三個題目考查了學生對于一次函數、二次函數的理解.其中解決例2和例3中的問題需要從運動變化的角度思考問題,考查學生運用數形結合思想、分類與整合思想解決問題的能力.例4是運用二次函數相關知識解決實際問題的題目,該問題的解決是利用二次函數圖象的對稱性再結合題中所給數據,從數與形的角度直接分析推斷出二次函數的對稱軸,考查了學生靈活運用所學知識解決問題的能力.
三、對函數教學中初高中銜接的思考
函數概念在初中階段是以變量說定義的,體現了函數中變量之間的依賴關系,初中學生易于理解.高中階段則是用集合與對應的語言刻畫函數概念,抓住了函數的本質屬性,但其抽象性也給高一新生理解函數概念造成困難.在教學中應充分利用學生熟悉的實例和已經學習的函數幫助學生理解函數概念、抽象的函數符號以及函數性質,利用熟悉的情境降低學習新知的難度.高中對于指數函數、對數函數、冪函數、三角函數的學習幾乎延續了初中研究函數的經驗,因此對這些函數的學習完全可以由學生獨立完成.當然在教學中也要注意初高中的差異,即如何處理函數圖象與函數性質的關系,如果一味遵循由形到數、由特殊到一般,即由具體的函數圖象歸納該函數性質,對學生數學思維的培養是非常不利的.因此在教學中,既要關注初高中的關聯,創設情境讓學生在原有認知的基礎上學習新知,又要關注初高中知識、能力要求的差異,讓學生的思維能力和思維品質得到應有的提升.

