教師也要擇時“系統升級”

肖麗梅

摘 要：眾所周知，電腦軟件版本過低時就要及時更新升級，才能贏得市場。教師的教學方法也需要不斷更新，擇時“升級系統”，與時俱進，課堂教學才會永遠充滿生機和活力;課堂教學要不斷改進，從原始版躍到升級版，探索適合學生的教學方式，才能提高課堂效率。

關鍵詞：教學方法;原始版;升級版

中圖分類號：G623.5 文獻標識碼：A 收稿日期：2019-08-16 文章編號：1674-120X（2019）31-0065-01

案例一：植樹問題

原始版：用公式法解決問題。分兩種情況，第一種是在非封閉圖形中，①兩端都植時：棵數=段數+1;②兩端都不植時：棵數=段數-1;③只植一端時，棵數=段數。第二種情況是在封閉圖形中，棵數=段數。

升級原因：公式法使簡單問題復雜化。原來筆者總認為用公式法解決植樹問題嚴謹、周密、可靠，有一天解答了這道題：修一條長120千米的公路，如果每20千米由一個路隊負責，一共需要多少個路隊才能修完？學生列式為：120÷20-1或120÷20+1。于是，筆者靜下心來反思：學生錯誤的主要原因是生搬硬套公式。

升級版：畫圖分析法。只需重點引導學生畫圖分析 “只植一端”這一種情況，其余幾種情況不用再畫圖就能快捷地找到答案。例如，在一條長120米的小路一旁植樹，每隔12米植一棵，只在路的一端植，另一端不植，一共需要多少棵樹？筆者嘗試引導學生先畫圖分析。

不植? ?第1棵 第2棵? 第3棵? 第4棵? ?……? ? ? 第10棵

實踐證明，畫圖法幫助學生直觀形象、輕松自然地解決了問題。畫圖在學生以后的數學學習中會經常用到，可以說是一個終身受益的通用法寶。

案例二：雞兔同籠問題

在一個裝有雞和兔的籠子里，數頭有12個，數腳有32只，則雞和兔分別有多少只？

原始版：用假設法解決問題。假設法解決雞兔同籠問題的公式為：其中一種動物的只數=腳的總數量的相差量÷單只動物腳的數量的相差量。教師需反復強調：假設全是甲動物，則先計算出來的一定是乙動物的數量。

升級原因：筆者原來認為用假設法是解決雞兔同籠的最佳方法，簡潔、穩妥。但在下面一次練習課中，學生的表現讓筆者開始反省。

（1）有2元和5元紙幣共12張，合計39元，則兩種面值的紙幣各有多少張？

（2）在一個裝有雞和兔的籠子里，雞比兔多4只，腿38條，則雞、兔各有多少只？

學生面對像第1題這種無明顯雞、兔類動物的簡單變式題和像第2題這類稍復雜的變式題時，無從下手，難于動筆。顯而易見，導致學生束手無策的主要原因是教師的教法太呆板，這樣只能培養出會解答簡單問題的機器，只要把題稍微變式，他們就會像丈二和尚——摸不著頭腦。

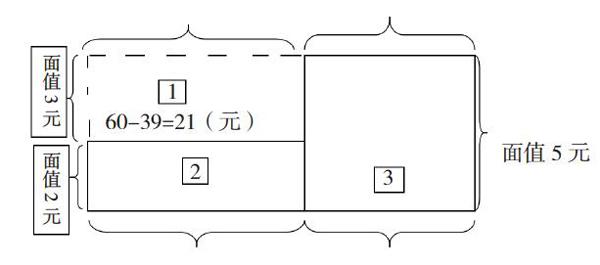
升級版：建立數學模型解決問題。凡是表達兩個數量相乘的積都可以建模為用長方形面積圖來表示，像上面第1題這種無明顯雞、兔類動物的雞兔同籠簡單變式題，筆者嘗試引導學生用建立數學模型的方法來解決問題。（參見下圖）整個大長方形的面積（即圖1+圖2+圖3的面積和）表示假設面值都是5元的紙幣時（也就是圖中大長方形的寬），總金額是12×5=60（元）。而圖1小長方形的面積表示這部分的金額是60-39=21（元），且它的寬很容易知道是5-2=3，那么它的長=面積÷寬，即21÷3=7（張），也就是面值為2元的紙幣實際張數是7張，則面值為5元的紙幣實際張數是12-7=5（張）。檢驗：實際總金額為5×5+2×7=39（元），符合題意。

2元紙幣：21÷3=7（張）? ? ?5元紙幣：12-7=5（張）

這樣下來，學生再解決這一類問題時，就可以做到 “茶壺里煮餃子——心中有數”了。

參考文獻：

[1]余文森，劉冬巖.有效教學的基本策略[M].福州：福建教育出版社，2013.

[2]楊慶余.小學數學課程與教學[M].北京：高等教育出版社，2004.