基于積分魯棒的電液伺服系統漸進控制

楊 洋

(南京航空航天大學,南京 210016)

0 引 言

針對電液控制系統中具有未知的動力學和有界擾動，許多方法相繼被提出[1]，其中自適應控制方法是一種有效的方法[2]。但是傳統自適應控制的響應可能由于控制器高增益而失穩，不利于保證系統的安全[3]。文獻[4]提出了一種新的魯棒自適應控制，這種控制可保證系統收斂于穩態，同時也可以調節系統瞬態響應。文獻[5]采用光滑摩擦模型來適應未知的非線性，同時針對近似誤差和其它有界擾動，利用誤差項符號的積分魯棒方法來補償。通過實驗研究驗證所提出的控制方法的有效性和改進的控制性能[6]。

針對上述問題，本文采用光滑摩擦模型來適應未知的摩擦非線性，利用誤差項符號的積分魯棒方法來補償近似誤差和有界擾動，最后進行了仿真對比，仿真結果表明，積分魯棒控制方法的輸出性能得到有效改進。

1 問題提出

本文所考慮運動位置伺服系統如圖1所示，其中Ps為油源壓力，Pr為理想氣體壓力。

圖1 電液位置伺服系統示意圖

慣性負載的運動方程：

(1)

式中：J和θm分別為系統轉動慣量和輸出轉角；PL為負載壓力；Dm為電動機排量；fm為運動系統的摩擦；f(t)為不確定干擾。PL的動態方程可以表示[6]:

(2)

式中：Vt為控制容積；βe為有效彈性模量；Ct為泄漏系數。QL可表示如下[5]：

(3)

式中：kt為流量系數；sign(u)定義如下:

(4)

(5)

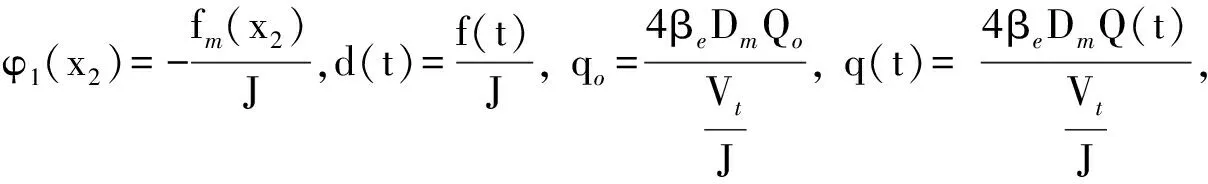
(6)

基于雙曲正切函數來近似適應摩擦模型可描述：

fm=θ1[tanh(c1x2)-tanh(c2x2)]+

θ2tanh(c3x2)+θ3x2

(7)

此靜態模型是關于速度的特性曲線，如圖2所示。取參數θ1=150，θ2=30，θ3=0，c1=200,c2=160,c3=200。

定義參數θ=[θ1,θ2,θ3]T，其相應的回歸器φ=[tanh(c1x2)-tanh(c2x2), tanh(c3x2),x2]T，則式(7)可參數線性化：

fm=φT(x2)θ

(8)

結合靜態摩擦模型式(7)，則式(5)可化:

(9)

式中：θo是對常值參數θ的辨識估計。

為便于控制器設計，做如下假設：

假設 1 此時的系統為不確定性有界，即：

(10)

式中：ξN2,ξN3為已知界。

2 誤差符號積分魯棒控制器設計

定義如下的誤差變量：

(11)

式中：k1,k2,k3均為正的反饋增益；e1為跟蹤誤差。

將式(9)代入式(11)可得:

(12)

將式(12)代入式(11)可得:

(13)

由式(13)，我們可設計魯棒控制器如下：

(14)

式中：kr>0為控制器增益；β>0為魯棒增益。

將式(14)代入式(13)可得：

(15)

對式(15)兩邊求微分可得：

(16)

3 穩定性證明

為了方便地分析魯棒控制器式(14)的潛在性能，引入如下的引理。

引理 1

定義：

L(t)=r[N-βsign(e3)]

(17)

(18)

若β滿足：

(19)

則輔助函數P(t)恒為正值。

證明：由式(17)，對其兩邊同時取積分，可得：

因此有：

由式(19)及式(21)知：

(22)

由引理1可知：

(23)

基于引理1，我們有如下的性能定理。

定理 1 對于非線性系統式(9)，若β滿足式(19)，且如下矩陣Λ：

(24)

為正定矩陣時，則t→∞時，e→0，其中e定義為e=[e1,e2,e3,r]T，并且可由誤差符號積分控制器魯棒項μ辨識系統的真實摩擦力，即：

(25)

證明：定義如下函數:

(26)

由式(12)及式(16)知：

又由式(24)定義的矩陣Λ正定知：

(28)

(29)

由定理1可知，只要魯棒增益β值取得足夠大，我們就可以獲得較好的摩擦補償效果。

4 仿真對比

文獻[5]中電液系統具體參數如表1所示。

表1 電液系統參數

系統跟蹤信號x1d(t)=0.2sin(πt)[1-exp(-0.01t3)]。為了便于對比，本文采用積分魯棒控制器(以下簡稱ARIPC)方法、誤差符號積分控制器(以下簡稱RISE)方法以及反饋線性化控制器(以下簡稱FLC)進行仿真對比。三種控制器的參數選取如下：

1)誤差符號積分魯棒控制器(ARIPC)：取控制器參數k1=250，k2=20，kr=2，β=2，自適應增益Г=diag{100, 50, 50, 50}。

2)誤差符號積分控制器(RISE)：即所設計的RISE控制器中不含模型補償部分。為保證對比公平性，其控制器參數與ARIPC控制器中對應的參數相同。

3) 反饋線性化控制器(FLC)：參照文獻[5]設計控制器如下：

式中：k1=5×104，k2=2×103，k3=200，χ=1。

圖3是系統在ARIPC控制輸入信號。ARIPC下系統對期望指令的跟蹤曲線、三種控制器作用下的跟蹤誤差分別如圖4，圖5所示。由圖5可知，ARIPC控制器的暫態和穩態跟蹤性能都要優于相對比的RISE控制器和FLC控制器，RISE控制器由于缺少模型補償，獲得較差的跟蹤性能，而FLC控制器既沒有自適應模型補償，也沒有非線性魯棒反饋則作用，獲得最差的跟蹤性能。

圖3 ARIPC控制輸入信號

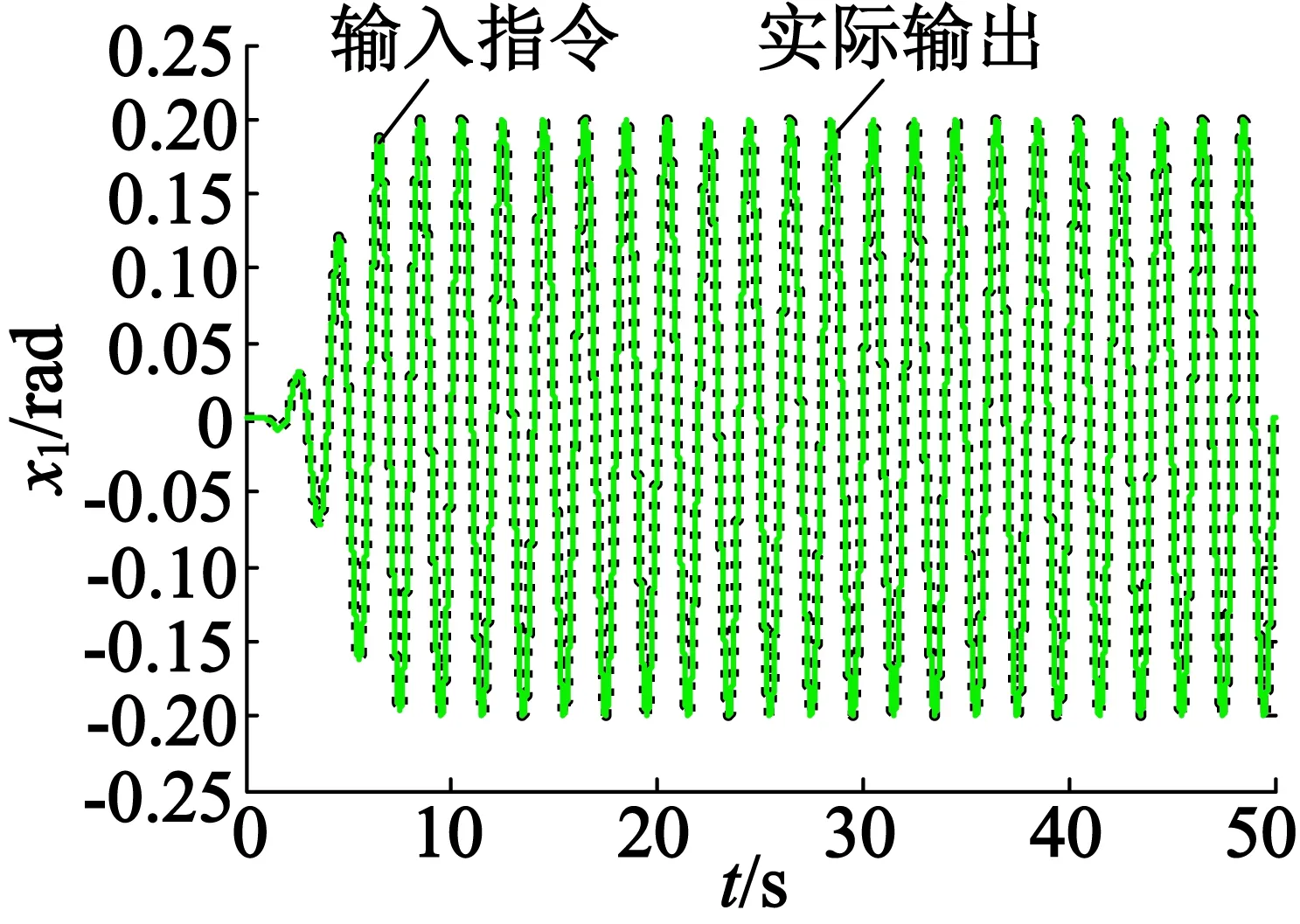
圖4 ARIPC下系統實際輸出曲線

圖5 系統跟蹤誤差曲線

5 結 語

本文針對電液位置伺服系統，采用光滑摩擦模型來適應未知的摩擦非線性，利用誤差項符號的積分魯棒方法來補償近似誤差和有界擾動。仿真結果表明，對比FLC和非線性RISE補償控制器，基于ARIPC的補償策略具有改進的輸出性能。