基于容量估算模型的交織區通行能力估計

馬曉旦，安 旭 （上海理工大學 管理學院，上海 200093）

0 引 言

高速公路上的擁堵在全球范圍內都被視為交通挑戰。在過去的研究中，高速公路的通行能力總是受到瓶頸的限制。在高峰時段，交織區可能會激活一個常發性的瓶頸。具體而言，交織區中合流區緊密地跟隨分流區并且兩股交通流交叉產生沖突[1]。交織或密集的換道行為甚至可能導致容量下降，這已經能夠在現場觀察到[2]。需要注意的一點是，通行能力是衡量交通運行并且緩解交通瓶頸的重要參數之一。更好地了解交織區對通行能力的影響可以增強高速公路的設計性和可操作性。

因此，長期以來一直有學者研究交織區以估計交織區通行能力，評估服務水平和分析安全影響。交織區設計和分析的相關方法第一次是在1950年的“美國通行能力手冊”（HCM）中提出。從那時起，許多研究都在努力改進HCM的相關方法。HCM 2000提出了通過將預測速度轉換為總密度來確定交織區的預期服務水平[4]。但是，此過程需要對路段分段以及需要對換道類型進行分類。為了解決這個問題，Roess和Ulerio開發了一個模型來替換具有車道變換行為和需求強度，這在實際應用中表現良好[5]。這種方法被加以開發應用，使用于像HCM 2010這樣的文檔中。對于安全方面的研究，有學者建立了單車道出匝的碰撞預測模型，以確定影響因素并發現左側道路傾斜可能導致更多的嚴重傷害和致命撞擊[6]。

在過去十年中，交織區的通行能力評估一直是運輸研究人員的主要關注點。通過經驗及理論手段已經開發了幾種直接的評估方法。對于經驗方法，HCM2000提供了詳細的步驟和通行能力確定的多頁表格[4]。后來，HCM2010中基于回歸模型的等式代替了HCM2000中的多頁表格。在最新的HCM模型中，交織區長度和交織區的車道數構成了衡量基本高速公路和交織區的通行能力之間的差異，該方法具有統計學意義[7]。此外，Kwon等人提出了基于卡爾曼濾波器[2]的通行能力估算方法，該方法根據來自上游主線和上匝道的收集數據估計交織區處的始發點至目的地的流量。然而，除了上述經驗模型中涉及的參數之外，復雜的駕駛員行為也可能影響交織區的容量。最后，研究還可以從理論的角度估計通行能力。

交織區通行能力評估的唯一理論模型是由Lertworawanich和Elefteriadou開發的[3,8]。該容量估計方法屬于線性優化問題，其中間隙接受理論用于約束交織車流。結果表明，復雜情況下交織區車輛的增加對交織區通行能力有顯著的影響。雖然該模型在測試中運行良好，但它不是為交通運行而設計的。因此，模型中基本交通運行設施難以直接測量其參數。其中，駕駛員行為參數可以是站點特定的。出于交通運營目的，進一步的研究使用車道變換模型取代了間隙接受理論，應用的車道變換模型由Laval等人提出，模擬車輛的縱向相互作用[9-10]。該模型將車道變化分為強制性和自由選擇，并確保微觀和宏觀測量之間的一致性。為了實現這一目標，它將車道特定的宏觀變量轉換為車道變化率，并將該速率離散化為時空點。評估結果符合合流和分流區域的觀察結果。該模型需要較少的輸入，并且在流量估計中更具適用性和通用性。

本文有四個目標：（1）開發一種使用車道變換模型和線性優化的交織區通行能力估算方法，該方法需要適用于實際的道路交通運行；（2）在兩種類型的交織區中評估建議的方法；（3）研究交織區通行能力與流量比例之間的敏感性和相關性；（4）估計高峰時段的實時最高通行流量。考慮到這些目標，本研究結合使用車道變換模型作為線性優化的約束。修改的交織區通行能力估算方法可能會對高速公路運營改進產生影響。

本文的其余分為幾個部分：提出的方法部分詳細介紹了該工作中的方法，包括線性優化問題和車道變換模型；飽和流率估算結果部分致力于分析飽和流率估算以及飽和流率敏感度；下一節是實時最大通行能力估算；最后，提出了結論性意見和未來工作的展望。

1 問題描述

高速公路交織區的通行能力是受許多因素影響的函數。在這些因素中，交織區包括四種O—D類型的運行車流，包括主路到主路、主路到匝道、匝道到主路以及匝道到匝道。在這四個流向中，車輛交織運行產生基本高速公路容量和編織能力之間的容量差異（如圖1所示）。基本的高速公路容量是指在沒有交織行為的情況下正常駕駛行為的容量。換句話說，交織比為零時實現了最高容量，即基本高速公路容量。一旦交織比大于零，容量就會降低到“通行能力”。基本的高速公路容量是Lertworawanich和Elefteriadou[3,8]中定義的等效高速公路段的正常容量。基本高速公路容量和交織區通行能力之間的差異是由交織行為（即，車道變換行為）引起的。簡而言之，交織車輛的車道變換行為會影響道路容量。

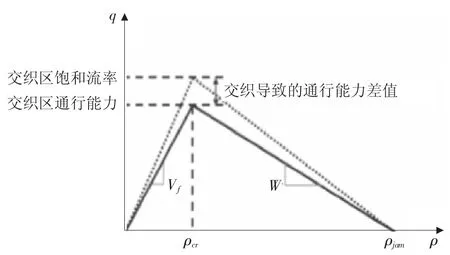
圖1 三角基本圖

以前的研究表明，最高流量和車道變換率發生在“關鍵區域”。在臨界區域內，車輛流量和車道變換率的函數可以定義為交織能力[11]。根據這一定義，本研究采用四步法估算交織織造能力。首先，需要基本幾何和交通信息來確定分段的類型特征。根據這些類型特征，交織段的最大長度（Lmax）參考HCM2010計算。如HCM2010中所定義的，體積比（VR）是交織路段處的交織流速與總流速的比率，并且NWL是可以通過一次或不需要車道變換可以完成交織行為的車道數。然后，僅將長度（Ls）小于Lmax的區段視為交織區段。其次，選擇具有車道變化集中度最高的區域作為交織區內的關鍵區域。同時，交通數據需要進一步減少以確定交織和非交織車流速度。接下來，對于交織行為中涉及的每個車道，其臨界密度應用于MH模型。從MH模型獲得的結果是交織車輛實際可以進行的最大車道變化次數。利用所有信息，通過應用上述容量的定義將容量估計問題建立為線性優化問題，同時通過若干交通運行約束來解決交織容量。

交織是在相同的大體方向上行進的兩個或更多個交通流的交叉。圖2顯示了交織區的兩種類型，以及用于描述交通流的符號。為了應用所提出的模型，研究的高速公路被分成若干段 （i=1,2,…,M）。如HCM2010中所定義的單側和雙側交織區在完成交織操作所需的強制車道變換的數量不同。

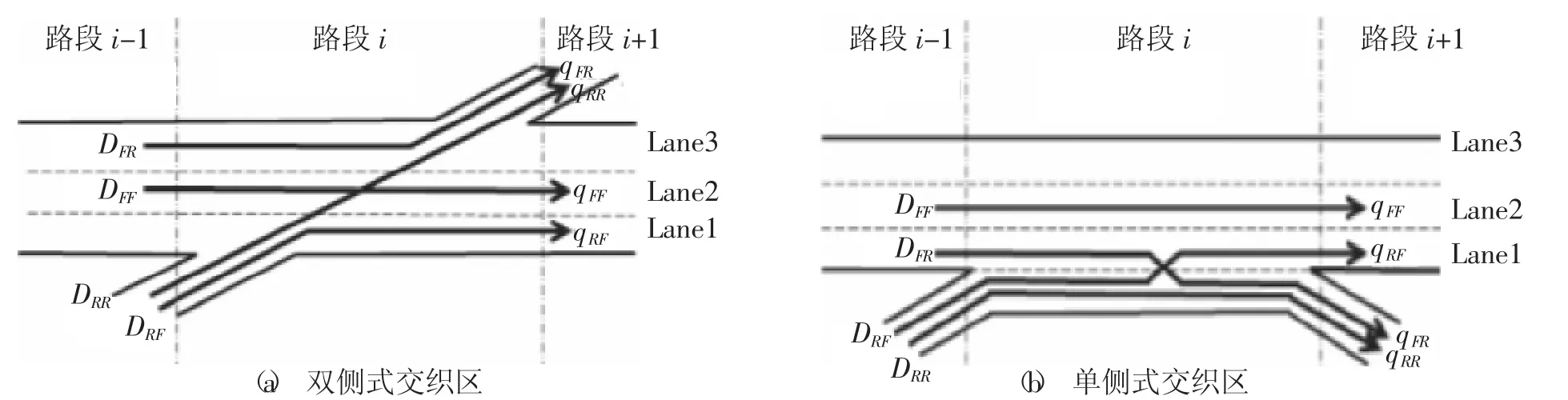
圖2 交織區結構圖

2 數學建模

在本文中，交織的容量被假定為四個流向在車道上的交通流量的總和。因此，交織能力可以在數學上表示為式（1），此外，還采用若干約束（式（2）至式（4））。式（2）和式（4）用于限制交通流量超過等效的基本高速公路和匝道容量。交織流動的約束 ［max（qRR）,max（qFR）和 max（qRF）］是交織通行的能力，其基于MH模型計算。先前的研究表明，交織能力高度依賴于交織流的比例[3,7,11-13]。每個流向的交織流量必須保持其需求的比率。因此，定義了式（3）中的W1和W2。在制定了所有約束條件后，可以通過使用線性優化技術估算交織路段的容量。

其中：cBF——交織區主路通行能力；cBR——交織區匝道通行能力；NF——交織區主路車道數量；NONR——交織區入匝車道數量；NOFR——交織區出匝車道數量；qFF——主路駛入至主路駛出車流量；qFR——主路駛入至下匝道駛出車流量；qRF——上匝道駛入至主路駛出車流量；qRR——上匝道駛入至下匝道駛出車流量。

3 案例模擬與分析

為了進行評估所提出的容量估算方法，本文研究了來自城市高速公路的兩個交織段。根據HCM2010中的定義，交織段的長度小于規定最大長度1.782km則為交織路段。案例中交織車輛必須穿過三個車道。僅上匝道到下匝道的交通流被認為是交織流，不考慮主路因為它不需要改變車道位置。這些區域附近安裝了車輛檢測站（VDS）和交通攝像機，VDS放置在主線、上匝道和下匝道上。裝置每20秒收集一次數據，包括速度和占用率，并將這些數據發送到中央計算機系統進行存檔。本研究中用作輸入的現場數據來自兩個獨立的來源：用于換道運動的錄制視頻，以及20秒為單位的VDS數據。按照實際案例將交織路段分為三個區域，從交通視頻中以1分鐘的間隔手動提取并收集相關的車道變換行為，每個區域的車道變化次數是從下午4:00到6:00收集的。

圖3顯示了來自VDS的體積密度圖，車道1和車道2具有相似的交通容量，但車道2在隊列消散期間經歷了更大的下降。同時，車道2和車道3具有相似的V—D模式，而車道2顯著小于最左邊的泳道。第2道和第3道的容量下降是由排隊引起的，可以解釋為：交織車輛在進入車道后將從1號車道轉向2號車道、2號車道轉向3號車道。此外，車輛在最右邊的車道上行駛最慢，在最左邊車道上行駛最快。

圖3 交織區車流密度圖

表1總結了來自VDS的交通數據，車輛計數的20秒間隔數據被匯總為5分鐘的間隔；表2列出了模型輸入參數，包括流速、流量比和基本容量值；表3總結了HCM2010方法和容量估算方法。與HCM2010相比，容量估算方法有類似的結果。從這些結果可以得出結論，所提出的方法適用于容量估計并提供合理的估計。

分析發現，當流量比（ ）W大于0.85時，交織能力保持在基本容量。然而，一旦W小于0.85，交織能力隨著W的比率增加而降低，這種敏感性表明交織車輛的增加降低了交織能力。此外，交織能力很少受到小交織流的影響，但隨著交織流量的增加，交織能力迅速下降。這些結果與Lertworawanich和Elefteriadou[8]的結果一致。

4 結束語

復雜的交織區瓶頸通常是由車道變換行為引起的過度交織操作引發的，由于交織行為對交織能力有重大影響，本文提出了一種將線性優化與車道變換模型相結合的容量估算方法。該方法在真正的交織區中進行評估以及驗證。這項研究有三個主要的發現：（1）大多數車道變化發生在合流區附近；（2）將HCM2010結果與實地觀察相比，容量估算方法有更好效果；（3）當交織流量比小時，交織車輛的影響很小，當交織比例較大時，交織行為顯著降低交織能力。通過部署適當的控制率，可以調整交織瓶頸中的實際駛入流量，此操作可以緩解瓶頸區域的擁堵。

表1 交通數據表

表2 模型輸入參數

表3 效果對比表