全國名校雙曲線拔高卷（A卷）

■江蘇省泰州市興化第一中學(xué) 劉偉華

一、選擇題

2.中心在原點,對稱軸為坐標(biāo)軸的雙曲線C的兩條漸近線與圓(x-2)2+y2=1都相切,則雙曲線C的離心率是( )。

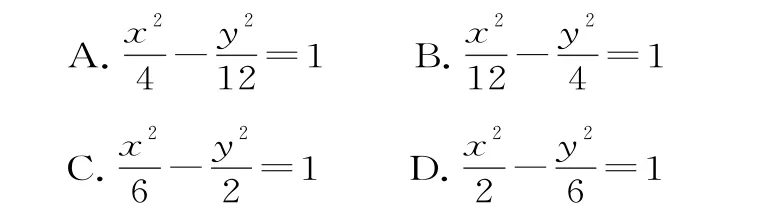
5.設(shè)雙曲線,離心率e=2,右焦點為F(c,0)。若方程a x2-b x-c=0的兩個實數(shù)根分別為x1,x2,則點P(x1,x2)在圓x2+y2=8的( )。

A.外部 B.圓周上

6.設(shè)F1、F2是雙曲線C:＞0,b＞0)的左、右焦點,A為左頂點,點P為雙曲線C右支上一點,|F1F2|=10,P F2⊥O為坐標(biāo)原點,則

7.已知M(x0,y0)是雙曲線=1上的一點,F1、F2是雙曲線C的兩個焦點,若則y0的取值范圍是( )。

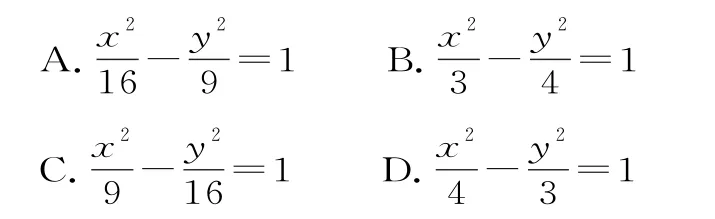
11.已知定點F1(-2,0),F2(2,0),N是圓O:x2+y2=1上任意一點,點F1關(guān)于點N的對稱點為M,線段F1M的中垂線與直線F2M相交于點P,則點P的軌跡是( )。

A.直線 B.圓

C.橢圓 D.雙曲線

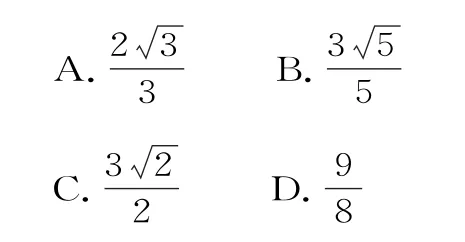
14.設(shè)F1、F2是雙曲線＞0,b＞0)的左、右焦點,P是雙曲線C右支上一點,若|P F1|+|P F2|=6a,且△P F1F2的最小內(nèi)角為30°,則雙曲線C的離心率為( )。

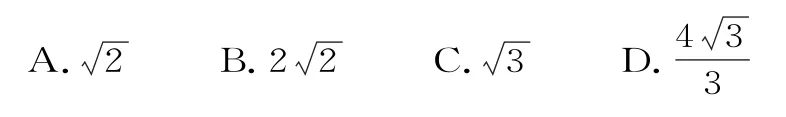
16.已知F1、F2是雙曲線＞0,b＞0)的左、右焦點,P是雙曲線上一點,且P F1⊥P F2,若△P F1F2的內(nèi)切圓半徑為,則該雙曲線的離心率為( )。

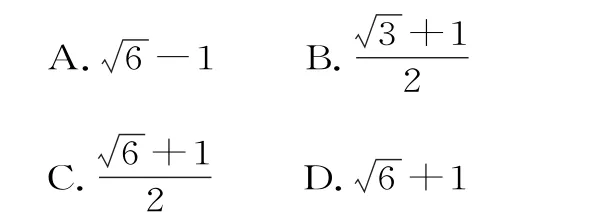
17.已知F1、F2分別是雙曲線的左、右焦點,若雙曲線E上存在一點P使得,則雙曲線E的離心率的取值范圍是( )。

A.(1,2) B.(2,+∞)

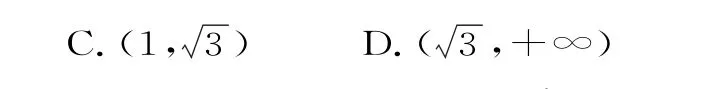
22.如 圖1,F1、F2是雙曲線0,b＞0)的左、右焦點,過F1的直線l與雙曲線C的左、右兩支分別交于點A、B。若△A B F2為等邊三角形,則雙曲線的離心率為( )。

圖1

23.已知F1、F2分別為雙曲線1(a＞0,b＞0)的左、右焦點,P為雙曲線右支上的任意一點,若的最小值為8a,則雙曲線的離心率e的取值范圍是( )。

24.設(shè)雙曲線的左、右焦點分別為F1、F2,過F1作傾斜角為的直線與y軸和雙曲線的右支分別交于點A、B,若,則該雙曲線的離心率為( )。

25.若雙曲線C:x2-y2=1的右頂點為A,過A的直線l與雙曲線C的兩條漸近線交于P,Q兩點,且,則直線l的斜率為( )。

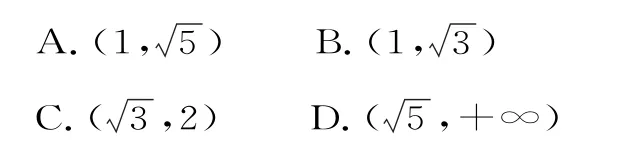
28.已知F1、F2是雙曲線＞0,b＞0)的左、右焦點,過點F2與雙曲線的一條漸近線平行的直線交雙曲線的另一條漸近線于點M,若點M在以線段F1F2為直徑的圓外,則雙曲線離心率的取值范圍是( )。

29.已知雙曲線0),A1、A2是實軸頂點,F是右焦點,B(0,b)是虛軸端點,若在線段B F上(不含端點)存在不同的兩點Pi(i=1,2),使得△PiA1A2(i=1,2)構(gòu)成以A1A2為斜邊的直角三角形,則雙曲線離心率e的取值范圍是( )。

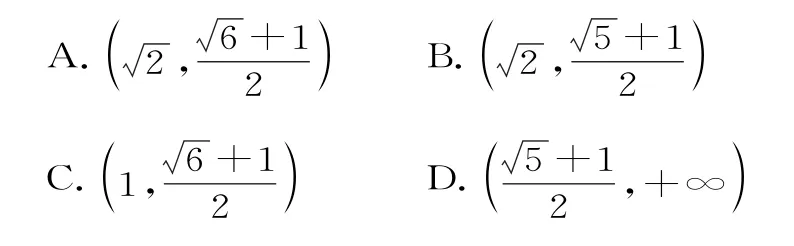
的一條漸近線上位于第一象限內(nèi)的點,∠A O F=∠O A F,△A O F的面積為33,則雙曲線C的方程為( )。

31.已知橢圓和雙曲線有共同焦點F1、F2,P是它們的一個交點,∠F1P F2=60°,記橢圓和雙曲線的離心率分別的最小值是()。

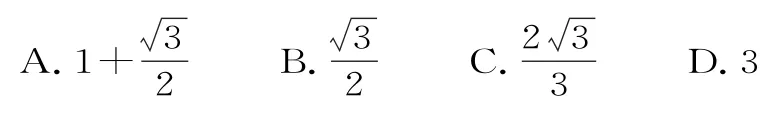
′1,且F′1是以F2為圓心,以半焦距c為半徑的圓上的一點,則雙曲線C的離心率為( )。

35.已知F1,F2是橢圓與雙曲線的公共焦點,P是它們的一個公共點,且|P F2|＞|P F1|,橢圓的離心率為e1,雙曲線的離心率的最小值為( )。

A.3 B.4

C.5 D.與點P的位置有關(guān)

A.8 B.4 C.2 D.1

38.已知F1,F2是橢圓和雙曲線的公共焦點,且A,B兩點為橢圓C1,雙曲線C2在第二、四象限的公共點,若四邊形A F1B F2為矩形,則雙曲線C2的離心率為( )。

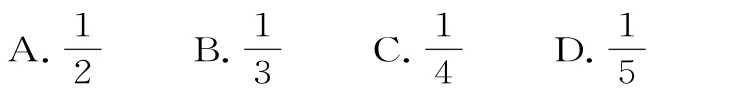
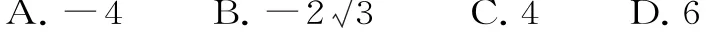
二、填空題

42.設(shè)F1、F2分別為雙曲線=1的左、右焦點,P為雙曲線C在第一象限上的一點,若,則△P F12F內(nèi)切圓的面積為____。

43.過點M(-6,3)且和雙曲線x2-2y2=2有相同的漸近線的雙曲線方程為

44.如圖2所示,橢圓中心在坐標(biāo)原點,F為左焦點,A,B分別為橢圓的右頂點和上頂點,當(dāng)F B⊥A B時,其離心率為此類橢圓被稱為“黃金橢圓”,類比“黃金橢圓”,可推算出“黃金雙曲線”的離心率e等于____。

圖2

51.在平面直角坐標(biāo)系中,O為坐標(biāo)原點,過雙曲線C:x2-y2=a2(a＞0)的右頂點P作射線l與雙曲線C的兩條漸近線分別交于第一象限的點M和第二象限的點N,且的面積為S=3,則a=____。

56.若F1、F2分別是雙曲線(a＞0,b＞0)的左、右焦點,O為坐標(biāo)原點,點P在雙曲線的左支上,點M在直線上,且 滿 足),則該雙曲線的離心率為

59.如圖3,等腰梯形A B C D中,A B∥C D且A B=2,A D=1,D C=2x(x∈(0,1))。以A,B為焦點,且過點D的雙曲線的離心率為e1;以C,D為焦點,且過點A的橢圓的離心率為e2,則e1+e2的取值范圍為

圖3

三、解答題

60.求滿足下列條件的雙曲線的標(biāo)準(zhǔn)方程:

61.已知雙曲線的中心在原點,焦點F1、F2在坐標(biāo)軸上,離心率,且過點(4,

(1)求雙曲線的方程。

(2)若點M(3,m)在雙曲線上,求證:MF1⊥MF2。

(1)求證:點P到雙曲線C的兩條漸近線的距離的乘積是一個常數(shù);

(2)設(shè)點A的坐標(biāo)為(3,0),求|P A|的最小值。

63.已知雙曲線的中心在原點,對稱軸為坐標(biāo)軸,一條漸近線方程為,右焦點為F(5,0),雙曲線的實軸為A1A2,P為雙曲線上一點(不同于A1,A2),直線A1P,A2P分別與直線交于M,N兩點。

(1)求雙曲線的標(biāo)準(zhǔn)方程;

64.已知動圓P過點F2(2,0)并且與圓F1:(x+2)2+y2=4相外切,動圓圓心P的軌跡為C。

(1)求曲線C的軌跡方程;

(2)過點F2(2,0)的直線l1與軌跡C交于A、B兩點,設(shè)直線,點D(-1,0),直線A D交l于M,求證:直線BM經(jīng)過定點(1,0)。

65.已知中心在原點的雙曲線C的右焦點為(2,0),實軸長

(1)求雙曲線的方程;

(1)求曲線E的方程;

(2)設(shè)曲線E′表示曲線E的y軸左邊部分,若直線y=k x-1與曲線E′相交于A,B兩點,求k的取值范圍;