在線協作式網絡社交媒體博弈論分析
——以問答式社區為例

楊圣琴，彭宇楠，馮月陽

（北京信息科技大學經濟管理學院，北京 100192）

一、引言

技術的進步改變了知識生產的模式，從工業革命前的政府主導到第二次工業革命后的企業主導再到互聯網時代的大眾生產，社會大眾利用互聯網在線協作式網絡社交媒體分享各自經驗知識、回答他人提問，這種人人參與、知識共享的模式有著極大的成功[1]，維基等百科社區、知乎等提問式社區、微博等話題類社區都成為在線協作知識平臺的典型代表。這類協作知識平臺對社會教育有極大價值，大眾可以在這些社區群組尋找問題答案，遠程教育也在利用網絡社交媒體促進學習群組之間的協作。

協作是這些社區群組成功的關鍵，大量網絡社交媒體用戶通過提問—回答的協作方式產生大量知識內容，但在這些應用中，隨著時間的推移，因為用戶可能對討論的主題失去興趣或者用戶提出的問題沒有得到滿意的答復，他們就會減少甚至停止在這些網絡社交媒體應用的活動[2]。如果某些用戶試圖利用群組協作性希望其他用戶回答他們的問題而忽略他人的提問以謀求利益最大化，還可能產生自私行為，這種自私行為也被稱為“搭便車”。“搭便車”的行為無疑會挫傷其他回答問題的用戶的積極性，導致社交網站的知識內容越來越少，用戶量也隨之消失[3]。

為了分析這種自私型用戶的行為及其對網絡社交媒體應用中群組的影響，本文基于針鋒相對策略，將所有用戶之間的互動視為非合作的重復博弈（一次博弈回合即一個用戶提出問題，群組內其他用戶回答/忽略該問題的全過程）。本文采用經濟學的觀點，假設用戶是理性的，其目的是實現其自身利益最大化，當其他用戶與他們協作時，他們的收益會增加，創建一個模型模擬眾多用戶在網絡社交媒體應用中組成群組以便進行協作，模擬用戶行為調整后的結果，利用針鋒相對策略和慷慨針鋒相對策略研究“搭便車”行為對網絡社交媒體應用群體及其生命力的影響。

二、模型及假設

在協作網絡社交媒體應用中，用戶合作可以采取多種形式，如回答他人的要求、參與討論或簡單地評論他人的知識貢獻，用戶也可以選擇不合作（即不對網絡社交媒體應用的問答做出貢獻）。運用博弈論，這種合作與不合作的情況可以模擬為非零非合作博弈。非零是因為用戶為群組做出貢獻的收益是協作和分享知識，這種利益不能轉移，而是由兩個人分享，不合作是因為每個人都是獨立地做出自己的決定。

表1 囚徒困境收益矩陣

模型參考著名的囚徒困境博弈論模型，兩個犯共謀罪的人被關進監獄，相互之間不能溝通，兩人都不揭發對方（合作）則因證據不足各獲刑一年；若相互揭發（相互背叛）則因證據充足各獲刑兩年；若一人揭發而另一人沉默，揭發者立功立即釋放，沉默者獲刑五年。在每一次博弈回合中，囚徒1和囚徒2都有兩種策略供選擇：合作或者背叛，他們都合作時每人得分為R；都選擇背叛則每人得分為P；一方背叛一方合作，則背叛者得分為T，合作者得分為S；通常，T＞B＞P＞S，2R＞T+S。

在囚徒困境博弈中，主要策略是在不管對方如何決定的基礎上做出對自己最有利的行動。在囚徒困境中，當兩個罪犯不知道對方的決定時，對罪犯的最佳策略是揭發他人，從而避免T＞R＞P＞S這種最糟糕的情況。但是，在博弈無限次的情況下，如果2R＞T+S，那么最好的策略就變成為兩人都沉默。

這種經典的囚徒困境不能模擬一個協作小組，因為在網絡社交媒體中，兩個用戶之間的決定不是同時做出的，而是分兩個階段做出的，因此以本文的參考文獻[4]提出的異步博弈囚徒困境構建本文模型。

（一）模型假設

假設在網絡社交媒體應用中有一組用戶，數量為N，每個用戶都是群組成員，分為合作型用戶（數量為Nc）、自私型用戶（數量為Ni），用戶發布的帖子僅限于群組內部，每個用戶都能夠發布問題請求他人回答、回答他人的問題、忽略他人的提問。將獲得他人回答的收益記為Ag=9，未獲得他人回答的損失記為Ad=-8，回答問題的成本記為Ac=-2，忽略問題的成本記為Ai=0，則R=Ac+Ag，P=Ai+Ad，T=Ai+Ag，S=Ac+Ad。Ac小于0是因為回答問題需要時間和精力來編寫答案，Ai=0是因為從一次博弈回合來看，忽略他人提問并不能帶來任何損失且有更高的收益，Ai-Ac小于Ag-Ad代表回答問題的成本低于獲得回答的獎勵，因此，從長期來看，理性的用戶最好彼此合作。每個用戶有兩種策略：合作（回答他人提問）、背叛（忽略他人提問），每個用戶回答問題的有用性概率記為Pu，0＜Pu＜1/10以模擬用戶的知識和時間精力方面的差異。

還假定：網絡社交媒體可以跟蹤每個用戶的所有提問和回答行為并形成記錄；網絡社交媒體更新每個用戶與其他用戶的合作狀態記錄；群組壽命是無限的，即博弈的次數是無限的。

用MATLAB模擬博弈過程，博弈運行1000回合，在每個回合中，將隨機選擇群組中的1/15個用戶提出問題，其余用戶可以選擇回答或忽略這些問題，模型假定不管什么原因忽略問題就是背叛。

（二）自私行為的影響

為了研究自私型用戶的影響，本文設置兩組群組：一組擁有150名用戶且都為合作型；第二組擁有150名用戶，其中70%是合作型，30%是自私型。兩組用戶的平均收益如圖1，其中橫軸代表博弈回合數，縱軸代表用戶的平均收益。可以看出無自私型用戶存在的群組用戶的平均收益在每次博弈中都高于自私型用戶存在的對照組，隨著博弈次數的增加，兩組平均收益的差距在擴大。

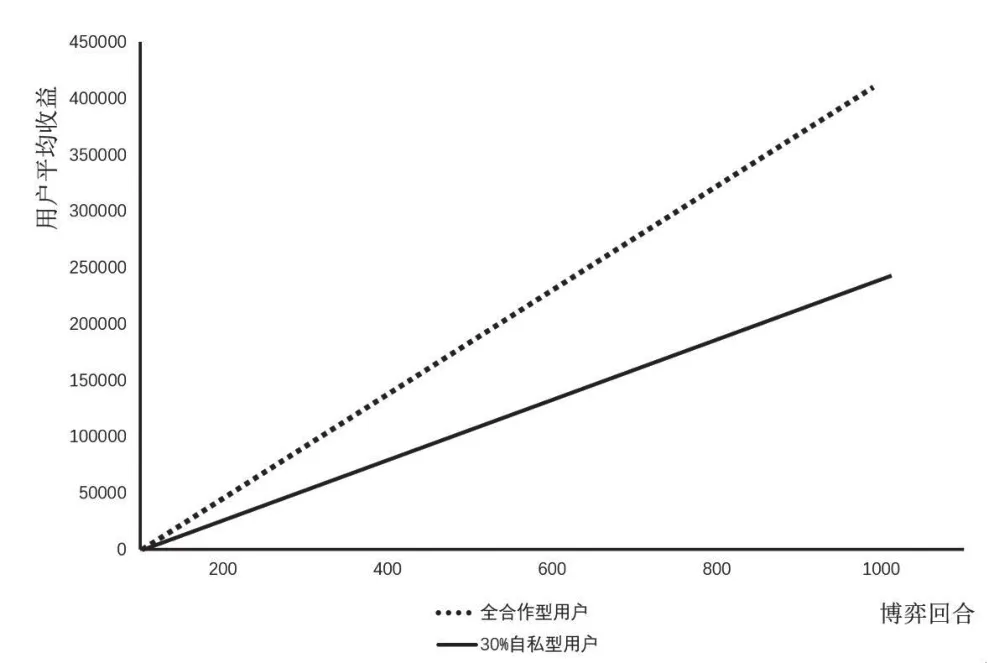
圖1 兩組用戶的平均收益對比

三、針鋒相對戰略

通過使用MATLAB模擬分析自私用戶對合作用戶收益的影響，以及增加自私用戶百分比對群組的影響以及影響程度。每個用戶的行為策略又分為兩種：一種是針鋒相對策略，另一種是慷慨針鋒相對策略。針鋒相對策略是：從不忽略一個不好的博弈回合，當雙方合作的博弈次數超過背叛的博弈次數時，合作型用戶才會選擇和另一個用戶進行合作。慷慨針鋒相對策略是：從不忽略一個好的博弈回合，但有時要忽略一個不好的回合，如果發現另一個用戶在某一時期內至少合作一次，即使出現過背叛行為，在下一回合中也會以一定概率選擇合作。

（一）針鋒相對策略

在針鋒相對策略中，用戶回顧其他用戶在上一回合中的行動并由此采取行動。在博弈中，假設用戶可以查看其他用戶的n次行動，用戶j能夠回顧與另一用戶i在n次迭代中的行為記錄Bji。每個Bji(t)的值對應著用戶i做出的決定Dij(t)，即用戶i是否在t時刻與用戶j合作，根據Bji(1)至Bji(n)的行為記錄，用戶j將做出決定Dij(t)，即是否與用戶i進行合作。如果從Bji（1）到Bji（n）的值之和大于n/2，用戶i將被視為合作型用戶，用戶j將嘗試與用戶i合作；否則，合作就不會出現。模擬結果如圖2。

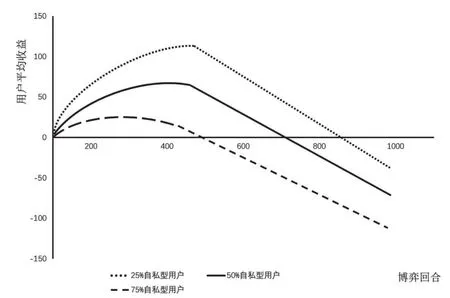
圖2 針鋒相對策略下不同數量的自私型用戶的合作型用戶平均收益對比

圖2顯示了在自私型用戶占群組用戶總數量的25%、50%、75%情況下，150個用戶都使用針鋒相對策略后合作型用戶的平均收益。可以看出，盡管自私型用戶的數量不同，但各群組合作型用戶的總回報陷入僵局并開始下降。原因是在這種策略下，即使是合作型用戶，也會有1-average(Pu)概率的用戶選擇不回答問題。結果，合作型用戶與另一個合作型用戶就會產生不合作的記錄，導致兩者都各自產生不合作記錄，從而無法再進行合作。由于用戶得不到任何答案的回報為-8，因此總回報持續下降。同時可以看到，群組中的自私用戶數量越多，回報進入僵局的速度就越快。這次模擬得出結論：即使是在合作型用戶之間，使用針鋒相對策略會導致協作減少。

（二）慷慨針鋒相對策略

慷慨針鋒相對策略能夠避免因協作減少而陷入僵局的情況。在慷慨針鋒相對策略中，合作型用戶j將無視其擁有的與用戶i從1時刻至n時刻的行為記錄Bji(1)至Bji(n)，在n次迭代中定期和用戶i進行合作。在過去的行為記錄中，一次的回答記錄就可以判定某一個用戶是合作型的用戶。模擬結果如圖3。

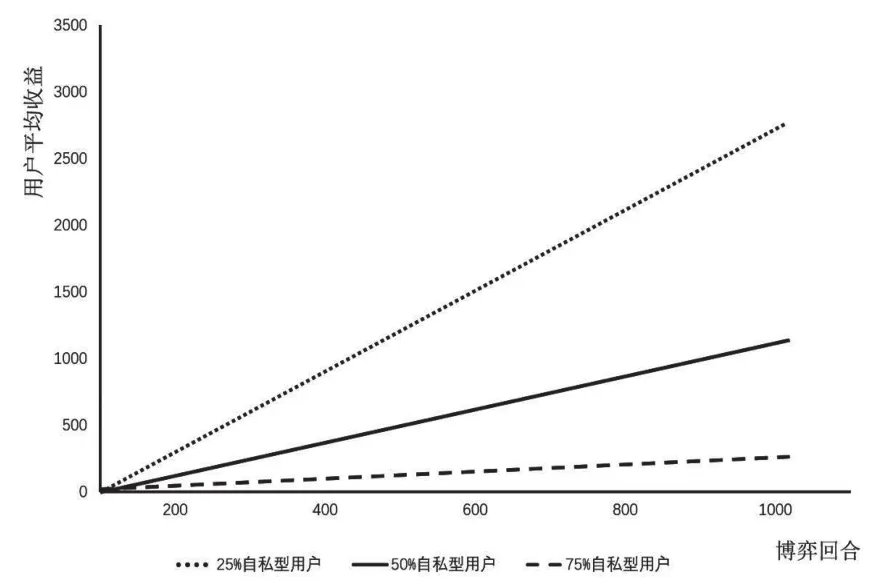
圖3 慷慨針鋒相對策略下不同數量的自私型用戶的合作型用戶平均收益對比

圖3顯示了在自私用戶占比25%、50%、75%的情況下，150個用戶都使用慷慨針鋒相對策略的合作型用戶平均收益，可以看到慷慨針鋒相對策略阻止了針鋒相對策略形成的僵局。

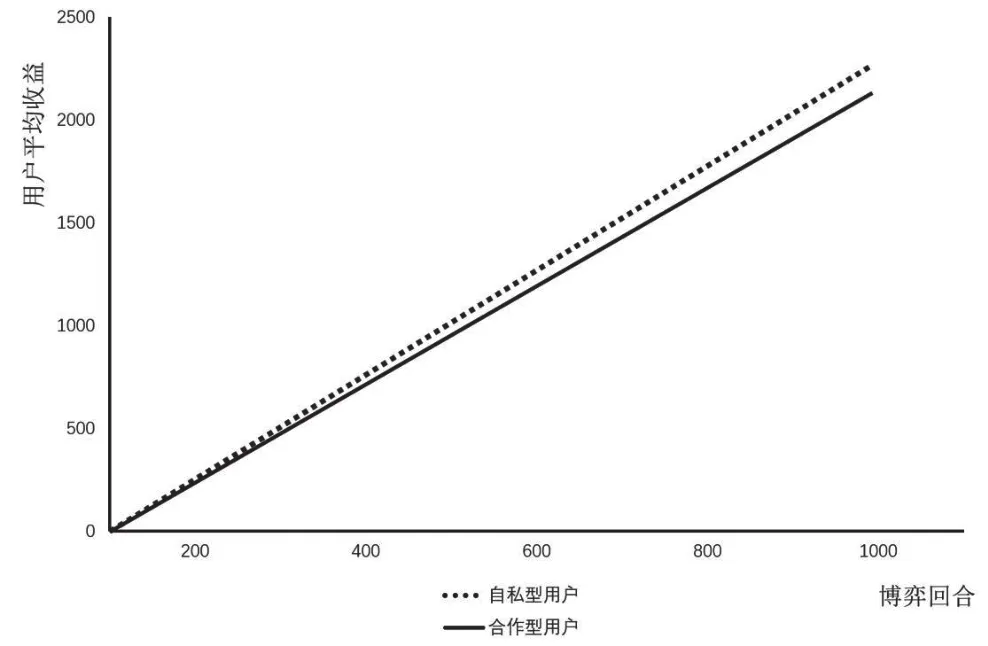
圖4 50%自私型用戶行動變化后合作型用戶與自私型用戶收益對比

在1000次博弈的某些回合中，如果自私型用戶與下一個博弈對象沒有合作記錄，其可能會改變他們的行為，合作一次以偽裝成合作的形象。這種行為的結果如圖4所示。結果表明，即使偶爾合作，如果自私型用戶合作的次數都沒有超過合作型用戶合作次數的1/5，自私用戶的利益就會略高于合作用戶，這是因為自私用戶保持著他們的最低貢獻。強迫自私用戶加強合作的一個方法是增加用戶被視為合作型用戶所需的合作數量或者增加可回顧的行動數量n。

慷慨型針鋒相對策略可增強整體協作，自私型用戶能夠很容易地利用這個策略，這也將導致用戶喪失合作動機，但對整個群組來說，慷慨針鋒相對策略優于針鋒相對策略。

四、結論

結果表明，慷慨針鋒相對策略比針鋒相對策略更能夠增強在線協作式網絡社交媒體群組中的協作，但這兩種策略都不能解決群組中的“搭便車”行為。網絡社交媒體可以采取一些措施來加強群組中的協作，如最大化合作型用戶的收益，最小化自私型用戶的收益，用激勵合作的方式取代消除的方式來對待自私型用戶。