論向量在解決高中數學問題中的應用
■江蘇省宿遷中學 蔣 健
高中數學試題復雜多變,應用向量的幾何、坐標運算以及相關性質,對數學試題進行轉化,可大大降低解題難度,使學生迅速找到解題突破口,提高解題正確性,幫助其樹立良好的解題自信,因此,授課中應做好數學試題匯總,向學生展示向量在解題中的應用,提高學生向量應用意識,使其牢固掌握、靈活應用這一重要的解題工具。
一、向量用于解答最值試題
求解最值是高中數學最為常見的一種題型,解題方法多種多樣,可應用均值不等式、函數、向量法求解,其中向量可化抽象為具體,不僅有助于理解題意,而且還能簡化解題步驟,及時解出正確結果。
授課中為使學生認識到向量法在解答最值問題中的妙用,掌握向量解題的技巧,應優選經典例題,為其詳細板書解題過程,給其解答類似習題,提供良好指引。
例1,已知a,b,c∈R,a+2b+3c=6,則a2+4b2+9c2的最小值為______。
很多學生看到該題目采用不等式知識求解,但多數無功而返,部分學生雖然得出正確結果,但花費時間較多,代價太大,在測試中是不可取的。授課中,可引導學生認真觀察已知條件以及要解決的問題,聯想所學的向量知識,應用向量方法解答。
解題中可設m=(1,1,1),n=(a,2b,3c),根據向量 性 質m · n≤|m| · |n|,可 得
該題從向量角度入手,巧妙運用向量性質進行轉化,經過簡單計算便得出正確結果,解法新穎,使學生眼前一亮,使其掌握解答最值問題的又一重要思路,很好地鍛煉其解題思維,獲得預期教學效果。
二、向量用于解答三角形試題
解三角形是高考常考題型,占有較高分值,通常應用正弦、余弦定理進行求解。但部分試題應用向量知識,可獲得事半功倍的良好效果,因此,授課中應注重講解三角形相關知識的向量表示,引導學生構建三角形與向量之間的關系。另外,創設相關問題情境,鼓勵學生運用向量法解答,并做好向量法解題的總結與反思,提高三角形試題解題效率。
例2,在△ABC中,角A、B、C對應的邊分別為a、b、c,若則△ABC 最小角的正弦值為:____。
觀察可知,因題干中給出有關向量的已知條件,因此,學生不難想到應用向量法解答。解答該題目的關鍵在于靈活轉化給出的等式關系,確定三角形的最小角,而后運用余弦定理進行求解,具體解題過程如下:

在解答該題目中,部分學生盲目求解,未搞清楚最小角便急于計算,結果走不少彎路。通過該題目的解答,可使學生深刻地認識到向量的工具性以及在解答三角形試題中的重要性,很好地提高其應用向量解答三角形試題的意識,為其順利、高效解題奠定良好基礎。
三、向量用于解答立體幾何試題
立體幾何涉及的知識較多,對學生的空間想象能力要求較高。解答立體幾何試題有常規方法和向量方法,其中向量方法只要找到相關點的空間坐標,借助空間向量知識求解即可,對空間想象能力不好的學生而言是一種重要解題方法。授課中為使學生牢固這一方法,應注重相關例題的講解,提高學生空間向量的應用方法與技巧,靈活用于解答各類立體幾何試題。
例3,如圖1,四棱錐P-ABCD 中,底面為矩形,PA⊥底面ABCD,PA=BC=1,AB=2,點M 在PC 上,試確定點M的位置,使得BP⊥面ADM。
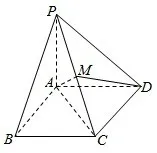
圖1
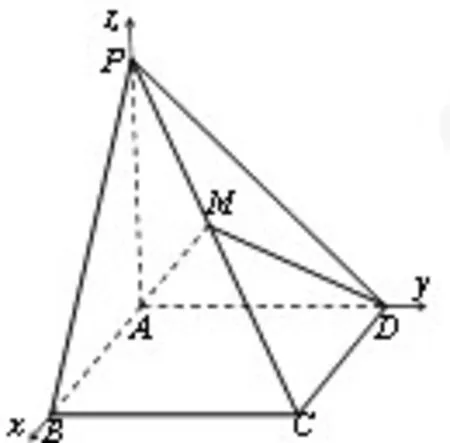
圖2
分析可知,該題目中存在三條邊垂直的情況,因此,可考慮采用向量法求解。以A點為原點,以AB、AD、AP 三條邊為x、y、z 軸,建立空間直角坐標系,如圖2所示。則P(0,0,1),A(0,0,0),B(2,0,0),C(2,1,0),D(0,1,0),設M(a,b,c),∵M 在PC 上,則令1),即,(a,b,c-1)=λ(2,1,-1),則M(2λ,λ,1-λ),要想滿足BP⊥面ADM,則,則,可知M在靠近點P,CP線段的五等分點上。
在立體幾何試題中確定點的坐標難度較大,采用常規做法多數學生不知如何下手,而使用向量,將其轉化為坐標的形式,問題便迎刃而解。
四、向量用于解答解析幾何試題
高中數學中解析幾何試題以計算煩瑣、難度大而著稱,是各類測試的重要失分題型,因此,授課中為提高解析幾何試題的正確性,除為學生講解常規解題方法,還應引導學生具備靈活應用所學的意識,即用好向量這一重要解題工具。以經典題型為例,與學生一起分析,采用向量知識尋找解題突破口,使學生認識到向量在解答解析幾何試題中的便捷性。
例4,如圖3,橢圓的中點在坐標原點,焦點在x軸上,A1、A2、B1、B2為橢圓的頂點,F2為右焦點,延長B1F2和A2B2交于點P,若∠B1PB2為鈍角,則該橢圓的離心率的取值范圍為:______。
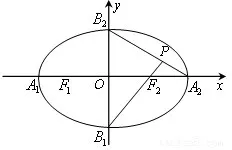
圖3
解答該題的關鍵在于怎樣正確運用“∠B1PB2為鈍角”這一條件。根據所學知識不難想到運用向量知識可表示出鈍角這一條件,即,借助對應的坐標關系便可求解。
由已知條件可知A2(a,0),B2(0,b),F2(c,0),B1
解答解析幾何試題時,能夠讀懂,正確利用已知條件是關鍵。通常將已知條件轉化為向量之間的關系,實現求解。正如本題,使用向量之間的關系表示鈍角,很快找到解題突破口。
五、結語
向量與高中數學其他知識點聯系緊密,在解題中應用廣泛,可顯著提高解題質量與效率,因此,授課中應做好高中數學試題總結,明確能應用向量解題的題型,尤其針對不同題型優選經典習題,講解向量在解題中的具體應用,鼓勵學生認真體會,反思解題過程,掌握向量解題的技巧,不斷提高解題水平與解題能力。

