思維盲點在哪兒?*
2019-03-08 02:11:22江蘇省海門市海門中學226100樊陳衛
中學數學研究(江西) 2019年2期
江蘇省海門市海門中學 (226100) 樊陳衛
很多數學問題在解題過程中存在一些容易被忽視的環節或要點,比如不等式兩邊同乘于一個參數或未知數時,會忽視這個參數或未知數是正是負還是零的討論;集合問題中往往忽視空集這一特殊情況;運用點斜式或斜截式直線方程時可能會忽略斜率不存在的情況;運用等比數列求和公式時有可能忘記了對公比是否為1的討論.對于諸如此類存在思維盲點的問題,解題時要時刻保持警惕.教師可以在教學中充分挖掘這些問題的價值,有意識引導學生在解題時不斷反思,捕捉解題思維過程中的盲點,培養思維的嚴密性和深刻性.筆者以一個分式函數問題為例加以剖析:
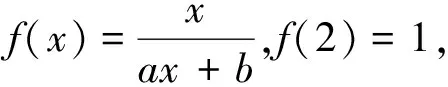
這道題看似不難解決,只要把問題進行簡單轉化和變形,根據方程f(x)=x有唯一解這一條件,容易求得a,b的值.可從學生解答的實際情況看事實并非如此.筆者有意把學生的普遍思路在課堂上呈現出來,師生探尋整個解題過程中的思維盲點.
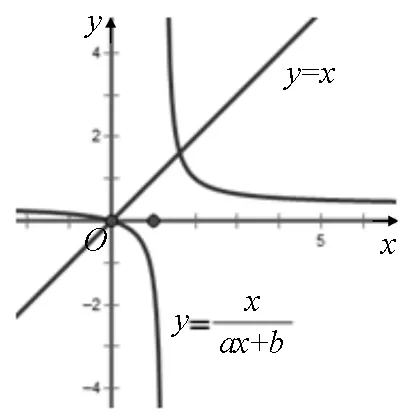
圖1
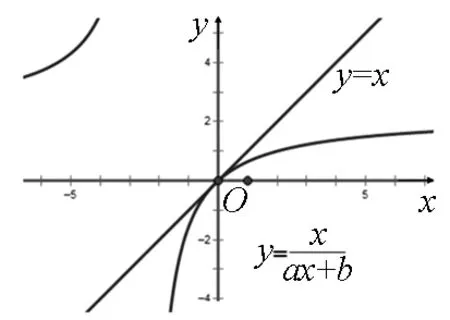
圖2
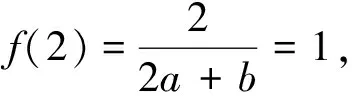
針對思路1,筆者在課堂上對學生提出建議:回顧對于上述過程中每一步,能否確認沒有遺漏任何尚未考慮的情形?
經過充分的觀察與思考后,有學生發現了盲點
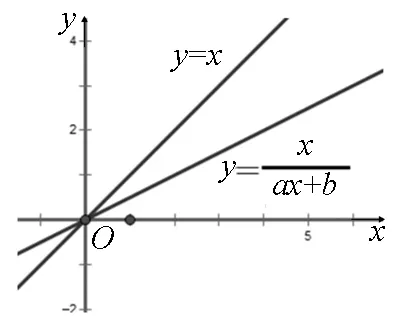
圖3
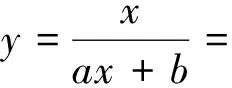
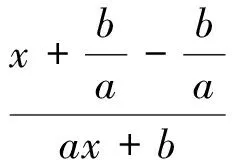
到這里,大家以為可以大功告成時,筆者再次提醒:其它步驟中能確認沒有遺漏任何情形了嗎?
……
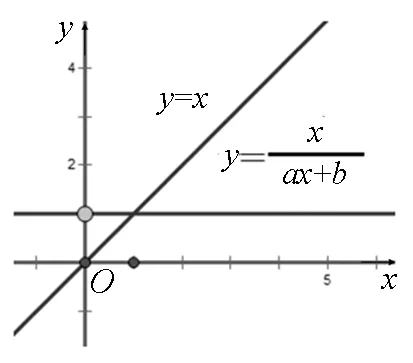
圖4
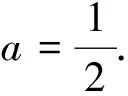
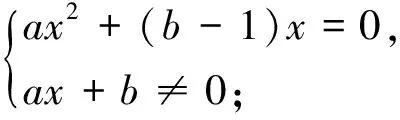
盲點2——第二步ax2+(b-1)x=0有唯一解,故Δ=(b-1)2=0,忽視了二次項系數是否為零;故應補充a≠0的條件;盲點3——對于Δ=(b-1)2≠0時,若方程的非零根恰為方程ax+b=0的根,即為f(x)=x的增根,則方程f(x)=x仍有唯一解.分析了上述思維盲點,解題過程可以整理為如下:
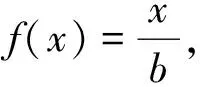
2.當a≠0時,f(x)=x即為
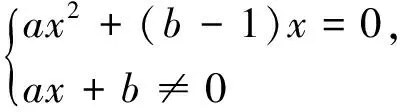
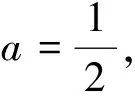
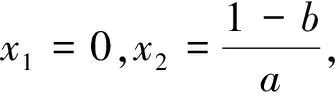
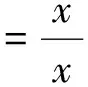
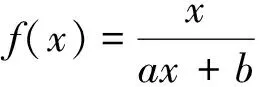
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
小哥白尼(野生動物)(2022年6期)2022-08-17 08:05:28
小哥白尼(野生動物)(2022年4期)2022-07-16 03:37:32
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小哥白尼(野生動物)(2022年2期)2022-06-01 06:21:20
小哥白尼(野生動物)(2022年1期)2022-04-26 14:01:18
美食(2022年2期)2022-04-19 12:56:24
少兒美術·書法版(2021年10期)2021-10-20 06:14:10
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
甘肅教育(2020年12期)2020-04-13 06:24:48

