兩參數對數正態分布與威布爾分布的近似極大似然估計

顧蓓青，徐曉嶺，王蓉華

（1.上海對外經貿大學 統計與信息學院，上海 201620；2.上海師范大學 數理學院，上海 200234）

0 引言

在可靠性試驗中，逐步增加的Ⅱ型截尾壽命試驗在實際中經常會碰到，具有理論與應用價值，而在國內外對此場合卻很少有人進行研究，目前主要是研究定數及定時截尾場合下Weibull分布參數的點估計和區間估計。譬如當組織一批價值昂貴的產品做壽命試驗時，若已有一部分產品失效發生時，考慮到試驗費用等因素，經常會從未失效的產品中抽取一部分產品移離試驗現場，這樣可以大大節約成本。又例如在壽命試驗過程中為了解產品的失效機理和退化情況，以便更好地設計產品，需要從尚未失效的產品中選取部分產品進行解剖分析。再例如觀察患某種疾病的病人的生存情況時，醫生可能僅僅觀察到一部分病人的生存壽命，而另一部分患者可能不到醫院來就診而無法了解其生存壽命，即這一部分病人失去觀察。

逐步增加的Ⅱ型截尾試驗是Ⅱ型截尾的一個推廣，它是在n個產品的樣本中先觀察到r1個失效，然后剩下的n-r1個未失效的產品中有n1個被移離試驗，留下n-r1-n1個產品繼續試驗，當再有r2-r1個產品失效后,將剩余仍未失效產品中的n2個被移離試驗，試驗如此進行下去，直到有一定數量的產品失效為止就終止試驗，試驗數據如表1所示。

表1 逐步增加的Ⅱ型截尾壽命試驗數據

其中r0=0，n0=0，x(0)=0，ri≥1，ni≥0，i=1，2，…，k，k≥1，而nk為最后試驗結束時未失效的產品數。特別地，（1）當ni=0，i=1，2，…，k-1時，便為通常的定數截尾壽命試驗；（2）當r1=1，r2=2，…，rk=k時，通常稱為逐次截尾。

徐曉嶺和王蓉華（2003）[1]給出Weibull分布在逐步增加的Ⅱ型截尾壽命數據參數的極大似然估計與逆矩估計，并通過Monte-Carlo模擬考察了估計的精度，認為極大似然估計優于逆矩估計。王炳興（2004）[2]討論了Weibull分布基于定數逐次截尾壽命數據的參數估計，得到了參數的逆矩估計量和區間估計，模擬結果顯示在中小樣本情況下所給估計量優于參數的最大似然估計。李鳳等（2008）[3]基于逐步增加的II型截尾，討論了Weibull分布的Bayes估計，在平方損失和LINEX損失下，利用Lindely Bayes近似算法得到了形狀參數、尺度參數、失效率函數以及可靠度函數的極大似然估計和Bayes估計，并運用Monte-Carlo方法對各估計結果的RMSE，進行了模擬比較，表明了LINEX損失下的結果更有效。李中恢（2012）[4]在逐步II型截尾樣本下討論了逆Rayleigh分布參數的估計問題，給出了參數的最大似然估計，并在三種不同的損失函數下給出了參數的Bayes估計和區間估計。李瓊和武東（2012）[5]對Pareto分布場合逐步增加II型截尾樣本進行了貝葉斯分析，利用馬爾可夫鏈蒙特卡羅方法給出了參數的貝葉斯估計，并通過蒙特卡羅模擬和應用實例表明該貝葉斯估計是有效的。衛超和師義民（2014）[6]基于逐步II型混合截尾壽命試驗數據，導出了Pareto分布參數的極大似然估計和不同先驗分布下的Bayes估計，并利用Monte-Carlo模擬方法對估計的結果進行了對比分析。楊君慧等（2014）[7,8]基于逐步增加II型截尾試驗，在單參數情況下，利用極大似然估計方法給出了廣義指數分布形狀參數和可靠度函數的極大似然估計，并證明了極大似然估計的相合性和漸近正態性。以及在熵損失和加權平方損失函數下，給出參數和可靠度函數的貝葉斯估計，并運用Monte-Carlo方法對估計結果進行了模擬比較。

此外，文獻[9]中指出，對于一些分布，如指數分布、Rayleigh分布、Weibull分布的參數極大似然估計并沒有顯示表達式。因此，為了改進極大似然估計方法，提出了近似極大似然估計的方法。王蓉華等（2000）[10]給出了在定數截尾數據缺失場合下兩參數對數正態分布參數的近似極大似然估計。顧益明（2011）[11]給出了單參數指數、兩參數指數、兩參數Weibull及兩參數對數正態分布型產品在基于分組型數據下參數的近似極大似然估計。楊振海和程維虎（2004）[12]討論了基于Logistic總體II型截尾樣本分布參數的近似極大似然估計。王娟和陸志峰（2008）[13]針對對數正態分布的一般II型逐步刪失樣本，從似然方程出發，采用一種近似方法將非線性部分線性化求解極大似然估計，并同經典的牛頓迭代法進行數值比較，結果基本相同，表明該方法是一種較好的求參數估計值的方法。張莉（2009）[14]基于指數分布下的分組數據，研究了步加試驗中參數的近似極大似然估計方法，并通過蒙特卡羅模擬說明方法是可行且有效的。

近似極大似然估計方法涉及到函數在點ξi處一階泰勒展開，其中ξi滿足F(ξi)=pi，在定數截尾試驗下而在逐步增加Ⅱ型截尾試驗下，本文考慮l=1，2，…，k或者兩種泰勒展開方式（分別記為方法一和方法二），分別給出兩參數對數正態分布和威布爾分布的近似極大似然估計，并在這兩種泰勒展開方式下比較近似極大似然估計的精度，通過Monte-Carlo模擬發現后者更優。

1 對數正態分布的近似極大似然估計

假設有n個產品進行壽命試驗，產品的壽命X服從兩參數對數正態分布，即X～LN(μ，σ2)，其分布函數FX(x)和密度函數fX(x)分別為：

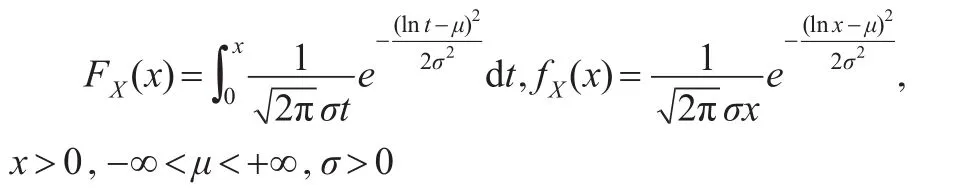
其中μ，σ2分別稱為對數均值和對數方差。

若令Y=lnX，則Y～N(μ，σ2)，其分布函數FY(y)和密度函數fY(y)分別為：

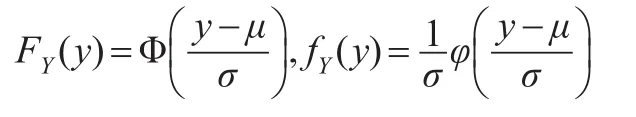
將n個壽命服從兩參數對數正態分布LN(μ，σ2)的產品做逐步增加的II型截尾壽命試驗，試驗數據如表1所示。

令y(i)=lnx(i)，i=1，2，…，r1，…，rk，依賴于數據y(1)，y(2)，…，y(r1)，…，y(rk)的似然函數為：

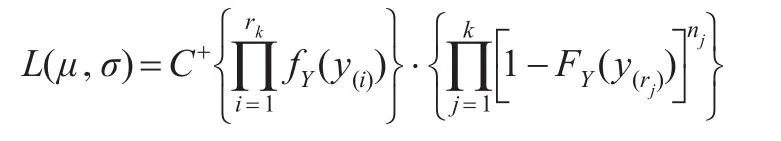
由此：

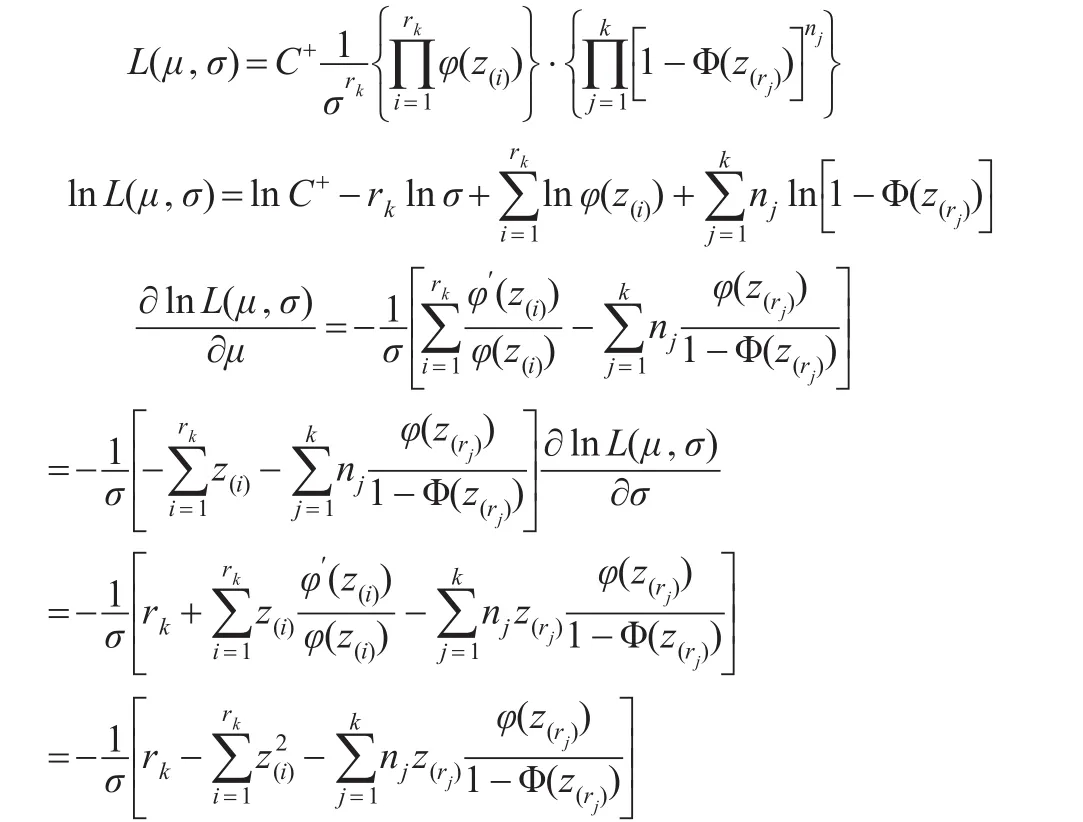
記ξi滿足 Φ(ξi)=pi，i=1，2，…，rk，即ξi=Φ-1(pi)，i=1，2，…，rk

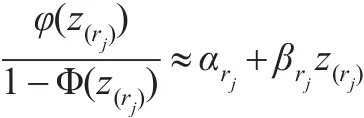
其中：

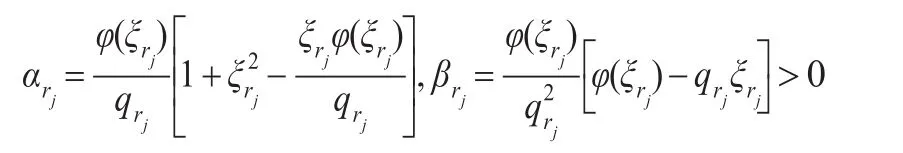
此時有：

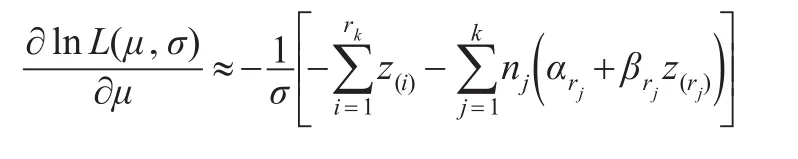
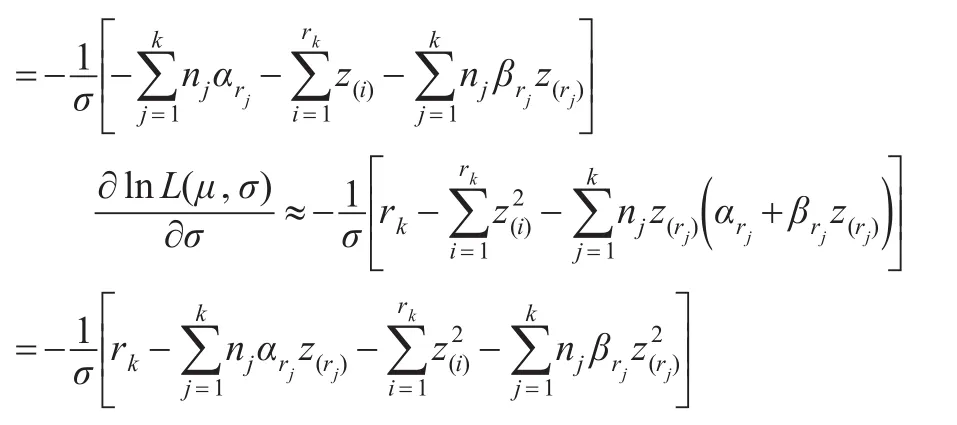
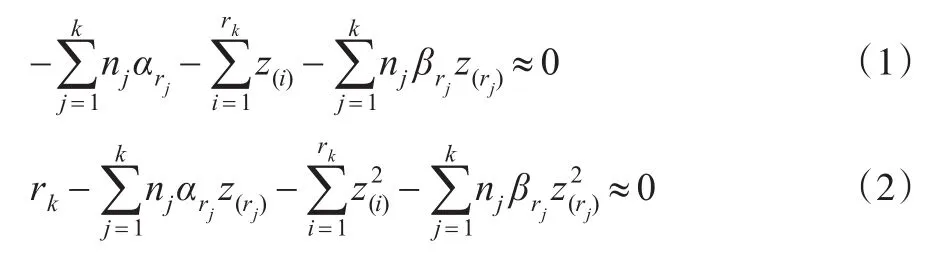
化簡式（1）：

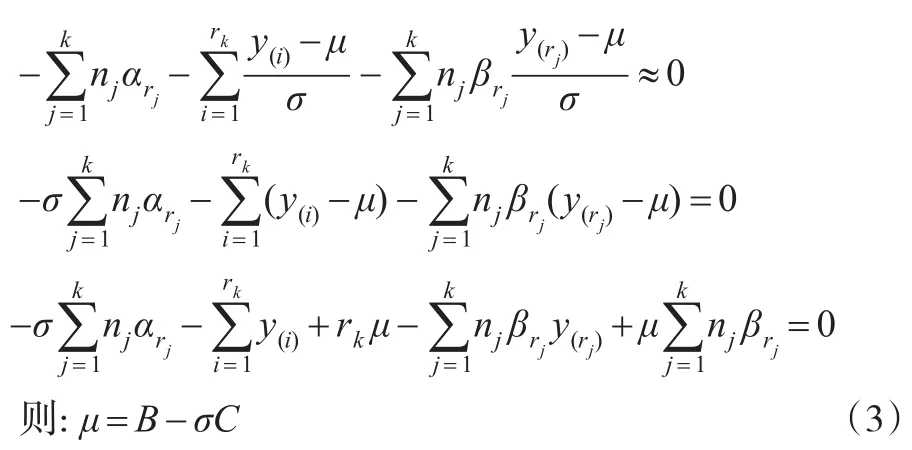
其中：

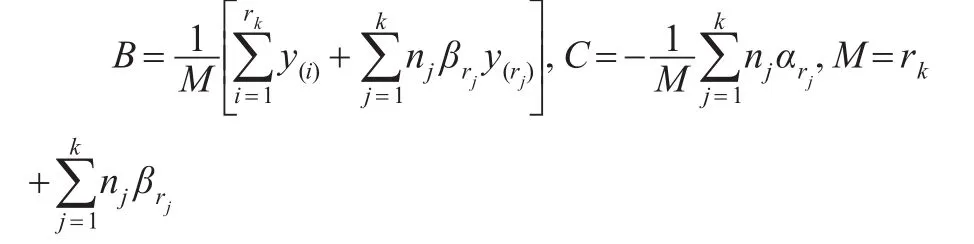
將式（3）代入式（2）化簡得：

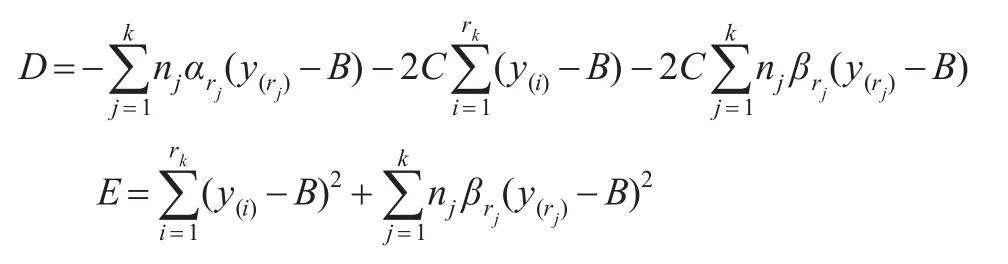
此時方程變形為：Aσ2+Dσ-E=0

則參數σ的近似極大似然估計為：

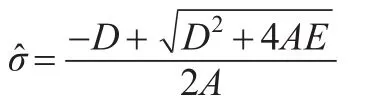
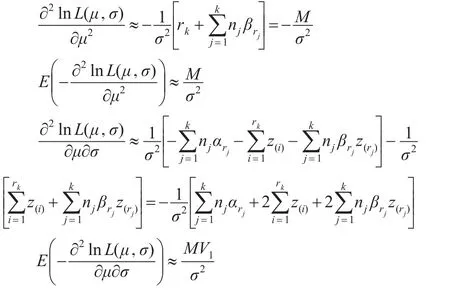
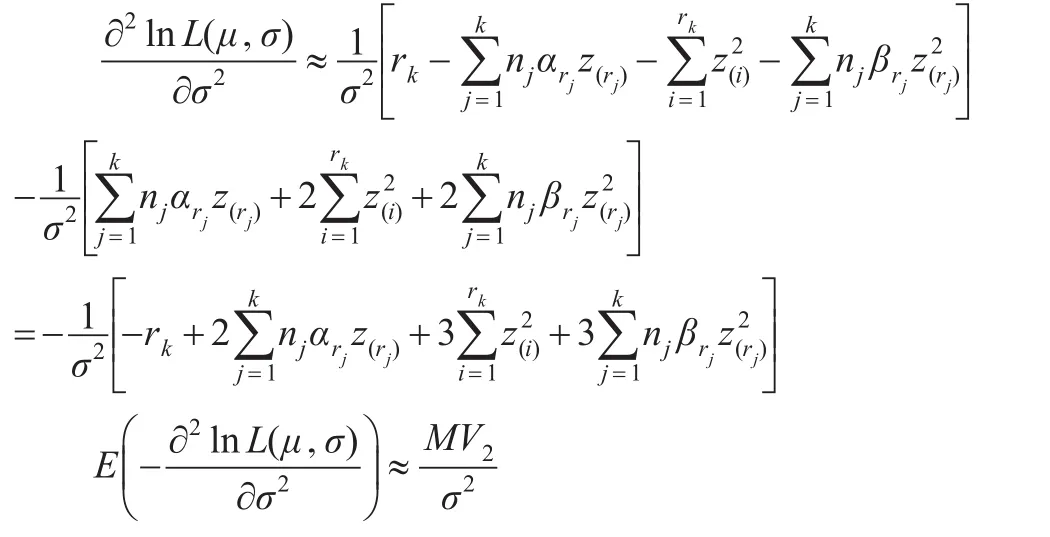
其中：

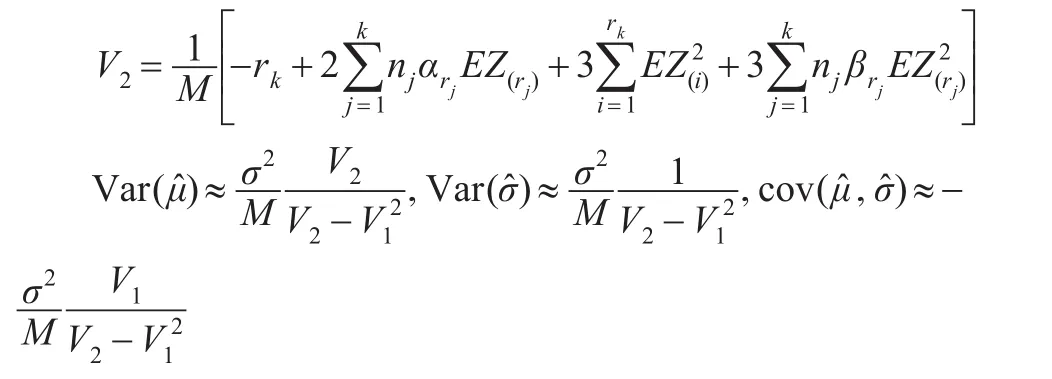
2 威布爾分布的近似極大似然估計

假設有n個產品進行壽命試驗，產品的壽命X服從兩參數威布爾分布，即X～W(m，η)，其分布函數FX(x)和密度函數fX(x)分別為：

其中m＞0為形狀參數，η＞0為刻度參數。

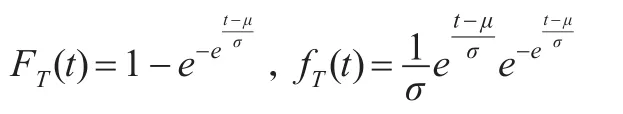
Z的分布函數FZ(z)和密度函數fZ(z)分別為：

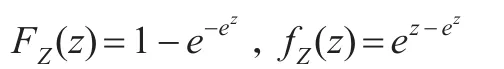
將n個壽命服從兩參數Weibull分布W(m，η)的產品做逐步增加的II型截尾壽命試驗，試驗數據如表1所示。

令T(i)=lnX(i)，t(i)=lnx(i)，i=1，2，…，r1，…，rk，依賴于數據t(1)，t(2)，…，t(r1)，…，t(rk)的似然函數為：

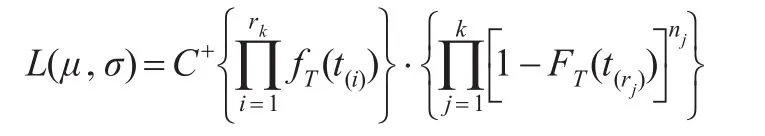
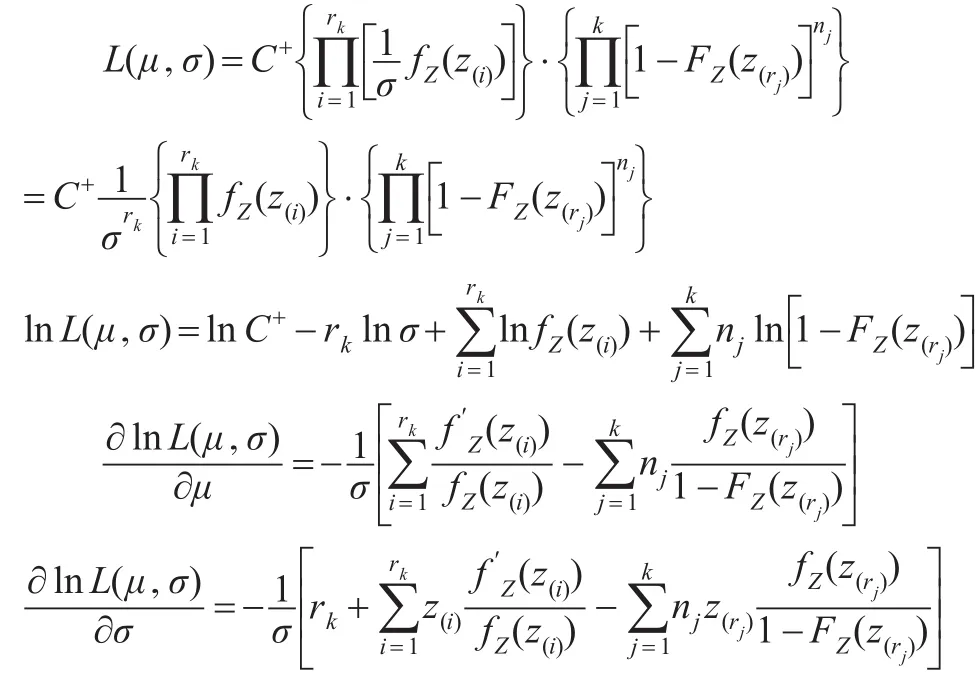
記ξi滿足FZ(ξi)=pi，i=1，2，…，rk，即：

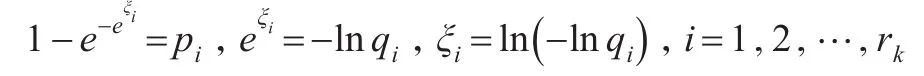
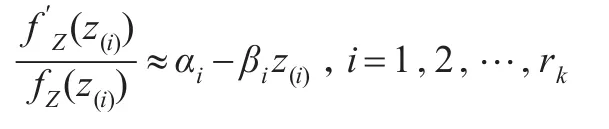
即：

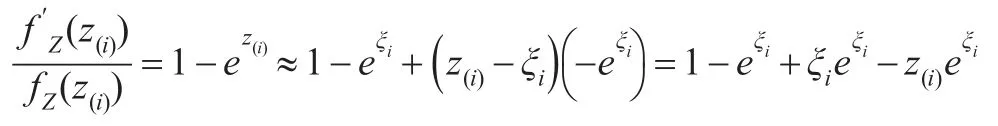
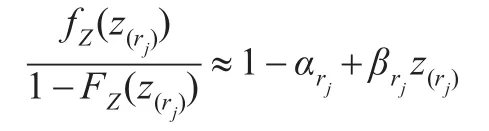
此時有：

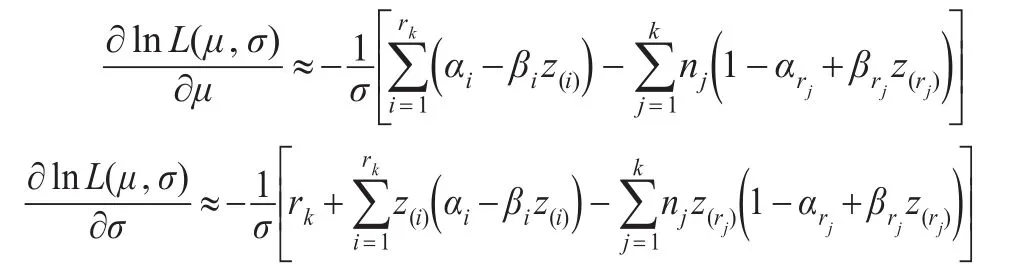
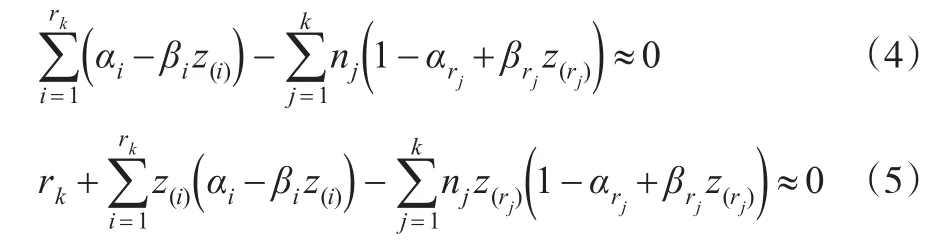
化簡式（4）：

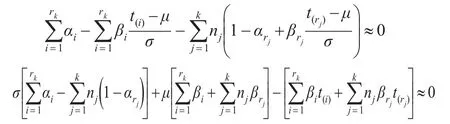
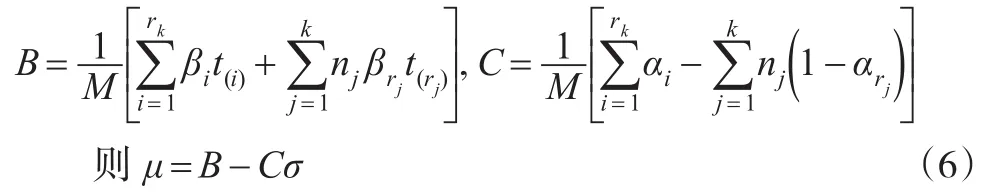
將式（6）代入式（5）化簡得：

記：

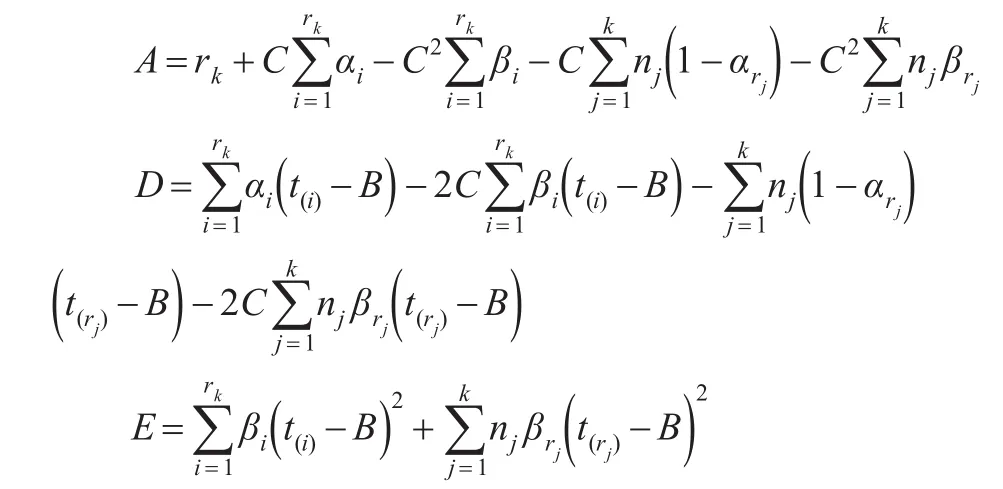
此時方程變形為：Aσ2+Dσ-E=0

則參數σ的近似極大似然估計為：

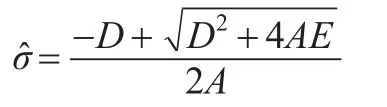
因此，參數η和m的近似極大似然估計分別為：

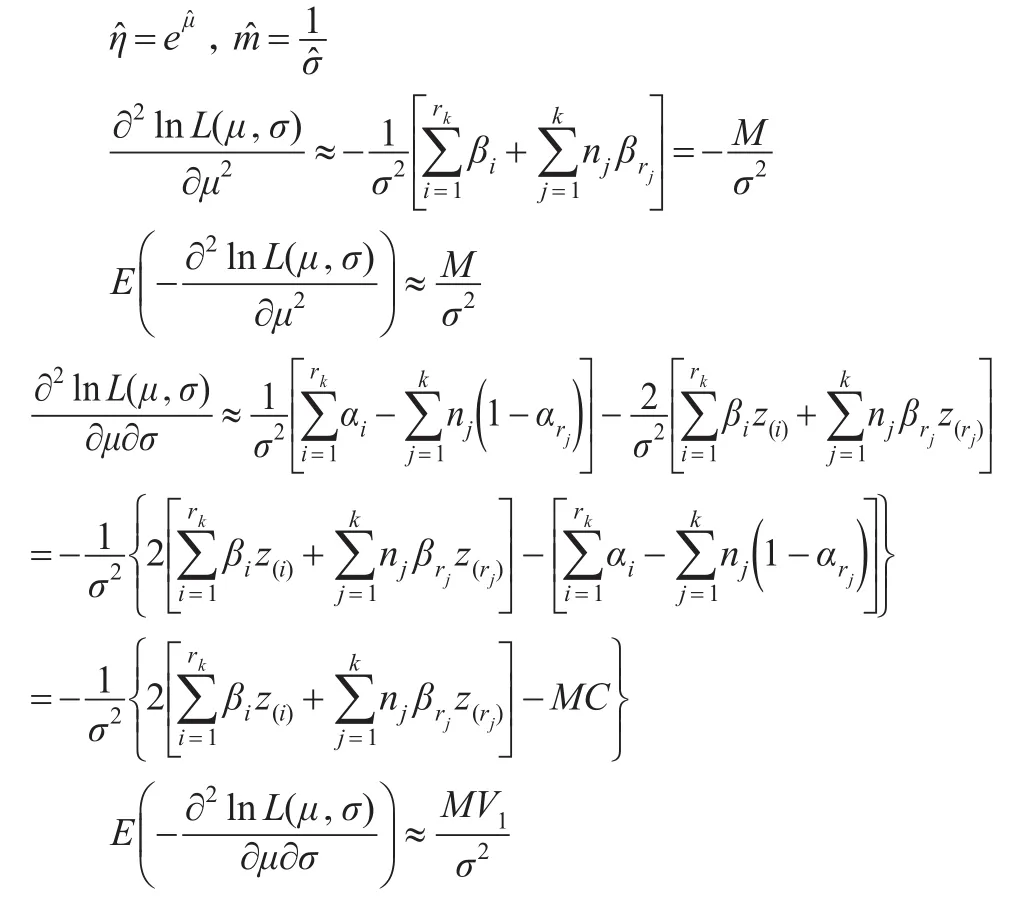
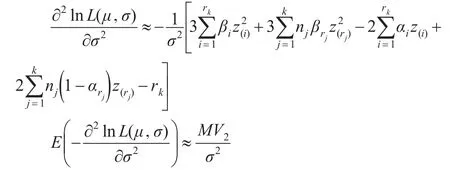
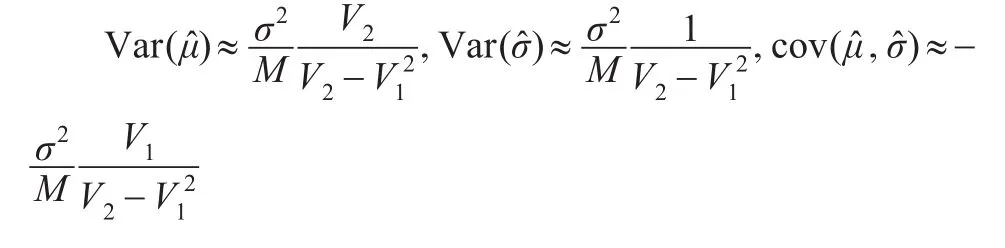
3 模擬比較及算例

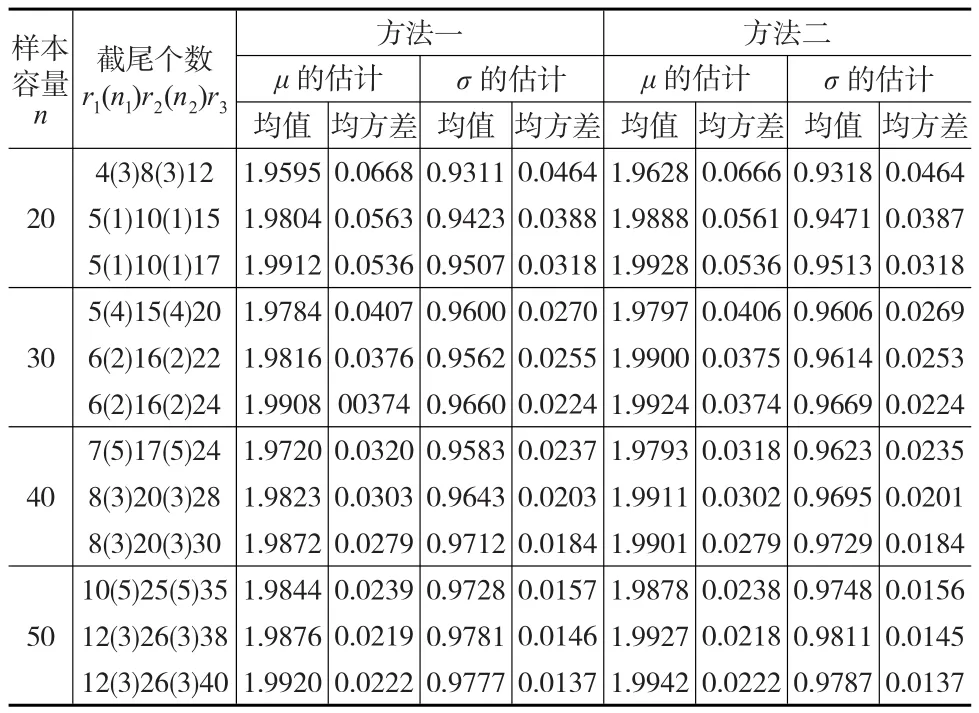
表2 對數正態分布的近似極大似然估計比較

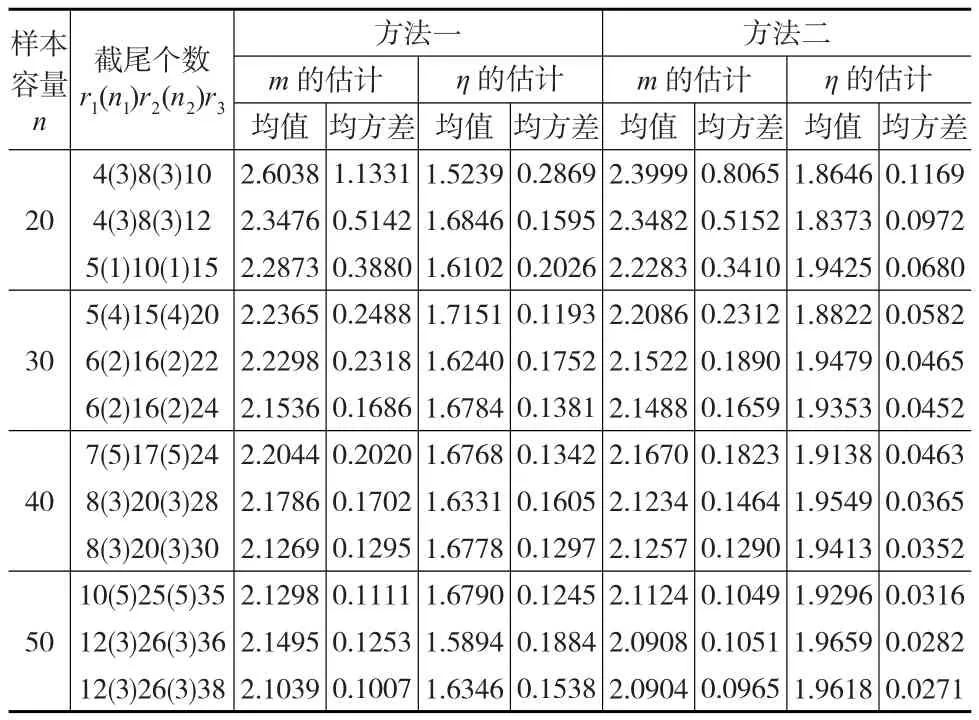
表3 威布爾分布的近似極大似然估計比較

例 1：取對數正態分布LN(μ，σ2)的參數真值為μ=1，σ=1，樣本容量n和截尾個數為n=20，r1=5，n1=2，r2=10，n2=2，r3=15，通過Monte-Carlo模擬產生逐步增加的Ⅱ型截尾樣本數據為：-1.4247，-0.6394，-0.3934，0.1061，0.2061，0.6364，0.7162，1.0006，1.0378，1.0543，1.0669，1.1496，1.4043，1.4488，2.1458，利用本文方法，由方法一得到參數μ，σ的近似極大似然估計為μ?1=0.9136，σ?1=0.9920 ，由方法二得到參數μ，σ的近似極大似然估計為μ?2=0.9167，σ?2=0.9926 。

例2：取威布爾分布W(m，η)的參數真值為m=2，η=1，樣本容量n和截尾個數為n=30，r1=8，n1=4，r2=15，n2=3，r3=20，通過Monte-Carlo模擬產生逐步增加的Ⅱ型截尾樣本數據：-2.5044，-1.2816，-0.9434，-0.9004，-0.8201，-0.7804，-0.7768，-0.7563，-0.6990，-0.3452，-0.3081，-0.2960，-0.1561，-0.1545，0.0164，0.1370，0.1512，0.2321，0.2412，0.2873，利用本文方法，由方法一得到參數m，η的近似極大似然估計為m?1=2.0759，η?1=0.8549 ，由方法二得到參數m，η的近似極大似然估計為m?2=1.9820，η?2=1.0226。

4 結論

在推導參數近似極大似然估計的過程中會關系到函數的一階泰勒展開，本文在逐步增加Ⅱ型截尾壽命試驗下考慮了兩種泰勒展開方式，并且針對兩參數對數正態分布和威布爾分布分別推導了參數的近似極大似然估計，并在這兩種泰勒展開方式下比較了估計的精度，通過大量的Monte-Carlo模擬發現利用方法二的泰勒展開方式得到的近似極大似然估計略優。