分形視角下期現套利策略：基于“股災”數據的實證

朱鵬飛，唐 勇

（1.福州大學 經濟與管理學院，福州 350116；2.金融數學福建省高校重點實驗室（莆田學院），福建 莆田 351100；3.福建省金融科技創新重點實驗室，福州 350116）

0 引言

2015年下半年的大熊市中接連出現三次“股災”，導致大部分投資者賬面資金損失慘重，信心喪失。對投資者而言，與單方向的投資行為相比，套利活動具有更小的風險、更穩定的收益以及更高的夏普比率等優勢。如何構建在“股災”般極端波動環境下行之有效的套利策略一直是金融學術界和實務界關注的熱點話題。

以往諸多國內外學者[1-3]基于協整框架，對套利策略進行了相關研究，證明其是行之有效的。另外一部分學者[4-6]將Copula函數族引入到協整框架中，然而基于Copula函數族忽略了金融市場不同時間標度的豐富價值。作為挑戰傳統學術界的新興前沿課題，以分形理論等為代表的復雜非線性金融物理學科越來越受到主流金融學界的關注，國內外諸多學者[7-9]運用分形理論方法研究金融市場間復雜性問題，成果較多。但實際研究大徑相同，都只是對市場間復雜特征進行分析，并沒有與傳統金融實踐理論等方面形成有效銜接，制約了分形理論在實際中的應用。鑒于此，本文基于Kristoufek[10]的單分形回歸框架，構建了單分形期現套利策略，實現分形理論與傳統套利理論的結合。同時，針對單分形的不足[11]，本文在消除趨勢波動分析回歸框架基礎上提出了多重分形消除趨勢波動分析回歸框架，并基于此，構建多重分形套利策略，將其用于本輪大熊市中。

1 理論框架

1.1 DCCA方法

消除趨勢交叉相關性分析（Detrended Cross-Correlation Analysis，DCCA）方法主要是研究兩個非平穩時間序列在不同時間標度下的非線性關系，但是該方法存在偽波動的缺陷[11]。鄭輝和王斌會[12]認為可以通過重疊平滑窗技術對原始方法優化，克服該缺陷。因此，本文基于其優化思想，以{xi}和{yi}表示兩個時間序列，i=1,2,…,N，N為序列的長度，構建優化后的DCCA方法。建模步驟如下：

第一步，計算累積離差序列：

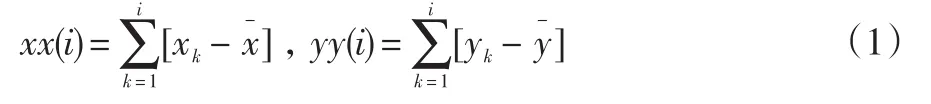
其中：、分別為原始序列{xi}和{yi}的均值。

第二步，將序列{xx(i)}和{yy(i)}分割成標度為s的Ns=[(N-s)/(s-l)]（[]表示取整數）個區間，重疊長度為l，

第三步，對于每個區間v(v=1,2,…,2Ns)，進行消除趨勢處理，最終消除局部趨勢，得到殘差序列：

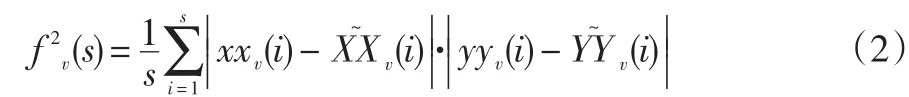
第四步，計算各個標度的協方差函數：

第五步，如果冪律相關性存在，則標度關系滿足如下條件：

1.2 MF-DCCA方法

多重分形消除趨勢交叉相關性分析（Multifractal Detrended Cross-Correlation Analysis，MF-DCCA）方法的步驟一到步驟三與DCCA方法相同，在此不再贅述。從第四步開始介紹：

第四步，計算q階波動函數：

人力資源和社會保障部推出的《2017年度人力資源和社會保障事業發展統計公報》顯示，我國參加城鎮職工養老保險的農民工人數僅占農民工總人數的21.6%，參加城鎮職工醫療保險的農民工人數占農民工總人數的21.7%，參加城鎮職工失業保險的農民工人數占農民工總人數的17%，參加城鎮職工工傷保險的農民工人數占農民工總人數的27%。目前我國失業率居高不下的形勢下，農民工失業保險參保率遠低于工傷、醫療和養老保險參保率，失業保險參保概率不足。因此，新生代農民工養失業老保險作為推進新型城鎮化重要方面，解決好這一問題體現新型城鎮化“以人為本”的發展核心。

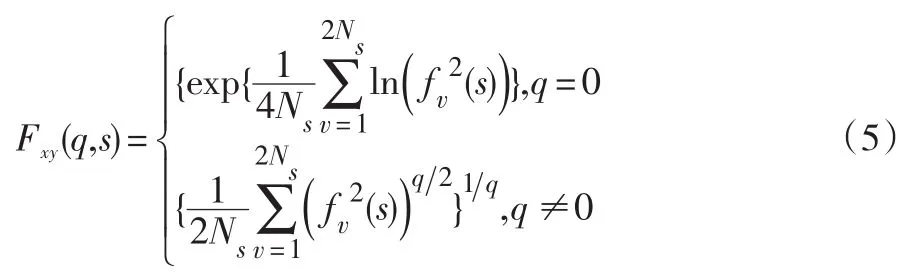
第五步，如果冪律相關性存在，則標度關系滿足如下條件：

當q=2時，MF-DCCA方法轉換為DCCA方法。當兩個時間序列相同時,即{xi}={yi}，MF-DCCA方法轉變為多重分形消除趨勢波動分析（MF-DFA）方法，故不對MFDFA方法單獨進行介紹。

1.3 消除趨勢波動分析回歸框架

Kristoufek[10]提出的消除趨勢波動分析回歸框架能夠對兩個非平穩的時間序列的不同時間標度和冪律相關關系進行準確刻畫和描述，有效地克服了傳統統計套利模型的缺陷，充分利用了多時間標度的價值。該回歸框架如下：

a是長期合理的價差，ut是均值為零的殘差序列，也可以被認為是噪聲部分，β(s)可以描述在不同時間標度下，兩個變量之間的非線性冪律相關關系，公式如下：

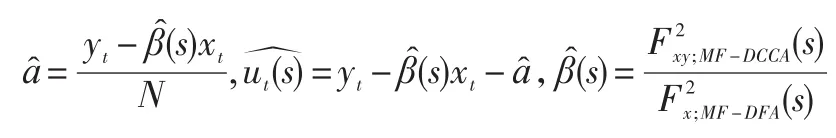
其中，F2x,y;DCCA(s)、Fx;DFA(s)由公式（3）計算可得。

1.4 多重分形消除趨勢波動分析回歸框架

單分形無法對局部進行全面精確的刻畫和分析，多重分形模型則可以從復雜的運行過程中尋找金融市場的內在規律[11]。因此，本文擴展Kristoufek[10]的研究，提出多重分形消除趨勢波動分析回歸框架：

假設{xt}和{yt}其滿足如下關系：

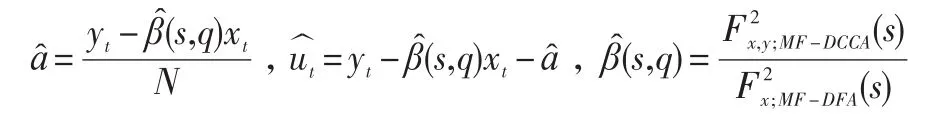
其中，s表示標度，q表示階數，也即波動幅度。當q＜0，則是對小幅波動的刻畫，當q＞0，則是對大幅波動的刻畫。Fx;MF-DFA(s)、Fx,y;MF-DCCA(s)可以分別通過公式（5）計算得到。

2 實證分析

2.1 數據選取和處理

三次“股災”發生在2015年6月8日至2016年3月1日期間，根據文獻[13]，該段區間又可以被認為是熊市。因此，選定2015年6月8日至2016年3月1日作為樣本區間。本文在此選擇滬深300指數作為股票市場的代表，選擇5分鐘收盤價作為樣本數據。最終得到期貨和現貨各自8400個樣本。對區間內期貨和現貨價格序列進行統計描述。

表1 期貨和現貨市場價格序列統計

表1顯示，期貨和現貨價格序列“尖峰肥尾”特征顯著，各個序列的JB統計量在1%的顯著性水平下拒絕服從正態分布的原假設。同時，在滯后40階數時，各個序列的自相關性顯著。ADF單位根檢驗結果表明各個序列都是非平穩的。

2.2 交易規則制定

本文在此把滬深300ETF作為滬深300指數的替代交易工具。設期貨價格序列為yt，現貨價格序列為xt，殘差序列為ut，制定交易規則如下：

（1）若ut大于閾值x1（小于閾值x3）時，認為期貨合約被高估（低估），現貨被低估（高估）。因此，套利開倉，賣出（買入）N份期貨合約，同時將N·β(s·)x·t300的資金用于購買（賣出）滬深300ETF。（2）當ut回到均衡值x2附近時，價差回到了均衡位置，進行與（1）相反操作，進行獲利平倉。（3）為控制交易過程中的風險，當ut大于x4或者小于x5時，進行止損平倉。若當日已進行止損平倉操作，或者出現空倉時ut大于x4、小于x5極端情況，為避免造成損失或者損失擴大，當日不再進行交易，次日繼續進行套利活動。

設置x1=0.75σ、x2=0、x3=-0.75σ、x4=2σ、x5=-2σ。同時，設2015年9月7日前滬深300股指期貨采用12%的保證金比例，在此之后，采用40%的保證金比例。設定現貨的手續費為0.08%，期貨的手續費為0.05%。同時設定現貨市場可以通過融券業務進行賣空，但是不考慮使用資金杠桿。

2.3 熊市樣本內外區間劃分

為了更好地檢驗本文的單、多重分形套利模型的優越性，在此參照文獻[14]，將整個熊市劃分為樣本內區間和樣本外區間，以樣本內區間數據估計參數，構建套利模型，然后利用其在樣本外區間進行套利活動。劃分如表2所示。

表2 樣本內區間和樣本外區間的劃分

2.4 單分形套利策略回測檢驗

在此基于Kristoufek[10]的消除趨勢波動分析回歸框架構建單分形套利策略，選擇s取值范圍為100～900，步長為100，共9個標度。本文把傳統的協整套利策略作為參照組，采用的是Engle-Granger方法，模型具體見文獻[14]，此部分估計詳細結果由于篇幅限制，不在此展示。接下來在樣本外區間進行套利回測檢驗，對單分形套利模型和協整模型進行比較，樣本外檢驗結果如表3所示。

表3 樣本外區間套利結果

從表3中可得，在熊市中傳統的協整套利策略收益為負數，給投資者造成了一定的損失，這說明傳統的套利策略并不能在波動劇烈的熊市中為投資者帶來滿意的收益。與其形成鮮明對比，大部分標度的單分形策略優于對照組，取得更高的收益率、套利成功率和夏普比率，說明單分形套利策略能夠取得較好的套利效果。同時，標度的不同也會對套利效果產生一定的影響。

2.5 多重分形套利策略回測檢驗

基于本文提出的多重分形消除趨勢分析回歸框架，構建多重分形套利策略，并將其應用在“股災”般異常波動的熊市環境中，檢驗其可行性和優勢性。考慮到本文采用的q階范圍為-10～10（不含0），步長為2，由于篇幅限制，不給出各個q階的參數估計結果。以單分形套利策略作為參照組進行對照比較，檢驗結果如表4所示。

由表4可知，當q=-2時，存在5組標度優于單分形套利策略，由此證明本文提出的多重分形套利策略通過選擇合適的q階，與單分形策略相比，能夠為投資者提供更優的組合方案。此外，最優q階的多重分形套利策略有5組標度明顯優于單分形套利策略。

表4 表現最佳q階檢驗結果

3 結論

本文基于分形視角，以消除趨勢波動分析回歸框架為依據，構建了單分形套利策略。考慮到單分形理論的不足，又提出了多重分形消除趨勢波動分析回歸框架，構建了多重分形套利策略。將單、多分形套利策略運用在2015—2016年大熊市真實環境中，具體結論如下：

（1）基于Kristoufek[10]提出的消除趨勢波動分析回歸框架，構建單分形套利策略，與傳統的協整套利策略進行樣本外區間套利效果比較。結果表明，在熊市中，大部分標度的單分形套利策略優于傳統協整套利策略。同時不同標度的套利效果存在明顯的差異。

（2）本文提出了多重分形消除趨勢波動分析回歸框架，并構建了多重分形套利策略，與單分形套利策略進行樣本外區間套利效果比較。結果表明，當q=-2時大部分標度的套利效果最佳。以上套利結果也表明，基于本文提出的多重分形消除趨勢波動分析回歸框架，構建多重分形套利策略是有效的。