矩陣正態總體下均值估計改進的新方法

劉 薇

（湖南財政經濟學院 數學與統計學院，長沙 414205）

1 問題的提出

考慮模型：

這里假設X與S獨立，Θ是m×p階未知總體正態均值矩陣，C是已知的m階正定矩陣，Σ是p階的未知協方差陣，Wp(Σ，k)表示自由度為k，均值為kΣ且維數為p的Wishart分布，符號?表示矩陣之間的Kronecker乘積，對于方陣A，A＞0表示A是正定矩陣，A≥0表示A是非負定矩陣。模型（1）可看做是MANOVA模型或者多元線性模型[1,2]。

其中權重Q是任意給定的非負定陣。對于Θ的一個估計?和式（2），本文定義?的風險為：

基于充分統計量(X，S)并把Σ看做冗余參數，本文將在式（2）下研究均值矩陣Θ的估計的改進問題，并把相關結果應用到協方差的估計的改進問題中去。顯然，模型（1）中參數矩陣Θ的最大似然估計是=X。對于Θ的任意一個估計?，如果RW(?，Θ)≤RW(，Θ)，本文稱是最小最大估計。事實上，許多文獻考慮了模型（1）中Θ的估計問題。比如：文獻[3]考慮了m=1，Q=Im且Σ已知的情形；在Σ未知的情況下，文獻[4]處理了m=1，Q=Im的情形；文獻[5]研究了p=1，Q=Im且 Σ=σ2（σ2未知）的情形；在Σ未知的情況下，文獻[1]考慮了m＞p+1，Q=Im的情形；在Σ未知的情況下，文獻[2]考慮了p＞m+1，Q=Im的情形。上述文獻都假設權重Q為單位陣，但是除了文獻[6，7]幾乎沒有相關文獻處理Q≠Im情形。然而，權重Q的引入不僅推廣了已有的結果，更為重要的是它揭示了均值矩陣估計與協方差陣估計之間的本質關系。文獻[8，9]指出了這種關系但他們并沒有作進一步的研究。而文獻[6]研究了這個問題，但是文獻[6]利用正態分布和Wishart的性質僅考慮了Q為對角陣且m＞p+1的情形。而這種方法很難用來處理p＞m+1的情形。本文將解決這個問題，同時假設Q是任意給定的非負定陣，C是已知的正定陣。本文的主要目的是推廣已有文獻中的結論。為了加強本文結果的有用性，本文的方法可以用來進一步改良文獻[6]中第三部分的結果，因為文獻[6]僅考慮了m＞p+1的情形下均值估計和協方差估計的關系。

2 Efron-Morris估計的新方法

為了在p＞m+1的情形下和更廣義損失下改進矩陣均值估計，本文考慮著名的Efron-Morris估計。為了展示在更廣義損失下Efron-Morris估計是最小最大估計，需要導出相應風險的無偏估計，這種無偏風險比已有文獻中的結果更復雜。在模型（1）下，考慮如下的Efron-Morris估計：

當Q=C=Im時，在式（2）下，文獻[2,9]獲得了α的最優解為：

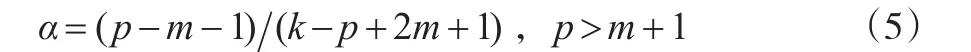
當C=Im,Q:=W=diag(w1，…，wm)時，文獻[6]考慮了m＞p+1情形下的Efron-Morris估計，并導出了α的最優解，即：

但是他們沒有考慮p＞m+1下Efron-Morris估計的改良問題。本文只要求在C＞0，Q≥0的假設下，研究在p＞m+1情形下的Efron-Morris估計。本文的結果推廣了已有的結論。

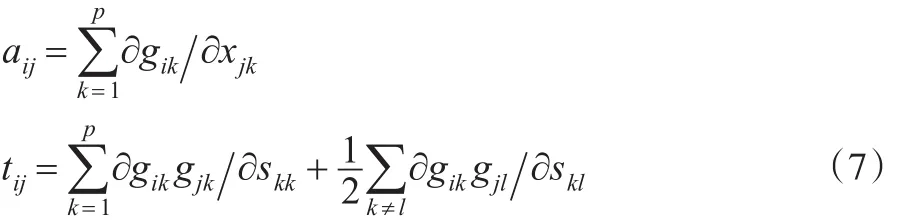
為了獲得本文的主要結果，需如下的引理：

引理 1：設對稱矩陣A1，B1，C1∈Rn×n的特征根分別為a1≥…≥an，b1≥…≥bn和c1≥…≥cn，則：

①若A1≥0，B1≥0，C1≥0，有：

②若A1＞0，B1＞0，C1＞0，有：

證明：對于①的證明見文獻[10]中的定理3，而②中右邊的不等式可由①直接獲得。因此，只需證明②中左邊不等式。由文獻[11]中引理1和矩陣同時對角化相關知識，知存在一個正定陣B0，使：

而由文獻[12]知，A1B0C1的特征根都是正數。從而引理1成立。

當p＞m+1時，本文把Efron-Morris估計式（4）記為：

這里G2=-α(XS-1X′)-1X，為了避免引入新的記號，令Am×m:=(aij)，Tm×m:=(tij)，F=XS-1X′=RLR′，這里aij和tij與式（7）定義相同，L=diag(l1，…，lm)，RR′=R′R=Im，R是m×m階正交陣，l1≥…≥lm≥0是F=(Fij)的特征值，進一步 ，記 ▽X=(?/?xij) ，DF=((1+δij)/2)(?/?Fij) ，DFg(F)=，這里g(F)是標量，V=V(F)=(vij)是m×q階矩陣，δij是Kronecker算子。類似地，本文可以定義DS、DSg(s)和DSV。

經過簡單的計算，有：

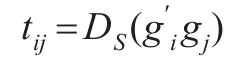
這表明：

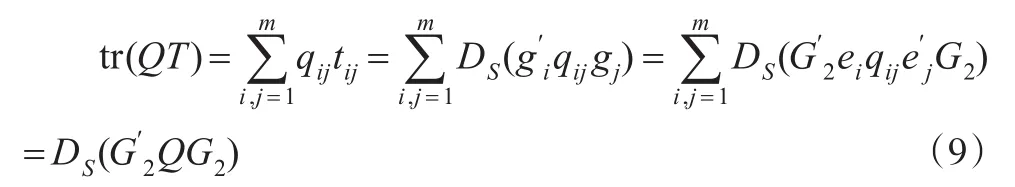
因而，結合式（9）與文獻[1]中的推論2.1知，在式（1）和式（2）下的風險的無偏估計具有如下形式：

本文將利用式（10）并在一定的條件下證明了p＞m+1情形下Efron-Morris估計為最小最大估計。為此，還需要如下引理：

引 理 2：令?(L)=diag(?1(L)，…，?m(L)) ，R=(R1，R2…，Rm)（Ri是相應于特征值li的特征向量），并假設相關偏導數存在，則：

①DFli=Ri，

③DF[R?(L)R′]=R?1(L)R′，

其中：

證明：見文獻[2]中的引理2.3。

令：

從而：

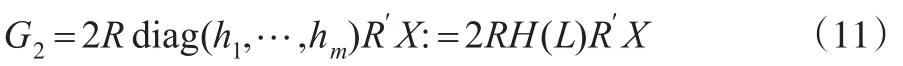
這里H(L)=diag(h1，…，hm)。由文獻[2]中引理2.3得：

進一步，由文獻[2]中的引理2.2知：

結合式（10）至式（12）有：

因此，類似于文獻[2]中定理2.1的證明并經過簡單的計算，無偏風險式（11）可表示為：

顯然，當C=Q=Im時，式（14）即可化簡為文獻[2]中的結果。

定理1：在模型（1）和式（2）下并假設Q＞0，如果α滿足：

證明：由式（12）知：

由引理2和式（13），得：

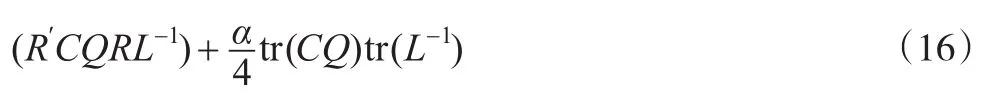
因此，結合式(15）和式（18）知：

由引理1知：

從而定理1成立。

由定理1易知，當C=Q=Im時，α的最優解與文獻[2]一致。

3 實例

本文通過一個數值的例子來驗證定理1中結果的有效性。假設Θ的每個元素是來自均勻分布的某次抽樣，C是一個對角矩陣且每個對角元素是來自標準正態分布的某次抽樣，Σ具有一階自回歸結構且一階系數為0.5，Q具有一階自回歸結構且一階系數為0.5。進一步，在這個例子中取，顯然它滿足定理1中的條件。為了比較，考慮不同的參數組合(m,p,k)，利用2000次蒙特卡洛模擬去計算相關估計的風險，相關結果被描述在表1中。從表1中的數值結果，可以清晰地觀測到改進后的EM估計優于未改進的EM估計和最大似然估計，這與理論分析是一致的。

表1 相關估計的風險結果

4 結束語

本文改良著名的Efron-Morris估計，在C＞0，Q≥0的假設下，研究了p＞m+1情形下的Efron-Morris估計。并在適當條件下，證明了該Efron-Morris估計是極小極大的。值得說明的是，文獻[6]僅考慮了m＞p+1的情形下均值估計和協方差估計的關系，下一步打算用本文的結果在p＞m+1的情形下建立均值和協方差估計的關系。