假設檢驗中T檢驗原理與對比應用

□牛 凱 陳 悅

在假設檢驗原理中T的檢驗原理及對比應用研究就具有很強的實際價值，為了貼近現階段的數學分析課堂教學及教研，本文在數據分析假設檢驗中T檢驗原理與對比應用研究中，依舊是采用單樣本，然后利用T分布統計量和T檢驗統計量的關系，對T檢驗原理及對比應用進行清晰闡述。

一、數據分析假設檢驗中T檢驗原理

假設檢驗是梳理數據中根據相應的假設條件通過樣本推斷出總體的一種方法，所以在假設檢驗中需要對研究總體進行某種假設，也就是原始假設H0，然后在假設H0成立條件下選取合適的統計量，確保其分布為已知，再通過實際樣本測量情況，計算出統計值針對預先給定的顯著性水平進行檢驗對H0進行判斷給出肯定或是拒絕的結果。基于假設檢驗的小概率反證思想，以小概率事件(P<0.01或P<0.05)作為假設依據，利用反證法先提出相應的假設，根據統計方法確定假設成立的可能性大小判斷，可能性大的情況下還需要進行T值的判斷，當測量總體服從正態分布N的(μ，σ2)時，則可以通過T=遵從自由度為n-1的T分布，可以對μ有以下的水平為α的檢驗，基于T檢驗的判斷依據之后才能夠得出判斷結論。T檢驗是利用T分布理論來推測差異發生的概率，應用于數據分析假設檢驗，通過兩個平均數的差異的顯著性進行假設驗證，是由戈斯特發明，起初目的在于觀測釀酒質量，其檢驗效果與f檢驗、卡方檢驗有著異曲同工的用途。

T檢驗的原理是以T分布作為基礎，對一個或者是兩個樣本數據進行假設檢驗的常用方法，也是參數檢驗的一種。是根據各回歸系數的顯著性進行檢驗，在檢驗過程中若是多元回歸則是先針對回歸系數是否為零進行F檢驗，之后再對整體回歸系數進行是否為零的T檢驗，然后根據檢驗樣本的一元正態分布的總體期望也就是均值進行檢測，是否與二元正態分布的總體期望相等。T檢驗的最終目的是為了比較樣本均數所代表的未知總體均數μ和已知總體均數μ0，如此一來就可以避免大量的實驗直接進行假設結果檢驗。

二、T檢驗的對比應用

T檢驗一共分為單總體檢驗與雙總體檢驗，單總體T檢驗是對一個樣本平均數與已知總體平均數的差異的顯著性進行判斷，但總體分布為正態分布時，如果總體標準差未知并且樣本容量低于30的時候，那么樣本平均數與總體平均數的離差統計量則呈現為T分布，雙總體T檢驗是檢驗兩個樣本平均數與其帶包的總體差異的顯著性進行判斷，雙總體T檢驗也存在兩種情況，一是獨立樣本T檢驗，二是配對樣本T檢驗，兩者檢驗的方程并不相同。三個方法中單總體檢驗以及配對樣本T檢驗常用，而配對T檢驗方法在日常和科研中應用較少，所以在教學還是實際使用中比較常用的是單總體T檢驗以及獨立樣本T檢驗法。

(一)單總體檢驗。單總體T檢驗主要是用于研究單個樣體(變量)的均值與假設檢驗值之間的差異顯著性，例如某一個學生成績與班級總體學生成績之間有無顯著差異性？或者本地大學生心理健康水平與全國平均水平有無顯著差異性？單總體檢驗中還有其他的檢驗方式，例如單總體X2擬合優度檢驗，非參數性假設，用于觀察樣本頻數與期望頻數之間的差異顯著性，例如網絡成癮研究視角研究是否存在差異顯著性；單樣本二項檢驗，主要是用于檢驗二分變量樣本中第一類情況出現的比率與總體中該事物出現比率的是否存在差異顯著性，例如合格率的判定。單總體T檢驗的假設判斷依據在于樣本均值與總均值之間的關系，但樣本均值接近總體均值則表示原假設成立，樣本均值與總均值相差很大，則原假設被拒絕，判斷總均值與樣本均值差距的是拒絕域和接受域，跟正態曲線的區域劃分，如圖1所示。

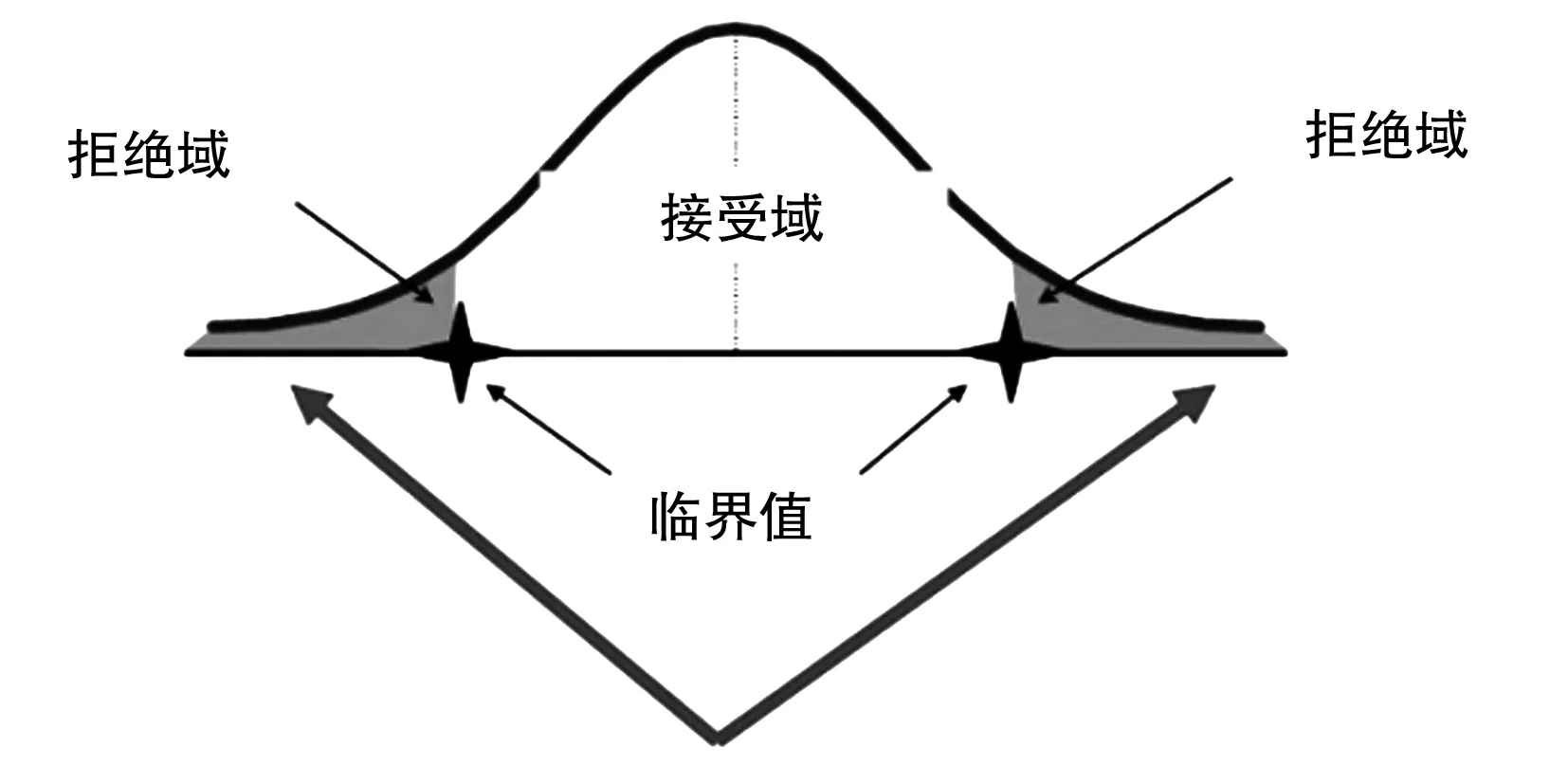
圖1

所以原假設不成立，備擇假設成立。

(二)獨立樣本檢驗。獨立樣本T檢驗，要求兩個樣本之間沒有具體的關系彼此獨立存在，均來自于正態分布，并且均值對檢驗量有意義的描述統計量。例如男女性之間的工資均值比較，其解析步驟為：分析——比較均值——獨立樣本T檢驗。通過兩個獨立樣本存在不同均值之間的差異進行經驗，以檢驗這兩個樣本是否來自于具有相同均值的主體。

1.先進行原假設與備擇假設建立。H0為兩個樣本均值總體無明顯差異，μ1-μ2=0，H1為兩個樣本均值總體存在差異顯著性，μ1-μ2≠0。

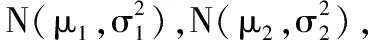
三、結語

總而言之，數據分析假設檢驗中的T檢驗原理是基于T分布來推測發生概率，對比應用主要是針對備擇假設以及原假設，通過兩個假設成立條件以及樣本的組間差距判斷兩者的成立結果，無論是在數學統計課堂教學中還是教研中，都需要注意T檢驗的適用范圍以及限制條件的明確。