表貼式PMSM轉子初始位置非線性估計

雷學國，蔣學程

(1. 福建萬潤新能源科技有限公司，福州350108； 2. 閩江學院，福州 350108)

0 引 言

增量式光電編碼器或無位置傳感器永磁同步電動機(以下簡稱PMSM)在起動控制階段無法確定PMSM轉子初始位置，需要通過算法觀測電機轉子初始位置，保證PMSM正常起動和運行。

內置式PMSM具有凸極性，許多學者基于電機基波模型提出了擴展卡爾曼濾波法[1]、狀態觀測器法[2]等實現轉子初始位置檢測。旋轉高頻電壓注入[3]是通過注入固定幅值的旋轉高頻電壓信號，利用旋轉坐標系變換以及低通和帶通濾波等方法解析電流信號，獲取轉子位置信息[4]。Boussak M等[5-6]使用Clarke變換和擴展卡爾濾波器，解析靜止兩相坐標系電流信號中的轉子位置信息，通過三角恒等式估計轉子位置。文獻[7]通過離散傅里葉解析電機電流信號的直流分量，并采用積分估計器估計轉子位置。但旋轉高頻電壓注入法適用于內置式PMSM。

而表貼式PMSM直軸和交軸電感近似相等，相對于內置式的轉子初始位置檢測難度更高。估計坐標系旋轉高頻電壓注入法[7-8]是表貼式PMSM轉子初始位置檢測研究的熱點。文獻[9]在磁場定向閉環控制系統中注入d軸高頻正弦電壓信號，根據q軸電流信號與轉子位置正比關系，將電流信號通過高通、帶通濾波并積分得出轉子位置估算值。文獻[10]將載波頻率成分法與旋轉高頻電壓注入法相結合，將電流信號濾波、積分，并對載波頻率成分信號解析其飽和分量幅值的正負，實現轉子磁極判別與位置估算。

本文基于PMSM非線性觀測器[12]，通過對表貼式PMSM兩相靜止坐標系下注入高頻電壓信號，實現了表貼式PMSM轉子初始位置快速估計。并應用Lyapunov函數證明了該非線性觀測器的穩定性,對初始位置收斂的象限問題進行了分析。最后的仿真結果證明，與傳統的脈振高頻注入法相比，本方法不需要高通、帶通濾波以及積分, 轉子初始位置收斂快速，易于工程實現。

1 轉子初始位置觀測器

PMSM矢量控制在α，β靜止坐標系下的數學模型：

(1)

式中：R，L，ψf為電阻、電感、磁鏈；iα，iβ，uα，uβ為α，β軸電流電壓；p為微分算子；θe為轉子位置電角度；ωe為轉子電角速度。

設變量：

(2)

觀測變量：

(3)

根據式(1)，可得：

(4)

根據文獻[11]，y非線性觀測器：

(5)

式中:γ>0為非線性觀測器收斂系數。將式(3)代入上式，可得：

(6)

則:

(7)

(8)

證明：

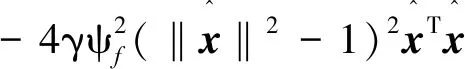
選擇α，β軸高頻注入信號：

(10)

式中：ωh為注入信號的頻率；uA為注入信號的幅值。在高頻注入情況下，觀測變量漸近收斂，穩態點的象限位置由式(6)右邊第一項正負號決定。當PMSM的初始位置為π<θ<1.5π時，觀測變量收斂過程中ωe<0，sinθe<0，cosθe<0，即：

(11)

2 非線性觀測器算法

(f) 循環步驟(c)計算。

3 仿真實驗

PMSM仿真實驗系統參數：4對極，磁鏈0.082 5 Wb，電阻12.4 Ω，電感0.031 9 H，摩擦系數4.8×10-5N·m·s，電機軸轉動慣量1.67×10-5kg·m2，空間矢量PWM頻率10 kHz[12]。非線性觀測器收斂系數8×103，高頻注入信號幅值5 V，頻率500 Hz。

PMSM電角度初始位置為第一象限，注入高頻α，β軸電壓信號，非線性觀測器的觀測變量cosθe，sinθe曲線，如圖1所示。圖1中PMSM電角度初始位置為第一象限0.8rad，觀測變量cosθe，sinθe穩態調節時間為20 ms，收斂快。PMSM非線性觀測器與文獻[9]高頻注入法的初始位置觀測輸出曲線如圖2所示。圖2中，文獻[9]高頻注入法轉子初始位置曲線的穩態調節時間達到80 ms，收斂緩慢。在第一象限，兩種估計方法都無需補償π。

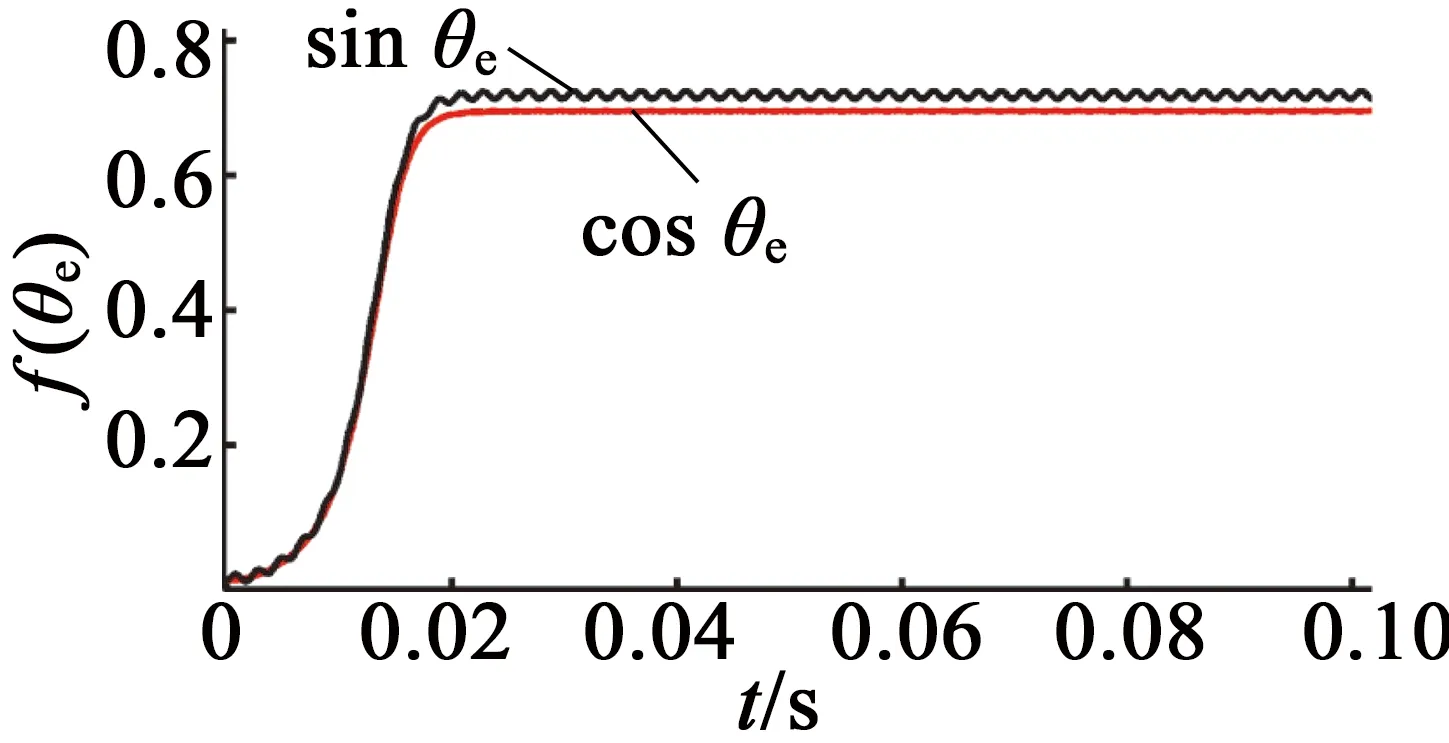
圖1 第一象限非線性觀測器變量曲線

圖2 電機初始位置估計曲線

PMSM電角度初始位置為第二象限，注入高頻信號，非線性觀測器cosθe，sinθe曲線，如圖3所示。圖3中PMSM電角度初始位置為第二象限2.3 rad，觀測變量穩態調節時間短，且cosθe收斂于負數，sinθe收斂于正數，因此高頻注入非線性觀測法無需補償π。非線性觀測器與高頻注入法的初始位置觀測曲線，如圖4所示。圖中文獻[9]高頻注入法除了穩態收斂緩慢，且需要補償π。

圖3 第二象限非線性觀測器變量曲線

圖4 第二象限電機初始位置估計曲線

非線性觀測器與高頻注入法的初始位置在第三、四象限觀測曲線，如圖5、圖6所示。圖5、圖6中，文獻[9]高頻注入法除了穩態收斂緩慢，第三象限需要補償π，第四象限需要補償2π，算法復雜。而高頻注入非線性觀測器法的穩態收斂較快，根據磁極判斷統一補償π。

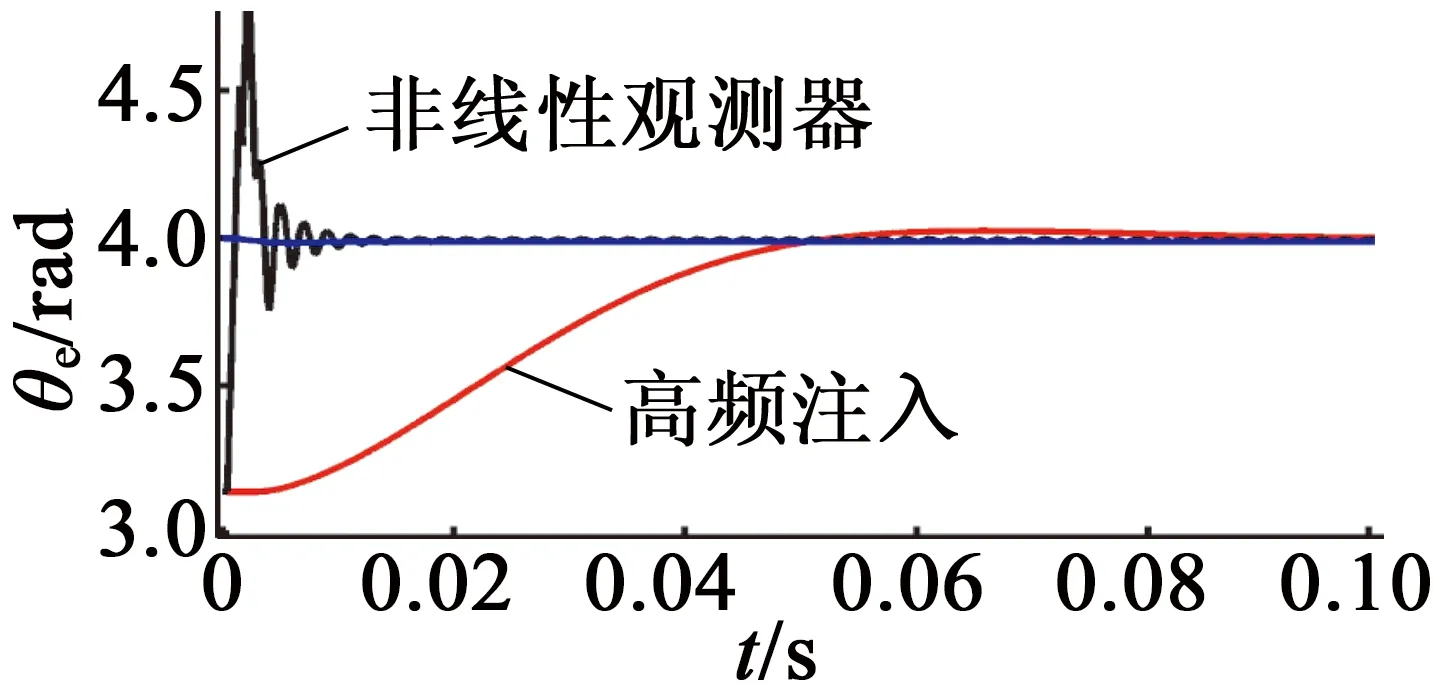
圖5 第三象限電機初始位置估計曲線

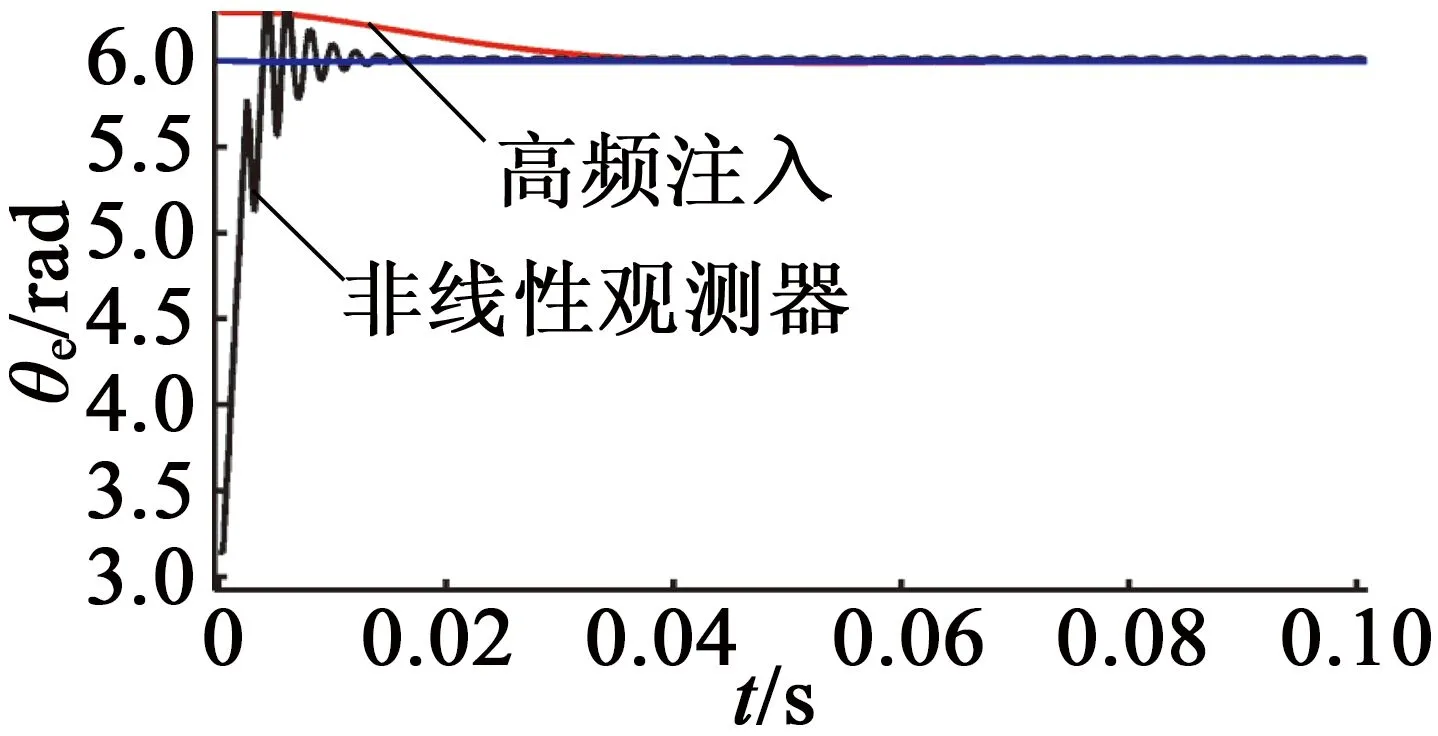
圖6 第四象限電機初始位置估計曲線

4 結 語

本文構建了基于兩相靜止坐標系下注入高頻電壓信號的PMSM轉子初始位置非線性觀測算法，通過Lyapunov函數證明了該觀測器的穩定性。仿真結果表明，本估計方法能夠快速且準確地估計出PMSM轉子初始位置，該方法具有收斂快速、算法簡單等優點，適合工程應用。