打破常規，突破思維方式

吳彬林

【摘要】 在新課程標準下，我們對小學數學的要求已經不僅僅局限于基礎知識的講授，而是更加看重學生對這些知識的應用和對實際問題解決的能力.在解決實際問題的過程中，選擇科學的解題方法，有利于發展學生的思維，提高學習興趣有很大的幫助.小學階段學生一般的“解決問題”思維方式分為順向思維和逆向思維.運用與順向思維相對的逆向思維，要求學生擁有打破思維定式的能力，而這種能力的培養并不是一朝一夕的事情.因此，在小學數學的教學過程中，我們教師應積極鼓勵學生適當運用逆向思維的解題方法應用到解決實際問題當中去，發展學生的思維能力.以下是筆者對小學數學運用逆向思維解決問題小學數學解決實際問題教學方法的一個淺顯地分析.

【關鍵詞】 逆向思維;創新意識;創新能力

綜合法和分析法是小學階段常用解答應用題的方法.所謂綜合法：從已知條件出發，一步一步分析，尋找出要解決的問題的解題方法;分析法：分析法和綜合法的思維正好相反，從問題出發，一步一步分析推算到已知條件思考的方法，也叫逆推法.培養學生運用綜合法和分析法解答應用題習慣叫順向思維和逆向思維的培養.平時的教學過程中發現：一般情況下，絕大部分小學生喜歡運用順向思維解題，只有小部分小學生能運用逆向思維解題.由于小學生的年紀小形象教育為主影響有些數學思想方法他們不易接受.但是我們能聯系學生的思維已有的基礎知識和生活經驗，加強對小學生進行逆向思維的訓練對提高學生思維能力、創新意識和創新能力有極大的幫助.以下是筆者對小學數學運用逆向思維解決問題小學數學解決實際問題教學方法的一個淺顯地分析.

一、循序漸進，從列方程解答過渡到用算術方法解答，培養學生逆向思維的意識

小學數學解決問題一般是通過學生對題目已知條件進行一步一步分析推導，逐步算出答案.分數應用題在小學階段是一個比較難掌握的知識點，相當多小學生在這部分內容學習上感到吃力.教師在教學時應當利用學生原有的知識基礎上幫助學生進行類比區分、歸納總結，發現規律.如“明智幼兒園大班今年有36名小朋友，今年人數比去年人數少了 1 7 ，明智幼兒園大班去年有多少名小朋友？”解題時筆者從引導學生通過自己尋找問題中的等量關系列出方程：x- 1 7 x=36來解答.接著筆者又引導學生通過畫圖、交流后發現：明智幼兒園大班今年有小朋友人數相當于去年人數的 6 7 ，運用逆向思維的方法可以用算術方法列式：36÷ 1- 1 7? .通過這樣教師才能引導學生從順向思維過渡到逆向思維的思考，初步掌握運用逆向思維解決問題的方法.平時訓練要精心設計列方程解答過渡到用算術方法解答進行順向思維和逆向思維訓練同步進行，在設計互逆式問題下點心思，讓學生在實際操作中得到鍛煉.這樣不但可以培養學生養成解法多樣性，還可以打破學生思維中的定式，讓學生的思維一直處于順向和逆向的靈活轉換.列方程解答過渡到用算術方法解答方法既使學生容易掌握基本知識和解題的基本技能，又能逐步培養了學生逆向思維的意識.

二、加強數學知識互逆訓練，培養學生運用逆向思維的方法

聯著名教育心理學家克魯捷茨基曾經提倡培養學生的逆聯想能力.逆想訓練就是要求從小培養學生能根據平時生活中的事例聯想到與之相反或相對立的事例，引發學生進入新的數學意境，產生新的思考.小學數學階段有很多互逆關系的知識：如“乘積是1的兩個數互為倒數”“a×b=c，a和b是c的約數，c是a和b的倍數”“加減法、乘除法是互逆運算”，“判斷成正比例與反比例的兩個量”等等.在平時教學中注重培養學生從正反兩面去思考與理解這些問題，不但可以讓學生容易掌握知識，理解知識的結構，還能培養學生運用逆向思維解決問題的方法.例如，① 2的倒數是（? ）;② （? ）的倒數是 1 7 ;③ 20是（? ）倍數;④ （? ）的倍數是12;⑤ 36千克的 1 3 是（? ）千克;⑥ 30米比（? ）多 1 5 .

三、注重對數學習題的對比訓練，培養學生運用逆向思維的習慣

平時教學中經常出現的現象：有一些題目明明學生已經很好掌握解題方法，并且能夠很快解答出來，但教師把題目稍微改變一下，有部分學生就容易出錯.出現這種情況越是低年級越嚴重.除了年齡特征和知識水平的原因，還有平時教師在日常教學中有沒有對學生注重對數學習題的對比訓練，培養學生運用逆向思維的習慣.如果這種現象不能好好解決會影響學生學習數學的興趣.

教師在講解“解決問題”的時候可以精心設計習題的對比訓練.把一些有代表性的、學生容易混淆的易錯題稍微做一些改編，讓學生訓練后放到一起來講解，讓學生通過對比進行區分，掌握知識的同時也能靈活運用逆向思維解決問題的方法.

如，① 一篇論文有3600字，李老師錄入了這篇論文的 4 9 ，還剩多少字沒有錄入？② 李老師錄入一篇論文，錄入了 5 7 后還剩800字，這篇論文共由多少字？這一組題目乍一看條件都是差不多的，但是仔細觀察就會發現第一道題目的等量關系是不成立的，教師在教學中讓學生自己對比觀察，找出兩道題目中的相同點和不同點.讓學生發現第②題是可以進行逆向思維列算術方法解答，學生解決稍復雜的分數應用題就十分簡單了.因此，注重對數學習題的對比訓練，培養學生運用逆向思維的習慣，對發展學生智力，提高學生學習興趣有很大的幫助.

四、靈活運用數學公式的互逆，培養學生逆向思維的能力

小學數學新授的公式和定律都是通過引導學生猜測并驗證而得到的.一些解題的技巧和靈活性通過猜測并驗證 而得到的，由已知知識逆向思維，一步一步分析推理，最后發現規律后得出計算公式.小學學生一般習慣于從順向思維運用公式解題，沒有養成運用逆向思維解題的習慣和能力.當碰上一些根據公式舉一反三的題目，部分學生容易出錯，而且這種現象長期困擾這部分學生，影響學生學習數學的興趣.因此，在教學中加強對公式的逆運用，引導學生靈活公式的互逆運用，培養學生逆向思維的能力，對提高教學效果有很大的幫助.

如，一個底面積是12平方米，高是6分米圓柱體鐵桶裝滿水，把這些水倒進長24分米，寬8分米，高5分米的長方體容器，這些水會溢出嗎？

解決這道題目的重點理解圓柱的體積等于長方體的體積，圓柱的公式是V=sh，根據公式求出圓柱的體積，但長方體的體積=長×寬×高，需要把公式進行逆運用，長=長方體的體積÷長÷寬或長=長方體的體積÷（長×寬）.求出水裝進長方體容器后的高度，再比較水在圓柱體和長方體高度的大小就可以算出答案.

求周長、面積、體積等是小學數學中常用的公式.公式是解題規律的高度概括，數學中的公式都具有可互逆作用.在教學中加強引導學生運用公式的逆運用，靈活公式的互逆運用，既可以幫助學生對公式的理解和掌握，有可以提高運用公式解決是問題的能力，還可以培養學生的靈活選擇解題方法的思維能力.

五、注意數學問題的逆向轉換，提高學生的創新能力

平時教學中，有些數學問題換個思考方向，把題目又復雜變成簡單.教師要鼓勵學生大膽去創新思考，要從不同角度去思考問題.有時候對一道難題很難弄懂時就要靈活變通注意把數學問題的逆向轉換，會出現“柳暗花明又一村”的效果.所以小學數學教學要注重引導學生靈活變通，注意把數學問題的逆向轉換，有利于學生的逆向思維能力得到提高.

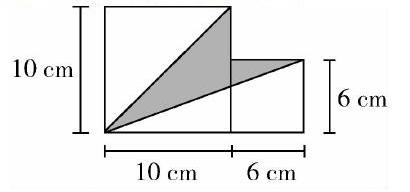
如圖所示，求出陰影部分的面積.

如果從以往的思路入手，找出求陰影部分面積的條件，學生是很難做出來的.假如學生能靈機一動，不去直接求陰影部分的面積，轉過來先求出空白部分面積，然后用總面積減去空白部分的面積就可以求出陰影部分的面積了.

通過教學實踐證明，逆向思維總是與順向思維要交替運用，相輔相成的，數學思維的發展是整體進行的.因此，在日常教育教學中要充分挖掘教材中的互逆內容，加大力度培養學生的逆向思維能力，有助于提高學生思維能力，有助于提高小學生創新意識，有助于提高創新能力.

總之，在小學階段的數學教育是打基礎階段，培養學生的逆向思維能力有助于提高創新能力.萬丈高樓從地起，培養學生的逆向思維要堅持不懈.教師要有計劃、有目的開展逆向思維訓練，只要學生掌握了逆向思維方式，他們的視野更加開闊，思維更活躍，能力得到發展.

【參考文獻】

[1]王琳.小學數學教學中培養學生逆向思維的有效策略[J].學周刊，2015（12）：59.

[2]席振偉.數學的思維方式[J].南京：江蘇教育出版社，1995.