三級供應鏈產品縱向質量管理微分博弈分析

王會會，周溪召 （上海理工大學 管理學院，上海 200093）

0 引言

隨著市場上企業的不斷涌現，消費者在面臨眾多的同類但存在異質性產品時，產品質量便成為首選的關鍵因素。同時，在社會化分工越來越細和產品生產全球化的今天，產品的完成往往需要經過許多廠家進行原料供應、零部件制造加工、商品銷售等過程，這就形成了一條鏈式服務，而產品質量依賴于產品的生產流程及工藝。

鑒于質量管理的重要性，現已經有眾多學者對供應鏈中的產品質量進行了相關研究。Chao[1]提出了如何進行質量改進激勵和產品回購中質量契約設計以解決兩級供應鏈中制造商與供應商質量控制決策；Liu Weihua[2]研究了二級供應鏈中供應商和制造商的質量控制問題；朱立龍[3-4]等基于Stackelberg博弈分析，探討了在靜態情況下三級供應鏈如何制定產品質量控制策略的問題，隨后又基于委托代理理論和博弈論相關理論，研究了生產商和購買商的質量控制契約設計的問題；申強[5]等討論了道德風險下制造商和供應商的質量控制與協調機制；馬鵬[6]等探究了不同公平偏好行為下制造商和零售商的質量投資策略問題；高鵬[7]等分析了不同市場領導結構下二級供應鏈的質量決策問題；洪江濤[8]等運用微分博弈方法研究了兩級供應鏈質量管理過程中博弈結構對均衡結果的影響，張翠華[9]基于質量偏好研究了集成商和提供商所組成的服務供應鏈的質量控制問題；王謙[10]等基于零售商是否共享質量檢測水平信息，研究了非對稱信息下由供應商和零售商構成的兩級供應鏈的質量激勵問題；溫小琴[11]等研究了在中心化供應鏈和由制造商與零售商組成的兩級分散化供應鏈中產品的質量選擇和數量決策；范建昌[12]等研究了制造商CSR對由上游制造商和下游零售商組成的兩階段供應鏈中產品質量、產品需求和利益相關者經濟業績均衡運作結果的影響；趙熒梅[13]等研究了不完全信息下生產企業、經銷商和政府部門對產品質量監管博弈相關問題。以上這些文獻部分運用靜態博弈來研究二級或三級供應鏈質量管理相關問題，部分采用微分博弈的方法，從動態角度分析二級供應鏈質量管理問題，但是基于微分博弈分析三級供應鏈質量管理行為的相關研究十分有限。基于此，本文選擇由一個供應商、一個制造商以及一個零售商組成的三級供應鏈進行分析，建立上下游之間的微分博弈模型，并分析了三種不同決策情況下供應鏈系統的最優利潤和產品質量以及邊際收益對供應鏈系統的行為影響，有利于企業根據實際情況進行合作契約的選擇與制定。

與孫健慧[14]研究進行比較，本文主要有以下不同：（1）其研究的是一個制造商、兩個不同供應商構成的三級裝備制造業供應鏈，而本文在此基礎上引入零售商，研究了由一個供應商、一個制造商和一個零售商構成的一般性供應鏈質量管理問題；（2）其研究假設供應鏈收益與產品質量呈線性函數關系，而本文考慮廣告宣傳，并且假設供應鏈收益依賴于邊際利潤和需求，而需求是由供應商、制造商和零售商及產品質量決定。

1 問題描述與相關假設

1.1 問題描述

1.2 符號說明

Is（t）、Im（t）、Ir（t）：表示t時刻供應商、制造商、零售商在質量管理上的努力程度；

φ1（t ）、φ2（t）：分別表示t時刻供應商和制造商努力成本的補貼比例；

Q（t）：表示t時刻產品的質量，依賴于供應商和制造商的質量管理努力程度，為狀態變量，其中，當t=0時，Q（0）=2；

πs、πm、πr分別為供應商、制造商、零售商的邊際利潤；

Js、Jm、Jr分別表示供應商、制造商以及零售商長期的總利潤。

1.3 模型基本假設

（1）根據參考文獻[15]對質量控制努力成本的假設，供應商和制造商在質量管理上的努力成本分別為Cs（t）=λ 2sI2s（t）和Cm表示供應商和制造商的質量管理努力成本系數；

（2）根據參考文獻[16]對銷售努力成本的假設，本文將零售商在廣告宣傳上的努力成本設為其中 λr＞0，表示零售商廣告宣傳努力成本系數；

（3）單位產品的質量與供應商、制造商的質量管理努力程度相關，具有動態變化的特點，所以假設單位產品質量變化過程的微分方程為其中α和β分別表示供應商和制造商質量管理努力行為對單位產品質量的影響程度；ζ表示外部原因造成產品質量的衰減系數，α、β、ζ＞0；

（4）假設市場需求受產品質量和廣告宣傳努力程度的影響，因此假定需求函數具有如下形式其中D0≥0為常數，表示產品的初始需求，μs、μm、μr分別表示供應商、制造商和零售商的努力行為對產品需求的影響系數，η表示產品質量對產品需求的影響系數，μs、μm、μr、η＞0；

（5）假設供應商、制造商和零售商具有相同的貼現率ρ，ρ＞0，他們的目標都是在無限區間內尋求利潤最大化。

借鑒文獻[17]，假設模型中所有參數都是與時間無關的常數，且博弈在無限時區的任何時段內，參與人面對的是相同的博弈，因此可將策略限制在靜態策略。（為簡化書寫，下文不再列出時間）t

2 分散式決策情形

2.1 Nash非合作博弈情況下

在該情形下，供應商、制造商和零售商各自決策，都追求最大化利潤，用上標N表示。決策過程為：供應商、制造商和零售商三方同時進行決策，此時，他們的決策問題分別為：

結論1：在Nash非合作博弈情況下，供應商、制造商和零售商的最優均衡策略分別為：

證明：參考最優控制[18]的求解方法，可知式均滿足以下HJB方程，即：

分別對式 （7） ～式 （9） 求Is、Im、Ir一階偏導，可得：

將式 （10） ～式 （12） 帶入式 （7） ～式 （9） 得：

根據式（13） ～式（15） 微分方程的特點，推測最優收益函數Vs（Q ）、Vm（Q ）、Vr（Q ）是關于Q的線性解析方程，因而令Vs（Q ）=f1Q+f2,Vm（Q ）=g1Q+g2,Vr（Q ）=h1Q+h2中f1、f2、g1、g2、h1、h2均為常數，并且將其代入式 （13） ～式 （15） 整理可得：

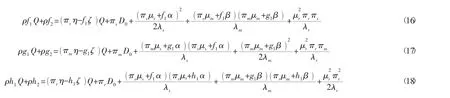
對比式（16）～式（18）左右兩邊的同類項系數，整理可得：

2.2 Stackelberg主從博弈情況下

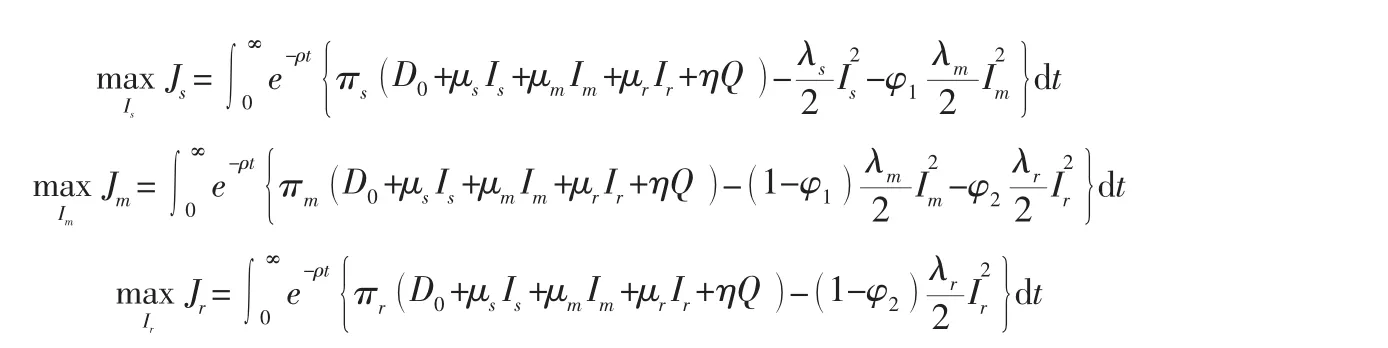
在該情況下，制造商和零售商獨自決策以最大化各自利潤，用下標S表示。決策順序為：供應商、制造商、零售商。此時三方的決策問題為：

結論2：在Stackelberg主從博弈情況下，供應商、制造商和零售商的最優均衡策略分別為：

對式（27） 求Ir一階偏導：

將式 （28） 代入式 （29） 中，可得：

對式（29） 求Im、φ2一階偏導，可得：

將式（28） 和式（30） 代入式（32） 中，并對Is、φ1求一階偏導，可得：

將式 （28）、式 （30）、式 （31）、式 （33）、式 （34） 代入式 （27）、式 （29）、式 （32） 可得：

根據式（35） ～式（37） 微分方程的特點，推測最優收益函數是關于Q的線性解析方程，令Vs其中f1、f2、g1、g2、h1、h2均為常數，并且將其代入式 （35） ～式 （37） 可得：

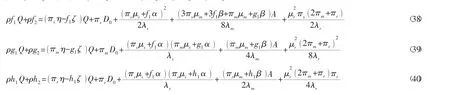
對比式（38）～式（40）左右兩邊的同類項系數，整理可得：

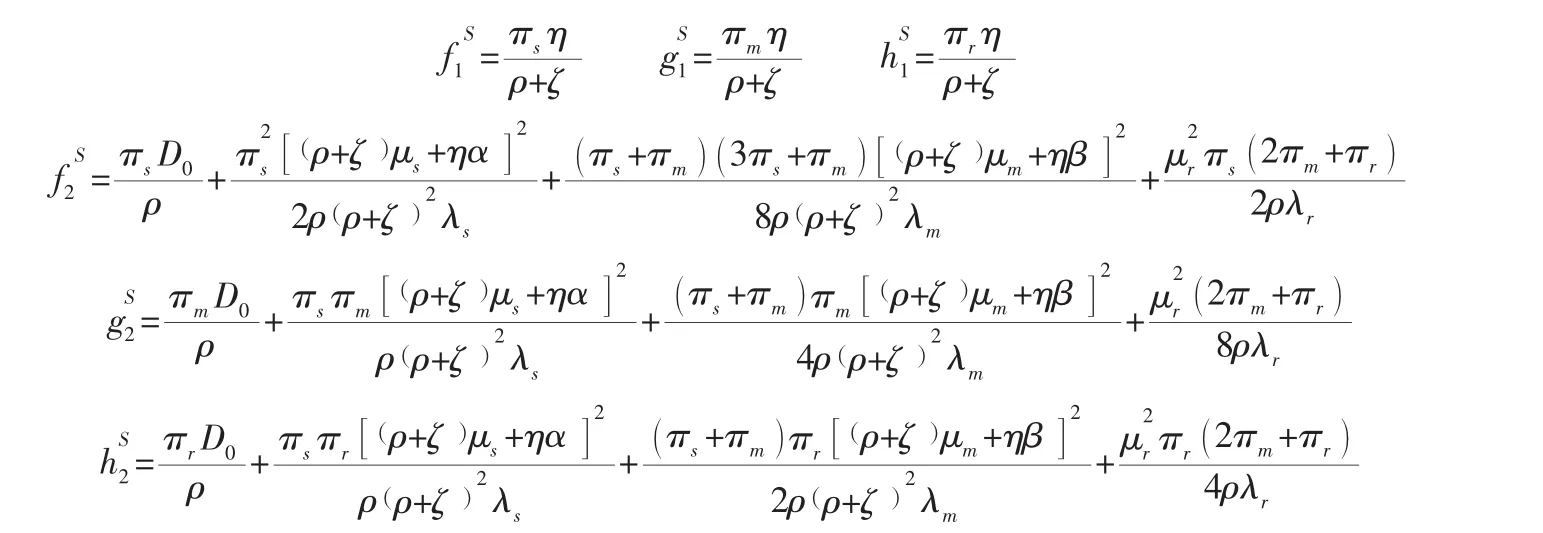
2.3 比較分析

推論1表明，在分散式決策下，供應商的質量管理努力程度在Nash非合作和Stackelberg博弈情形下相同，同時成本分擔比例隨著供應商和制造商的邊際利潤的增加而增加，并且當時，供應商為制造商，制造商為零售商都相應地分擔一定成本，因而制造商和零售商的質量管理努力程度在Stackelberg博弈情形下比Nash非合作博弈下得到加強；當πs≤πm時，供應商和制造商不但不會承擔成本費用，而且會收取一定費用，在一定程度上降低其積極性，因而會造成制造商質量管理和零售商廣告宣傳的努力程度有所下降。

推論2表明，在分散式決策下，由結論2可知，在一定條件下，供應鏈系統（包括供應商、制造商和零售商）的利潤最優值函數在Stackelberg博弈情形下比Nash非合作博弈下實現了Pareto改善。

圖1 兩種決策下供應鏈產品質量和利潤對比

3 算例分析

為了更加直觀地說明供應商、制造商和零售商在分散式決策和集中式決策情況下各自質量管理努力行為和利潤最優水平的變化，可利用數值仿真對上述微分模型進行分析。根據參考文獻[14-15]相關數據取值，具體相關參數設置如下：λs=0.5,λm=0.5,λr=0.4,α=0.4,β=0.3,ζ=0.6,D0=20,μs=0.4,μm=0.6,μr=0.3,η=0.2,ρ=0.1,πs=4,πm=3,πr=4,Q（0 ）=2，其中 πs≥πm將相關參數代入相關結論及推論所給的解析式，借助Matlab R2017a可以給出3種不同博弈情況下供應鏈產品質量和系統總利潤對比關系圖（圖1），供應商、制造商以及零售商分散決策情況下利潤對比關系圖（圖 2）。

圖2 成本分擔前后供應商—制造商—零售商利潤對比

從圖1可看出，3種情況下產品質量和最優利潤情況是：集中式決策情況下最大，無成本分擔時的分散式決策最小，而分散式決策下有成本分擔的Stackelberg主從博弈情況可以達到供應鏈系統利潤的Pareto改善。

供應商、制造商和零售商集中式決策時，供應鏈系統的總利潤及產品質量遠大于兩種分散式決策情況下系統的總利潤，驗證了前面理論推導的結果。集中式決策時供應鏈系統中產品質量增長迅速，而兩種分散式決策情形下產品質量增加緩慢，這充分說明集中式決策優于分散式決策，可以為企業進行優質產品的生產提供參考。

從圖2可以看出，借助有成本分擔的Stackelberg主從博弈可以在一定程度上實現供應商、制造商和零售商利潤的Pareto改善。這是由于供應商分擔了制造商的質量管理成本，而制造商分擔了零售商的廣告宣傳成本，因而最終可以促進零售商大力進行廣告宣傳，從而擴大市場需求，市場需求的增加最終將促進供應商、制造商和零售商利潤的增加，因此使三方的利潤都能達到Pareto改善。

4 結論

本文通過探討由供應商、制造商以及零售商組成的三級供應鏈縱向產品質量管理的動態優化問題，為供應鏈上下游企業獲取最優利潤和生產優質產品提供了相關的理論依據。同時，隨著產品生產企業的不斷涌現以及交易方式的多樣性，產品質量的提升不僅限于縱向供應鏈企業的決策，并且需要考慮橫向競爭，因此，未來可以研究由雙寡頭制造商競爭與合作下的產品質量管理優化問題。此外，文中假設產品的邊際利潤為常量，而實際中，供應鏈節點企業之間的產品交易價格常常是供應鏈運營的決策變量，因此在現有模型中引入批發價格等決策變量，也是我們未來值得研究的問題之一。