構建表格 剖析結構 巧妙獲解*

福建省廈門第一中學 (361003) 王淼生福建教育學院數學研修部 (350025)

張 潔

我們知道數學選擇題的信息不僅體現在題干中，更多隱蔽在選擇支中．要使選擇支中的信息清晰化、簡單化、明了化，一種有效的策略就是列表，通過恰當構建表格將試題信息呈現出來，使得各種條件、關系及內涵一目了然．對于一些復雜問題，列表容易將錯綜復雜關系簡單化，便于我們發現其中的規律，明確解題方向．本文通過三個具體案例來展示這一策略的美妙與實用．

1.三個經典案例

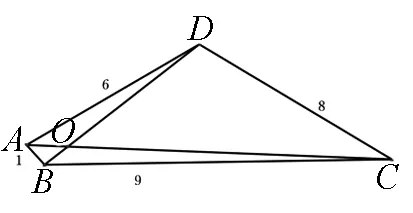
圖1

案例1 四邊形ABCD的邊AB，BC，CD，DA之長分別為1，9，8，6，如圖1所示．對于以下命題：

①四邊形ABCD外切于圓；②四邊形ABCD內接于圓；③對角線不互相垂直；④∠ADC≥90°；⑤ΔBCD是等腰三角形．其中正確的是( ).

A．①真，②假，④真B．③真，④假，⑤真

C．③真，④假，⑤假D．②假，③假，④真

剖析：正常情況下，一般都是從頭到尾直接判斷命題①，②，③，④，⑤的真假性，相當于解答五道試題，這要花費大量的時間與精力，顯然很不合算．對于選擇題，我們當然希望只對其中個別命題加以判斷，并且所判斷的命題個數越少越好．怎樣才能達到這種又快(節約時間)又省(節省精力)又少(命題個數少)呢？這就需要我們對上述選擇支結構予以分析，現將選擇支信息構建如下表格(注：“？”表示未作判斷；“+”表示給予肯定判斷；“—”表示給予否定判斷，下同)：

命題號選擇支 ①②③④⑤A+—?+?B??+—+C??+——D?——+?

觀察上述表格可知，四個選擇支僅僅只對命題④全部作出判斷，因此涉及命題④所透露的信息最多，當然從命題④入手，成為我們破解問題的切入口．由三角形兩邊之和大于第三邊可得ACAC2?∠ADC<90°．因此命題④為假命題，據此否定選擇支A與選擇支D，以下只要對選擇支B與選擇支C加以判斷即可．再觀察上述表格發現：盡管選擇支B與選擇支C，命題③都作出判斷，并且都是給予肯定判斷，因此命題③必然正確．再仔細審視表格發現：只有選擇支B與選擇支C對命題⑤作出了判斷，而且是相反的判斷，其中必有一對，必有一錯，因此從命題⑤下手成為解決問題的關鍵所在．

依據三角形兩邊之和大于第三邊可得：BD

評注：案例1為1986年全國初中數學聯賽試題，距今已有三十多年，是一道經典試題．當年命題專家給出的參考解答就是選取其中三個命題進行判斷，讓人感覺突兀，其實也是盲目的．上述通過構建表格容易發現命題④信息最多，從而否定選擇支A與選擇支D；余下選擇支B與選擇支C，都對命題⑤作出了判斷，而且判斷結果相反，因此必有一對、一錯，于是抓住命題⑤就立即破解案例1．這樣繞過命題①，②，③，尤其避開棘手的命題②，達到不戰而屈人之兵的奇效．

案例2 某校舉行數學競賽，甲、乙、丙、丁、戊五位同學獲得前五名(注：沒有并列名次).發獎前，老師讓他們猜一猜各人的名次.

甲說：乙第三，丙第五；乙說：戊第四，丁第五；丙說：甲第一，戊第四；丁說：丙第一，乙第二；戊說：甲第三，丁第四.

實際上每個名次都有人猜對，則正確的名次是( ).

A.第一名是丙，第二名是乙，第三名是甲，第四名是戊，第五名是丁

B.第一名是丁，第二名是乙，第三名是甲，第四名是戊，第五名是丙

C.第一名是乙，第二名是丙，第三名是甲，第四名是戊，第五名是丁

D.第一名是甲，第二名是乙，第三名是丙，第四名是戊，第五名是丁

名次猜測第一名第二名第三名第四名第五名甲??乙?丙乙???戊丁丙甲??戊?丁丙乙???戊??甲丁?

由上述列表可得，猜第二名的只有乙，依題意“每個名次都有人猜對”從而斷定乙為第二名.由于沒有并列名次，故乙不可能是第三名，由此否定C.以此為突破口，推知甲為第三名，從而否定D.又由表格推知丙為第一名，從而否定B.因此肯定A是正確的，由此得到第一名是丙，第二名是乙，第三名是甲，第四名是戊，第五名是丁.故選A.

評注：案例2為2015年廈門市高三模擬試題.正常情況下都是對選擇支逐個排除.但案例2涉及人數與獲獎名次情況較為復雜，逐個排除顯得非常麻煩.通過列表并將選擇支結構特征進行分析，很快就能確定乙為第二，從而為解決問題尋覓到最佳的切入口.

案例3如果方程|3x|-ax-1=0的解是負數，那么a的取值范圍是( ).

A.a>-3B.a≥3C.a<3D.a≤-3

剖析：為了便于分析，我們將實數集R依據上述選擇支劃分為以下區間并列表如下：

區間選擇支 (-∞,-3)-3(-3,3)3(3,+∞)A??+++B???++C+++??D++???

從上述表格不難看出：選擇支對每個區間信息(判斷)是均等的(每個區間都是2個肯定判斷)，我們無法得到某一個區間上更多信息，怎么辦？如何尋找突破口成為破解問題的關鍵所在.當然從特殊值入手合情合理，即取a=-3時，原方程等價于|3x|+3x-1=0．當x為負數時是得到0=1，顯然該方程無解，與題意矛盾，故應該否定a=-3，也就是說否定選擇支C與選擇支D.對于選擇支A與選擇支B來說，對照上述表格發現：在a=3及a∈(3,+∞) ，都是給予肯定判斷，要么都對，要么都錯，而選擇題必有一個是正確選擇支，否則試題錯誤.注意到選擇支A與選擇支B的包含與從屬關系，如果選擇支A正確，那么選擇支B一定也是正確的，這樣出現兩個正確答案，與題意不符，因此從邏輯上否定選擇支A，故只能是B正確.

評注：案例3為2016年全國初中數學競賽試題，也是文[1]研究的案例.文[1]主要從“方程有負數解，而且只能是負數解”的層面上加以考量.上述解答從選擇支結構特征加以剖析并構建恰當的表格，顯得新穎別致．

2.兩道訓練習題

請讀者模仿上述構建表格的方法并利用結構分析策略來解答以下兩道訓練題：

訓練題1 (2014年廈門一中高三模擬試題改編)一個宿舍住著4名女大學生A，B，C，D，已知她們中有一人在修指甲，一人在做頭發，一人在用早餐，一人在看書．又知道A沒修指甲也沒看書，B不用早餐也沒修指甲，C沒看書也沒用早餐，D沒看書也沒用早餐，試問：大學生A，B，C，D各在做什么？(注：原題為選擇題)

訓練題2 (2007年武漢大學自主招生試題)某珠寶店失竊，甲、乙、丙、丁四人涉嫌被拘審，四人口供如下：

甲：作案是丙；乙：丁是作案者；丙：如果我作案，那么丁是主犯；丁：作案的不是我．

如果四人口供中只有一人是假的，那么以下判斷正確的是( ).

A.說假話的是甲，作案的是乙

B.說假話的是丁，作案的是丙和丁

C.說假話的是乙，作案的是丙

D.說假話的是丙，作案的是丙

(參考答案：訓練題1：A在早餐，B在看書，C在做頭發，D在修指甲，注：本題答案不惟一；訓練題2：答案B)

3.一點心得體會

表格既具有圖形語言的直觀性，又兼有符號語言的簡潔性，更具有文字語言的通俗性，因此是一種值得推廣的方法．構建表格只是一種手段而已，目的是通過列表呈現各類信息，并對信息結構、特征加以分析，從而化難為易、化繁為簡、化隱為顯，其中穿插特值法、邏輯法等多種方法，從而快捷、高效地解決問題．上述這些案例與訓練題，絕大部分都是高考乃至名校自主招生試題，應該說難度較大．借助構建表格，運用剖析結構特征策略，使得問題迎刃而解.