找準切入口 破解隱圓問題有方*

江蘇省南京市第二十九中學高二(4)班 (210036)

劉樂舟 郭建華(指導教師)

在題設條件中沒有直接給出圓方面的信息，而是隱藏在題設條件中，通過題意的深度理解和相關信息整合發現圓(或圓的方程)，從而可以利用圓的相關知識求解，我們稱這類問題為“隱圓”問題.下面就如何尋找解決“隱圓”問題的切入口做一些有益的探索.

類型一 圓的定義

到定點的距離等于定長的點的軌跡叫做圓.

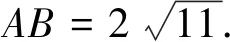
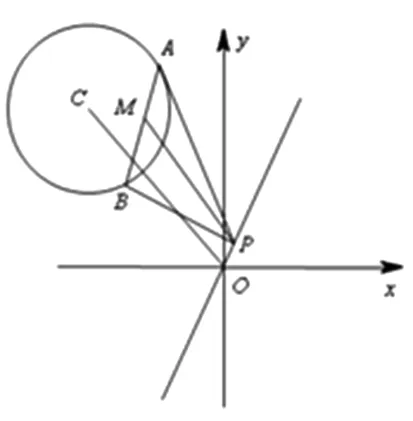
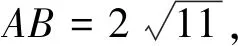
點評:求出線段AB的中點M的軌跡是解決本題的切入口，點M是“無”中生有的，為什么會想到求點M的軌跡呢？由圓C的弦AB為定長，顯然弦AB的中點的軌跡為圓，自然就想到了構造圓，再轉化為方程求解.

類型二 垂直關系圓

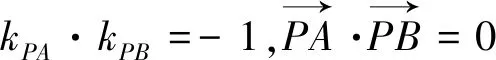
例2 在平面直角坐標系xOy中，直線l1:kx-y+2=0與直線l2:x+ky-2=0相交于點P，則當實數k變化時，點P到直線x-y-4=0的距離的最大值為_________.

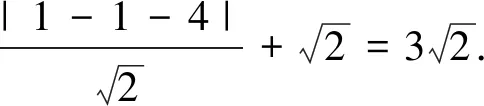
點評:過定點的兩條直線的垂直關系是解題的切入口，解題的關鍵是將垂直的位置關系轉化為數量關系，進而求出點P的軌跡，使問題獲解.

類型三 向量數量積圓

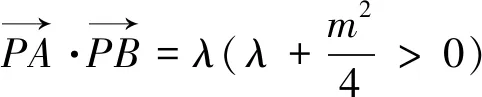
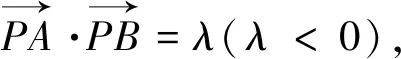
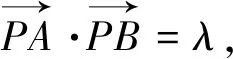
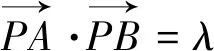
類型四 距離平方圓

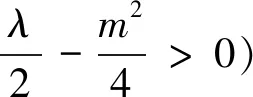
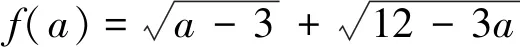
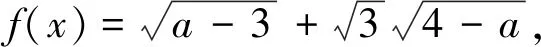
點評:分析無理式函數的結構是解題的切入口，再利用整體換元得到圓的方程，從而將代數問題轉化為幾何問題，結合直線與圓的位置關系進而使問題破解.

類型五 阿波羅尼斯圓

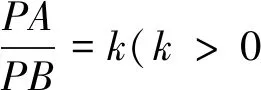
例5 在平面直角坐標系xOy中，點A(0,3)，直線l:y=2x-4，設圓C的半徑為1，圓心在l上.若圓C上存在點M，使MA=2MO，求圓心C的橫坐標a的取值范圍.

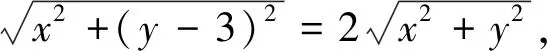
點評:將數量關系MA=2MO，通過“建系、設點、列式、代入、化簡”等步驟得到“阿波羅尼斯圓”是解題的切入口，再結合兩圓的位置關系進而使問題破解.

以上幾個例子都是通過坐標系，充分挖掘題設條件將隱圓問題實現化“隱性”為“顯性”，不愧為培養抽象核心素養的好素材，即在實現“化隱為顯”的過程，找到解決問題最本源的知識和思想方法，從題中的具體背景中抽象出一般的規律和結構，并用數學的語言予以表達，從而深化對概念的理解、掌握、運用，運用數學抽象的思維方式思考并解決問題.