數(shù)學(xué)中也有實(shí)驗(yàn)和創(chuàng)造
——以一節(jié)圓錐曲線的探究課為例

江蘇省揚(yáng)州中學(xué) (225009)

姜衛(wèi)東

1.引言

在一次校際交流活動(dòng)中，筆者要到對(duì)方學(xué)校開設(shè)一節(jié)圓錐曲線的復(fù)習(xí)課.眾所周知，傳統(tǒng)的數(shù)學(xué)復(fù)習(xí)課，無非是這樣的幾個(gè)環(huán)節(jié)：知識(shí)點(diǎn)復(fù)習(xí)→例題精講→課堂檢測(cè)→課外作業(yè).筆者決定打破這個(gè)俗套，來一次復(fù)習(xí)課的創(chuàng)新設(shè)計(jì)，讓學(xué)生感受到數(shù)學(xué)中不僅有概念、公式、定理、證明與計(jì)算，更有大量的實(shí)驗(yàn)與創(chuàng)造！基于這樣的思路，筆者設(shè)計(jì)了一節(jié)有關(guān)圓錐曲線復(fù)習(xí)的探究課.

2.課堂實(shí)錄

2.1 創(chuàng)設(shè)情境 引入課題

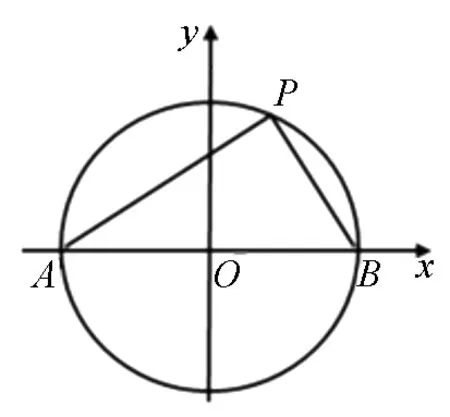
圖1

師：同學(xué)們都知道魯班從野草的葉子聯(lián)想到鋸子.今天，我們就從圓想開去，看看能得到什么成果？首先，請(qǐng)同學(xué)們回憶一下，圓中有哪些性質(zhì)？

生：直徑所對(duì)的圓周角為直角.

師：如圖1，在直角坐標(biāo)系中，若AB為圓O的直徑，則有∠APB=90°,∴kPA.kPB=-1(1).圓中還有哪些性質(zhì)？

生：垂徑定理.

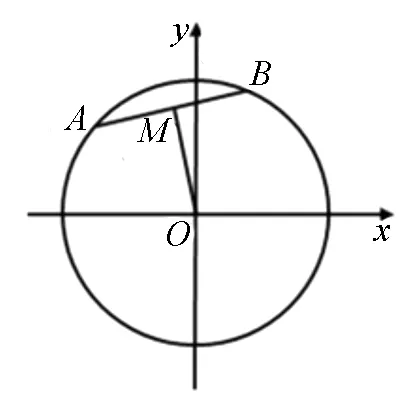
圖2

師：對(duì)！如圖2，在圓O中，若點(diǎn)M為弦AB的中點(diǎn)，則OM⊥AB,∴kOM·kAB=-1(2).

橢圓可以看成是將圓拉伸或壓縮而得到，以上圓中的性質(zhì)(1)與(2)在橢圓及雙曲線中是否也成立呢？接下來，我們一起來開啟探究之旅！

設(shè)計(jì)意圖：圓是學(xué)生熟悉的幾何圖形，初中已研究過它的幾何性質(zhì).在高中解析幾何中，又通過解析法得到了圓的方程，并在此基礎(chǔ)上研究了直線與圓、圓與圓的位置關(guān)系，學(xué)生對(duì)圓的相關(guān)知識(shí)已經(jīng)非常了解，而且在伸壓變換下，圓與橢圓可以進(jìn)行互化，所以這兩種曲線之間存在著一種必然的聯(lián)系.因此，設(shè)計(jì)時(shí)從回憶圓的性質(zhì)出發(fā)，讓學(xué)生進(jìn)行類比聯(lián)想，猜測(cè)橢圓等圓錐曲線的類似性質(zhì).

2.2 問題引導(dǎo) 探究新知

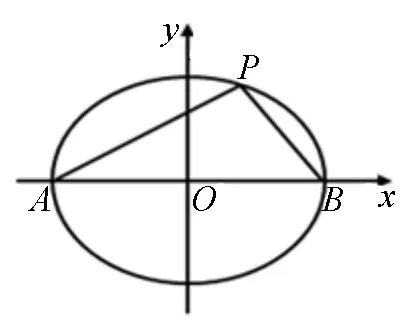
圖3

(學(xué)生經(jīng)過短暫的思考，很快給出了答案)

生：從圖形上直觀判斷，就發(fā)現(xiàn)PA與PB不垂直，這時(shí)kPA·kPB≠-1.

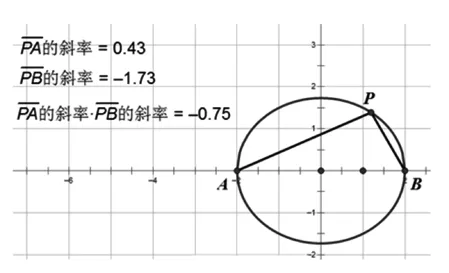
圖4

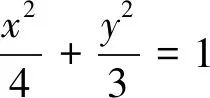
生：應(yīng)該是吧？

師：聽大家的語氣，好像還不太肯定.那么，下面我們就試著進(jìn)行證明，請(qǐng)同學(xué)們自主探究.(學(xué)生經(jīng)過一段時(shí)間的思索，有部分學(xué)生得出了結(jié)論，老師將一個(gè)學(xué)生的過程進(jìn)行投影展示，并適當(dāng)點(diǎn)評(píng))

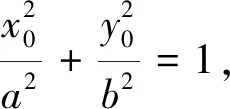
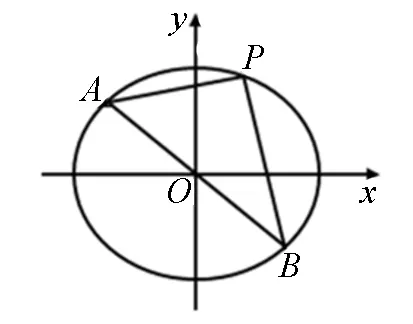
圖5

(一石激起千層浪，學(xué)生一下子活躍起來，有的說是，有的說不是)

師：口說無憑，數(shù)學(xué)中講究嚴(yán)謹(jǐn)性，要么進(jìn)行嚴(yán)格論證，要么舉反例進(jìn)行否定.下面請(qǐng)同學(xué)們分小組進(jìn)行合作學(xué)習(xí)與探究，然后請(qǐng)小組代表發(fā)言.

生：我們小組經(jīng)過證明，發(fā)現(xiàn)結(jié)論仍然成立，理由如下：

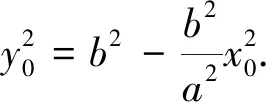
師：前面，我們通過探究，發(fā)現(xiàn)創(chuàng)造了橢圓中的兩個(gè)結(jié)論，它們之間又有什么聯(lián)系？

生：在兩種情況下，A、B這兩個(gè)點(diǎn)都是關(guān)于原點(diǎn)O對(duì)稱的！

師：對(duì)！實(shí)際上，說得更透徹一點(diǎn)，第一種情形可以看成是第二種情形的特例，而第二種情形才更具一般性.以上結(jié)論在橢圓中是成立的，我們?cè)僮鲆淮嗡枷雽?shí)驗(yàn)，類比一下，這個(gè)結(jié)論在雙曲線中是否也成立呢？請(qǐng)同學(xué)們自己寫出問題及結(jié)論.

(提出問題比解決問題更重要！)

圖6

師：這位同學(xué)提出的問題是否正確？我們來進(jìn)行實(shí)驗(yàn).如圖6，在幾何畫板中，拖動(dòng)點(diǎn)P，請(qǐng)同學(xué)們觀察kPA·kPB值的變化情況.

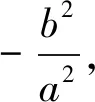
師：根據(jù)前面的探究學(xué)習(xí)，橢圓與雙曲線中kPA·kPB都是定值，但表現(xiàn)形式不同，能否將它們的形式統(tǒng)一起來？

(學(xué)生一下子找不到思路，老師適時(shí)進(jìn)行點(diǎn)撥，引導(dǎo)學(xué)生圓錐曲線中有一個(gè)共同的重要的量，即離心率，從而啟發(fā)學(xué)生將kPA·kPB向e轉(zhuǎn)化)

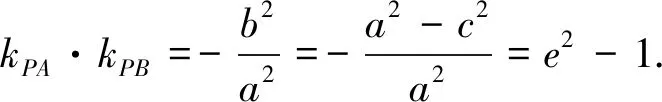
(通過以上的講解，學(xué)生驚訝地發(fā)現(xiàn)，這個(gè)定值居然是統(tǒng)一的.感嘆之余，也讓學(xué)生體悟到數(shù)學(xué)的統(tǒng)一美與簡(jiǎn)潔美！)

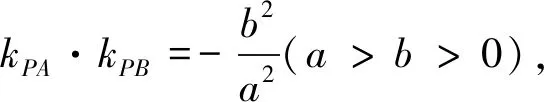
師：關(guān)鍵是看它的軌跡方程是什么？通過方程判斷點(diǎn)P的軌跡是否為橢圓？如何求點(diǎn)P的軌跡方程？

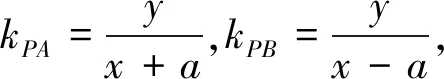
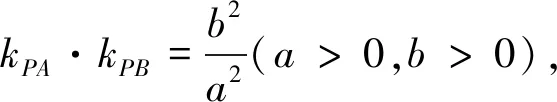
師：下面我們?cè)儆蓤A中的垂徑定理進(jìn)行聯(lián)想、類比和實(shí)驗(yàn).先看橢圓中的情況.同學(xué)們，你會(huì)提出怎樣的問題呢？

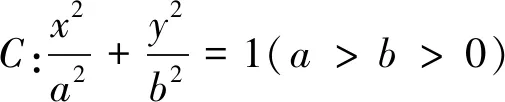
(學(xué)生直覺判斷kOM·kAB應(yīng)該是一個(gè)定值，但不知具體值為多少)

圖7

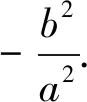
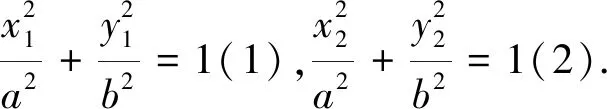
師：還有其它的解法嗎？

生：也可以假設(shè)直線AB的斜率為k,設(shè)出直線AB的方程，利用直線與橢圓的位置關(guān)系及中點(diǎn)坐標(biāo)公式，求出中點(diǎn)M的坐標(biāo)，進(jìn)而表示出直線OM的斜率.

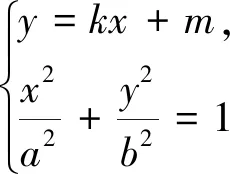
生：也可以直接設(shè)點(diǎn)A,B的坐標(biāo)，求出中點(diǎn)M的坐標(biāo)，表示出kAB·kOM，并利用A,B兩點(diǎn)在橢圓上對(duì)所得式子進(jìn)行化簡(jiǎn).

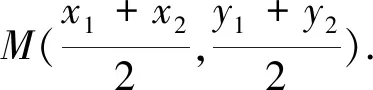
師：同學(xué)們，能否利用前面已經(jīng)得到的結(jié)論來解決這個(gè)問題呢？

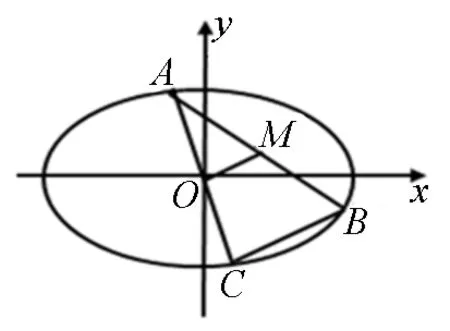
圖8

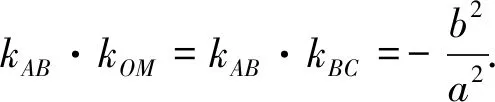
師：太好了！根據(jù)這位同學(xué)的回答，我們發(fā)現(xiàn)上面討論的兩個(gè)問題，在本質(zhì)上是完全一致的！

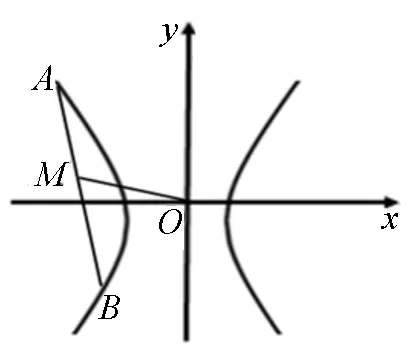
圖9

師：在橢圓與雙曲線中的結(jié)論表面上形式不同，能否將它們統(tǒng)一起來？

(由于類似的問題在前面已探究過，所以學(xué)生不難找到答案)

生：這兩個(gè)結(jié)論可以統(tǒng)一寫成kAB·kOM=e2-1.

設(shè)計(jì)意圖：通過伸壓變換，將圓變化為橢圓后，此時(shí)圓中的兩個(gè)重要的性質(zhì)，即“直徑所對(duì)的圓周角為直角”和“垂徑定理”，在橢圓中已經(jīng)不再成立！那么，又會(huì)是什么性質(zhì)呢？為此，教師組織學(xué)生進(jìn)行實(shí)驗(yàn)，先通過幾何畫板等軟件進(jìn)行動(dòng)態(tài)演示，然后再進(jìn)行思想實(shí)驗(yàn)，即大膽猜測(cè)，最后給出嚴(yán)格的證明.讓學(xué)生經(jīng)歷一次“再發(fā)現(xiàn)，再創(chuàng)造”的過程，這是第一次實(shí)驗(yàn)與創(chuàng)造.在得到橢圓中的相關(guān)結(jié)論后，又進(jìn)行第二次實(shí)驗(yàn)與創(chuàng)造！即大膽地將橢圓中的結(jié)論類推到雙曲線中，通過實(shí)驗(yàn)與嘗試證明，最終發(fā)現(xiàn)這些結(jié)論在雙曲線中也是正確的.不僅如此，在橢圓與雙曲線中的結(jié)論可以完成統(tǒng)一起來，可用同一個(gè)表達(dá)式來表示！接下來，又進(jìn)行第三次實(shí)驗(yàn)與創(chuàng)造，那就是探究上面得到的統(tǒng)一結(jié)論的逆命題是否成立；通過求解動(dòng)點(diǎn)的軌跡方程，利用方程研究曲線的性質(zhì)，得到它的逆命題也是成立的！實(shí)質(zhì)上，這就是橢圓與雙曲線的第三定義.課上到這里，師生并未停下探究的步伐，又進(jìn)行了第四次實(shí)驗(yàn)與創(chuàng)造，通過對(duì)證明過程的辨析，發(fā)現(xiàn)橢圓與雙曲線中得到的這兩個(gè)性質(zhì)在本質(zhì)上又是完全一致的！

3.教后反思

(1)在學(xué)生頭腦中根植一種觀念.在學(xué)生的頭腦中，一直存在著一種偏見和誤解，那就是只有物理、化學(xué)等自然科學(xué)中才存在實(shí)驗(yàn)和創(chuàng)造，在數(shù)學(xué)學(xué)科和數(shù)學(xué)課堂中，無非就是各種定義、法則、公式或定理等等，好像與實(shí)驗(yàn)、創(chuàng)造無關(guān).事實(shí)當(dāng)然并非如此，數(shù)學(xué)中結(jié)論的得來不是空穴來風(fēng)、從天而降，它是通過實(shí)驗(yàn)、創(chuàng)造而來.這里的實(shí)驗(yàn)不僅包含操作類實(shí)驗(yàn)，也包含人的思想實(shí)驗(yàn)，這兩種實(shí)驗(yàn)相互結(jié)合，產(chǎn)生數(shù)學(xué)中的發(fā)現(xiàn)和創(chuàng)造.

(2)教會(huì)學(xué)生一種探究數(shù)學(xué)的方法.新課程理念要求從傳統(tǒng)的接受式教學(xué)向探究式教學(xué)轉(zhuǎn)變.如何進(jìn)行探究式教學(xué)?方法眾多，本節(jié)課向?qū)W生提供了一種探究數(shù)學(xué)的模板，即實(shí)驗(yàn)→猜測(cè)→驗(yàn)證→創(chuàng)造.其中數(shù)學(xué)實(shí)驗(yàn)使學(xué)生提出問題、“發(fā)現(xiàn)數(shù)學(xué)”、“創(chuàng)造數(shù)學(xué)”成為可能.學(xué)生可以通過專門的數(shù)學(xué)軟件進(jìn)行具體的操作演示，發(fā)現(xiàn)其中蘊(yùn)含的數(shù)學(xué)規(guī)律，再通過理性思維進(jìn)行數(shù)學(xué)的抽象概括，形成數(shù)學(xué)的判斷及結(jié)論.當(dāng)然，這些判斷及結(jié)論也不一定正確，還需要進(jìn)行確認(rèn)證明.這就是一條探究數(shù)學(xué)的有效路徑，也是讓學(xué)生從“懂?dāng)?shù)學(xué)”到真正“會(huì)數(shù)學(xué)”的根本轉(zhuǎn)變，更是讓學(xué)生學(xué)會(huì)“數(shù)學(xué)地思維”的必由之路.

(3)培育學(xué)生核心素養(yǎng)的有效路徑.在本節(jié)課中，先通過對(duì)圓中的有關(guān)性質(zhì)類比聯(lián)想，借助合情推理，猜測(cè)橢圓中的相關(guān)結(jié)論，然后進(jìn)行數(shù)學(xué)實(shí)驗(yàn)，直觀感知數(shù)學(xué)結(jié)論的可行性，最后通過邏輯推理確定它的真實(shí)性.在這個(gè)過程中，學(xué)生的直觀想象與邏輯推理得到有效的提升.同時(shí)，在整個(gè)探究教學(xué)的過程中，從圖形中觀察的幾何性質(zhì)上升為數(shù)學(xué)結(jié)論，以及從橢圓推廣到雙曲線等，無一不需要學(xué)生進(jìn)行數(shù)學(xué)抽象與數(shù)學(xué)建構(gòu)，它們的綜合作用也正是培養(yǎng)學(xué)生理性精神、培育學(xué)生數(shù)學(xué)核心素養(yǎng)的有效路徑.

(4)幾點(diǎn)改進(jìn).這節(jié)數(shù)學(xué)探究課是筆者進(jìn)行的一次嘗試，目的在于使學(xué)生認(rèn)識(shí)到數(shù)學(xué)中也有實(shí)驗(yàn)和創(chuàng)造.但在具體實(shí)施教學(xué)的過程中，盡管學(xué)生對(duì)這種教學(xué)形式感到新穎，但筆者也發(fā)現(xiàn)學(xué)生對(duì)這種探究教學(xué)的模式還不太適應(yīng)，對(duì)于如何進(jìn)行數(shù)學(xué)實(shí)驗(yàn)？如何進(jìn)行數(shù)學(xué)創(chuàng)造？學(xué)生有時(shí)會(huì)感到無所適從，不知從哪里入手？實(shí)驗(yàn)與創(chuàng)造的過程中有哪些環(huán)節(jié)？要注意哪些問題等？因此，要真正讓學(xué)生適應(yīng)這種教學(xué)模式，真正掌握并學(xué)會(huì)使用“實(shí)驗(yàn)→猜測(cè)→證明→創(chuàng)造”這種思維模式，還需在今后的教學(xué)中進(jìn)一步強(qiáng)化！