垃圾存儲站選擇問題討論

馬明玥 張萬龍

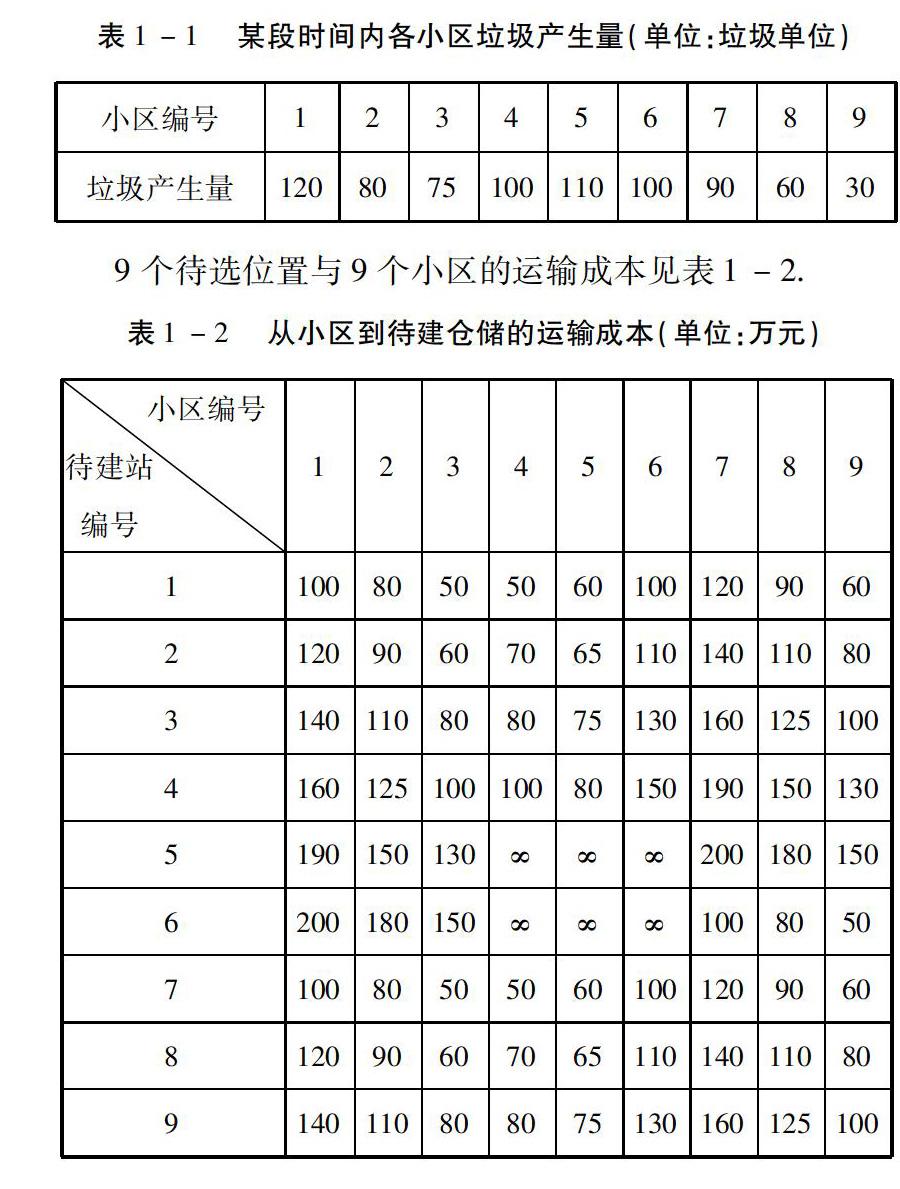
【摘要】本文討論了垃圾存儲站的選址問題，由于要使總的垃圾存處理的花費最小，目標函數是使投資支出與運營成本的總和最低.由于有的垃圾存儲站不需要建設，所以引進了一個0-1變量，由此得到最基本的線性規劃模型，其目標函數為minz=∑9i=1yidi+T∑9i=1∑9j=1cijxij，取T=1，對問題1，其最小費用10 426.2萬元，對問題2，只需要改變小區垃圾保有量用類似可以得到選擇1，5站，最小費用為7 272538萬元.此外，針對垃圾處理站擴容建立了非線性規劃模型.

【關鍵詞】Lingo;垃圾處理;選址;非線性規劃;折舊

一、問題提出

近年來，隨著城市的發展和人口數量的增加，城市的垃圾產量也不斷增加.為了及時處理這些垃圾，減少環境污染，各地小區都在大力推進垃圾處理建設，以便臨時存儲小區的垃圾.9個小區有9個垃圾存儲站位置可供選擇，9個小區某段時間產生的垃圾數量見表1-1.

二、問題分析

（一）問題1的分析

由于不同的小區到不同的垃圾存儲站點的運輸費用不同且不同的站點的建設費用也不相同，那么選擇最優的垃圾存儲站點和制訂正確的垃圾運輸方案就應考慮到運營成本和垃圾站點的使用壽命以及設備折舊的問題.應選在運營成本較低廉，站點使用壽命較長且設備折舊率低的地方.實現建設費與運營費之和最小，并給出垃圾最優運輸方案.

本問題首先采用0-1變量算法得出數學模型，再由數學模型翻譯成Lingo集合語言程序，執行程序后得出決策變量最優值.通過網上調查實際生活中垃圾存儲倉的壽命，得出最優的垃圾存儲選址模型.

（二）問題2的分析

當各小區進行垃圾分類處理，25%的可利用垃圾就不再納入運輸成本中，然后可根據問題1得出的模型，將變動的數據更新在Lingo程序中后計算出垃圾分類后垃圾存儲站建設選擇及運輸方案.

三、模型假設與符號說明

（一）模型假設

假設1：題目中時段長（周期）固定，每周期產生垃圾量不變;

假設2：周期到達小區垃圾清理一次且立刻清空;

假設3：運輸時垃圾可任意分割;

假設4：忽略不可抗力;

假設5：單位容量建設費不變.

【參考文獻】

[1]張萬龍，魏嵬.數學建模方法與案例[M].北京：國防工業出版社，2014.

[2]王正東.數學軟件與數學實驗[M].北京：科學出版社，2009.

[3]姜啟源，謝金星.數學模型（四）[M].北京：高等教育出版社，2016.