函數中的三 類易錯題

胡 玨

有些同學在做函數問題時，感覺做對了，結果卻又做錯了。這主要是由于同學們對概念、性質理解不透導致的。為了幫助同學們更好地掌握這部分內容，下面以例題的形式總結了函數問題中的3類易錯題。

一、概念問題

例1 已知函數y=（m-1）y||m+5m是一次函數，則m的值為（ ）。

A.1 B.-1 C.0或-1 D.1或-1

【錯解】D。

【錯因】忽略一次函數定義中的隱含條件。

【正解】B。

【點評】本題根據一次函數的概念求m的取值范圍時，要考慮兩個方面，一是函數的指數為1，二是該函數的一次項不能為0。同學們很容易忽略第二點。

二、性質運用問題

1.反比例函數中的幾何意義。

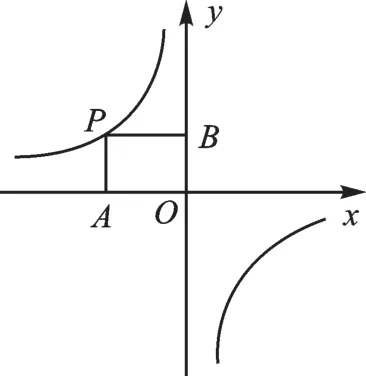
【錯因】錯解知道k的幾何意義，但忽略了圖像的性質。當k＜0時，圖像在第二、四象限。

【點評】本題考查的是k的幾何意義，同學們容易忽視k的值還與圖像的位置有關。

2.二次函數中的平移。

例3 若拋物線y=x2-2x+3不動，將平面直角坐標系先沿水平方向向右平移1個單位長度，再沿豎直方向向上平移3個單位長度，則原拋物線的表達式應變為_______。

【錯解】y=（x-2）2+5。

【錯因】錯解誤將平移平面直角坐標系看作平移拋物線。

【正解】y=x2-1。

【點評】拋物線的平移規律為“左加右減，上加下減”，這個規律的適用范圍是坐標系不動，拋物線平移。本題是拋物線不動，坐標系平移，所以平移規律與上述規律正好相反。

3.函數圖像。

例4 在同一平面直角坐標系中，函數y=ax+b與y=bx2+ax的圖像可能是（ ）。

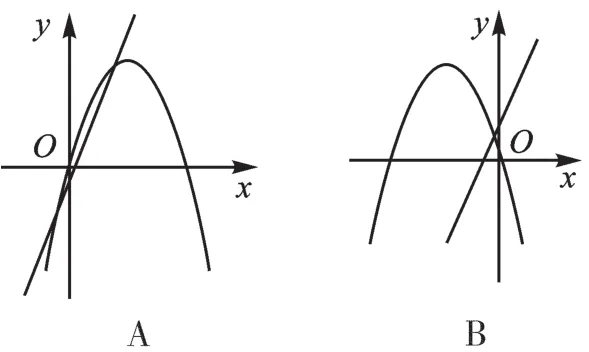
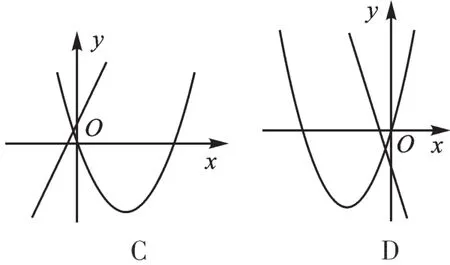
【錯解】B、C或D。

【錯因】遺忘一次函數的圖像性質，難以根據一次函數圖像信息判斷a、b分別與0的大小關系；或者不清楚二次函數的圖像性質，判斷出了拋物線開口方向，卻忽略了頂點位置。

【正解】若a＞0，b＞0，則y=ax+b經過第一、二、三象限，y=bx2+ax開口向上，頂點在y軸左側，故B、C錯誤；若a＜0，b＜0，則y=ax+b經過第二、三、四象限，y=bx2+ax開口向下，頂點在y軸左側，故D錯誤；若a＞0，b＜0，則y=ax+b經過第一、三、四象限，y=bx2+ax開口向下，頂點在y軸右側，故A正確。

【點評】本題考查二次函數與一次函數的圖像，解題的關鍵是明確函數圖像性質，利用分類思想解答。

三、分類問題

1.對“函數”概念的理解。

例5 如果函數y=mx2-6x+2的圖像與x軸只有一個公共點，則m的值為_______。

【錯解】∵y=mx2-6x+2的圖像與x軸只有一個公共點，∴由b2-4ac=0，解得m=。

【錯因】審題不清。題目條件是函數，該函數可以是一次函數，也可以是二次函數。所以要分類討論：如果m=0，函數是一次函數，圖像與x軸只有一個公共點，符合題意；如果m≠0，函數是二次函數，當b2-4ac=0時，頂點在x軸上，也符合只有一個公共點。

【點評】審題時要區分題目中的“函數”“二次函數”“一次函數”等概念性詞語。

2.求函數表達式。

例6 已知一次函數y=kx+b中自變量x的取值范圍是-4≤x≤2，相應的函數值的取值范圍是-5≤y≤7。求此函數的表達式。

【錯解】把x=-4，y=-5；x=2，y=7代入一次函數表達式中，可得{-4k+b=-5，解得{k=2，2k+b=7， b=3，則這個函數的表達式是y=2x+3。

【錯因】x的取值范圍與y取值范圍的對應關系，并不是x與y的對應關系，所以應當有兩種情況。

【正解】（1）當k＞0時，y隨x的增大而增大。x=-4時，y=-5；x=2時，y=7，同上解。（2）當k＜0時，y隨x的增大而減小。x=-4時，y=7；x=2時，y=-5。同理，由待定系數法可得函數表達式為y=-2x-1。綜上所述，這個函數的表達式是y=2x+3或y=-2x-1。

【點評】本題主要考查一次函數的性質。當k＞0時，y隨x的增大而增大；當k＜0時，y隨x的增大而減小。注意要分情況討論。

例7 若一次函數的圖像y=kx+b與兩坐標軸圍成三角形的面積是8，且過點（0，2），求此一次函數的解析式。

【錯解】設一次函數的圖像與x軸、y軸分別交于A、B兩點，則OB=2。∵直線與兩坐標軸圍成的三角形的面積是8，∴×OB×OA=8，

OA=8。∴點A的坐標為（8，0），由待定系數法可得此函數表達式為y=-x+2。

【錯因】當OA=8時，忽視點A的坐標有兩種可能：（8，0）或（-8，0）。

【點評】本題主要考查用待定系數法求一次函數表達式，要分情況討論。