深度學習在初中數學教材解讀中的認識——以《關于原點對稱的點的坐標》課堂教學為例

廣東省廣州市南沙欖核第二中學 江漢標

一、把握教材要有高度

課程標準對教材的定位是“源于教材，但要高于教材”，這是教師在解讀教材、設計教學時必須遵照的準則。教師在解讀教材過程中要做到胸有成竹，要領悟編委對文本編排的意圖，要清晰例題的地位和作用，要明白并處理好習題與例題的關系，還要搞清 “探究、思考、歸納”等教學環節的作用。

例如，本節課教材中設置了“探究”“歸納”“例2”以及“練習”四個學習環節，編委的意圖就是要求學生通過操作——猜想——檢驗的實踐過程，積累數學活動的經驗。直角坐標系中關于原點對稱的點的坐標的關系在學生經歷由具體到抽象地認識問題的過程中通過操作、觀察、歸納得到。從深層次來看，編委要求學生從點坐標與圖形變換的角度揭示中心對稱與軸對稱之間的關系，培養觀察、分析、合作與探究交流的學習習慣，體驗事物的變化之間是有聯系的。所以，筆者事先要求學生采取小組合作的形式對以下內容進行知識儲備及預習：

（1）復習全等三角形的判定及性質；

（2）復習點坐標與長度的關系；

（3）復習在平面直角坐標系中關于坐標軸對稱的點坐標的規律；

（4）探究環節中你能得到哪些結論？與之前所學的知識有哪些關聯？

（5）例2可以有哪些做法？這些做法有什么異同？

當學生完成課前預習環節后，他們對教材內容的認識、對例題的理解以及對本節課的作用與意義就有了初步的認識，這對學生迅速把握課本的核心內容，掌握數學核心思想將起到關鍵的鋪墊作用。

二、處理教材要有廣度

每一個知識點不是孤立的、片面的個體，而是整個知識體系的一環或一點，所以在解讀教材時不能孤立地看待各個數學知識點，而應把它放到整個章節或整個知識系統中去解讀，要善于引導學生把各個知識點放在整體結構中去學習，了解并建立它們之間的關聯與區別。同時還要引導學生建立數學與生活的聯系，體會數學與其他學科的關系，從而擴大學生學習數學的視角，夯實學生深度學習的基礎。

例如，本節課是在前兩節中心對稱的學習基礎上來研究關于原點對稱的點的坐標的規律。由于中心對稱和平移、軸對稱、旋轉一樣，都是全等變換的一種，因此它們不僅在變換與坐標的關系上有很多相似之處，而且在關系的探究視角、方法上也有不少相似之處。所以本節課所運用的探究方式與學生對關于坐標軸對稱的點的坐標的關系的探究方式是一致的，那就是數形結合，先假設后印證。因此，在“探究”環節，筆者是這樣處理的：

（課本P68探究）如圖，在直角坐標系中，作出下列已知點關于原點O的對稱點，并寫出它們的坐標。這些坐標與已知點的坐標有什么關系？

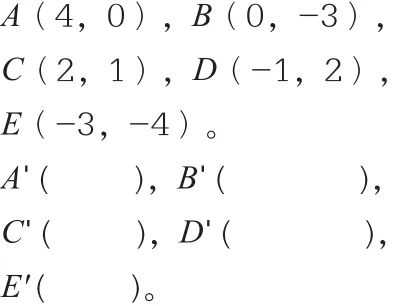
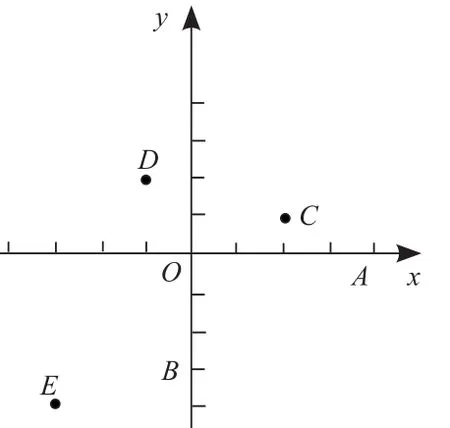
小組討論內容：

（1）兩個對稱點所處的象限有什么關系？

（2）兩個對稱點的橫坐標的符號有什么關系？縱坐標呢？

（3）兩個對稱點的橫坐標的絕對值有什么關系？縱坐標呢？能否以點E為例，用全等知識進行說明？

首先讓學生觀察關于原點對稱的點的坐標之間的特征，然后以小組合作的形式討論老師提出的問題，引導學生從坐標與長度的關系、全等三角形的性質與證明等方面找準本節課的核心內容，最后通過小組匯報總結的形式，讓學生得出它們之間的規律，掌握從特殊到一般的數學思想方法。

三、解讀教材要有深度

解讀教材還要深挖教材，反復鉆研教材上的知識點，細致到每一句話、每一幅圖、每一道題，仔細推敲教材所呈現的數學知識和數學方法，從而領悟編委對教材編排的意圖。

例如，在本節課前，學生已經系統地學習過平移、軸對稱、旋轉、全等、坐標與長度的關系等知識，并能熟練掌握了數形結合的數學思想。所以從教材的編排來看，編委希望教師采用類比教學，根據建構主義，從學生已有的對關于坐標軸對稱的點的坐標的關系的學習基礎上展開教學。

筆者引導學生嘗試用新學規律簡便快捷地畫圖，并結合解題過程讓學生歸納方法，然后精選以下題目：

1.如圖，平行四邊形ABCD的對角線交點在原點O上，已知A點坐標為（-3，2），則C點坐標為（ ）

A.（2，-3）

B.（-3，-2）

C.（3，-2）

D.（3，2）

2.如圖，陰影部分組成的圖案既是關于x軸成軸對稱的圖形，又是關于坐標原點O成中心對稱的圖形。若點A的坐標是（1，3），則點M和點N的坐標分別是（ ）

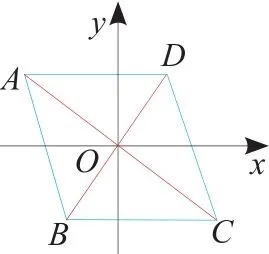
A．M（1，-3），N（-1，-3）

B．M（-1，-3），N（-1，3）

C．M（-1，-3），N（1，-3）

D．M（-1，3），N（1，-3）

3.點P（a，4）關于原點對稱的點Q（3，b），則a+b＝____ 。

4.已 知 點 A（-2，3） 和 點 B（2，-3），則A，B兩個點的位置關系是____________。

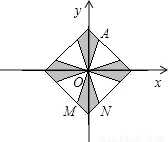
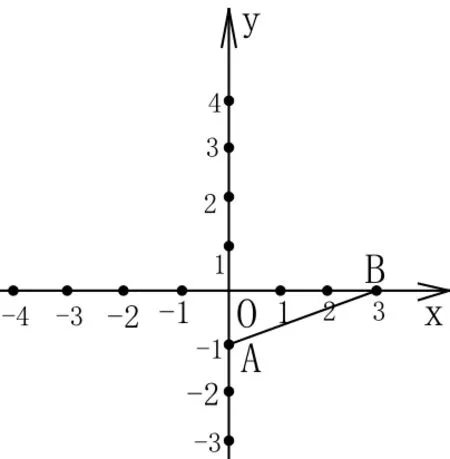
5.如圖，利用關于原點對稱的點的坐標的特點，作出與線段AB關于原點對稱的圖形。

6.在直角坐標系中，將點（-2，3）關于原點的對稱點向左平移2個單位長度得到的點的坐標是（ ）

A.（4，-3）

B.（-4，3）

C.（0，-3）

D.（0，3）

A.1 B.2 C.3 D.4

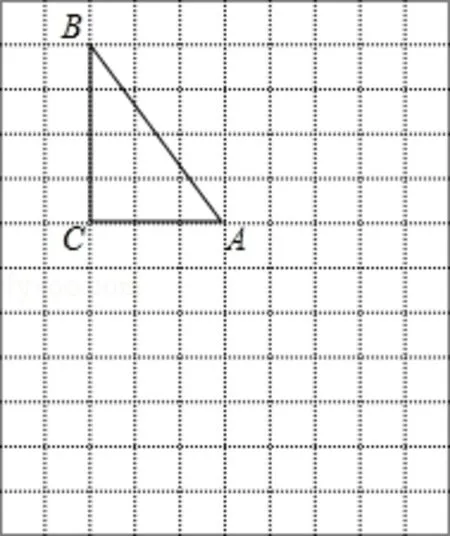
8.在下列網格圖中，每個小正方形的邊長均為1個單位。在Rt△ABC中，∠C=90°，AC=3，BC=4。

（1）試在圖中作出△ABC以A為旋轉中心，沿順時針方向旋轉90°后得到的圖形△AB1C1；

（2）若點B的坐標為（-3，5），試在圖中畫出直角坐標系，并標出A、C兩點的坐標；

（3）根據（2）的坐標系，作出與△ABC關于原點對稱的圖形△A2B2C2，并標出B2、C2兩點的坐標。

通過這樣處理，讓學生在運用新知識的同時，滲透平行四邊形、中心對稱、象限、不等式組、方程組、平移、旋轉、整體代換等內容和方法，讓學生感受各種知識、方法的融合。

解讀教材不是照搬教材，它對教師提出了更高的要求。深度學習需要老師在充分領悟教材意圖的基礎上，立足教材，整合教材內容，深入挖掘教材內涵，對教材進行二次加工，引導學生在更深層次掌握教材的核心內容，把握數學核心思想與方法。同時要注意的是，深度學習不是減少學生的學習任務，更不是降低學生的學習標準，而是對學生的學習提出更高的標準。