翻轉課堂在高中數學教學中的應用

江蘇省如皋中學 張 秦

在課堂上，學生可以采取很多獲取知識的手段來學習，包括看教學視頻、閱讀電子讀物、參加網絡授課、與其他同學交流討論等等。翻轉教學作為大教育運動的一部分，對于促進教育的發展具有重要意義。

一、重視師生互動環節

翻轉課堂教學打破了傳統教育模式的束縛，其更加強調學生作為學習主體的重要性。翻轉課堂開展的形式多種多樣，但是在實際課堂教學過程中，教師應該高度重視師生之間的互動環節。翻轉課堂不意味著學生的學習變得自由散漫，由于中學生的心智尚未成熟，學習過程仍然需要有人督促引導，因此沒有老師引導的翻轉課堂是沒有意義的。在課堂上進行師生互動的方式多種多樣，由于翻轉課堂所采用的學習手段十分廣泛，包括看教學視頻、閱讀電子文件、參加網絡課程、同學們相互交流等，因此師生互動完全不再局限于傳統的提問與回答模式，甚至可以變成一個學習交流會，教師和學生相互分享學習心得，分享在翻轉課堂教學模式下所學到的知識，相互交流在學習過程中遇到的困難，教師要對學生翻轉課堂的學習成果進行鼓勵和肯定，注意對學生學習興趣和自信心的培養。

案例一：在橢圓的學習中，最基本的教學目標是認識橢圓，掌握橢圓的基本概念。在課堂上，教師可以引導學生進行這樣的師生互動：在課堂上做一個有趣的數學實驗，準備一張圓形紙片，將圓心記為O點，讓學生跟著老師講解的步驟一起動手進行操作。在圓形紙片上不同于圓心O的點另取一點記為F，將紙片進行翻折，使得翻折上去的圓弧通過F點，將圓形紙片展開后順著折痕畫上一條直線段，重復上述過程繞圓心一周，看看畫出的圖形是什么？

分析：這是一個課堂上進行的簡單的師生互動活動，運用這個活動進行課題導入，能夠提升學生的興趣，并且學生在進行活動時還能對翻轉課堂自主學習的成果進行檢測，既體現了學生學習的主體性，還使得師生互動環節得以實現。

二、培養自主學習能力

翻轉課堂在高中數學教學中的應用，最主要的就是要培養學生的自主學習能力，因為學生的自主學習能力是整個翻轉課堂能夠有效進行的核心。培養自主學習能力最有效的手段是要充分調動學生的學習積極性，如果學生沒有學習興趣，學習積極性不高，那么培養學生的自主學習能力就是無稽之談。增加學生的學習興趣與提高學生的學習積極性可以從兩個方面進行：第一是彰顯教師的人格魅力，第二是體現教師幽默的教學風格。此外，教師應該對學生的自主學習情況適時進行檢查，因為督促手段對于未成年人的學習來說是十分必要的，自主學習能力的培養要通過平時的教學來體現，在翻轉課堂開始的時候，教師可對學生的課前任務、課后任務進行規劃，對課中的教學重點進行指導，當學生熟悉了這種模式后，自然就投入到自主學習的浪潮中去了。

案例二：已知空間四邊形 ABCD ，E ，F 分別是 AB ，AD 的中點（如圖1）。（1）求證：EF∥平面BCD。（2）找出 EF與平面BCD 內的哪條線平行？

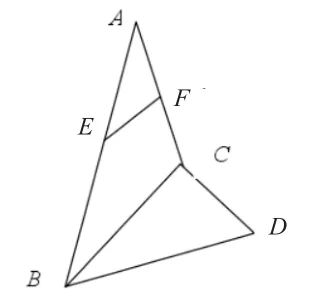
圖1

分析：這是立體幾何開始部分的知識點，教師可以在課前給學生布置這個題目，讓學生進行自主探究，鼓勵他們通過自己的學習在課前解決這個問題，然后根據相應的概念定理寫出詳細的解題證明過程，最后在課堂上更正。學生在課前要解出這個題目，就要對相應的知識點進行學習，包括直線和平面的位置關系、直線與平面平行的判定定理、直線與平面平行的性質定理，這就涵蓋了立體幾何的基礎內容。

三、注重小組合作學習

合作學習在學習中占有重要地位，特別是自新課改浪潮開始以后，合作學習在廣大中小學教學過程中得到大力的倡導，甚至很多學校學生的座位都是按照合作學習的要求來布置的。合作學習能夠有效提高學習效率，不僅如此，合作學習還是學生相互取長補短、相互交流看法、拓展思維的重要機會，特別是有時候一個數學問題的解決方式多種多樣，不同的學生可能擁有不同的方案，進行合作學習能夠促進學生創新意識的產生，對學生的思維能力有較好的培養作用。

案例三：如圖2所示，四棱錐P-ABCD中，底面ABCD為菱形，PA垂直于平面ABCD，BD交AC于E，F是線段PC中點，G為線段AC中點。求證：（1）FG∥平面PBD；（2）BD垂直于FG。

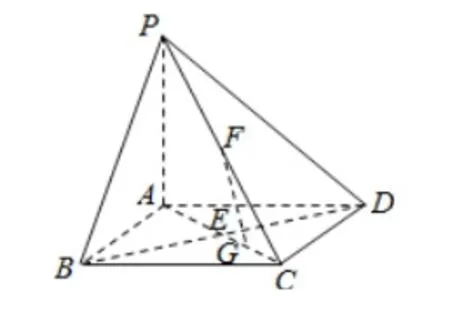
圖2

分析：這是一個典型的立體幾何問題，立體幾何題目的訓練最能夠激發學生的思維能力，對學生的創新能力與邏輯思維都有較好的培養效果。立體幾何問題的解決方式多種多樣，這就需要學生進行合作學習，相互交換意見，而且對于一些比較難的立體幾何問題，合作學習也能夠促進問題的解決。

翻轉課堂是現代教育發展的重要體現，對促進教育教學質量的發展具有重要意義，本文討論翻轉課堂在高中數學教學中的具體應用，主要通過注重師生互動環節、培養自主學習能力、注重合作學習三個方面進行講解，希望對讀者有所幫助。