慣導系統旋轉機構軸承動力學建模方法研究

楊研蒙，姚建軍，閆紅松，袁大義，王永振

(北京自動化控制設備研究所，北京 100074)

0 引言

捷聯慣導是一種十分先進的自主式導航系統。系統的陀螺儀和加速度計直接固連在載體上，去掉了物理機電平臺，用計算機軟件構建了一個數字平臺加以取代。捷聯慣導系統與平臺慣導系統相比，其體積小、質量小且成本低，而系統的可靠性卻大為提高，可以提供更多的導航信息，這給維護和使用都帶來了諸多方便。由于捷聯慣導存在著定位誤差隨時間累積的缺陷，所以在工程實踐中提高慣導系統精度一般有兩種方法[1]:一是提高制造工藝，研制高精度新型慣性敏感器件(Inertial Measurement Unit，IMU)，但系統成本較高；二是通過合理的系統編排，采用誤差補償的方式提高慣性導航精度，這種方法可以以較小的成本投入獲得較大的精度提高。旋轉調制技術就是將現有精度IMU固定在旋轉機構上控制其周期性旋轉，將相應誤差源調制成周期信號形式，從而在導航參數解算過程中得到均化。采用旋轉調制技術與研制高精度慣性器件相比，具有成本低、見效快等特點。但由于旋轉機構軸系的增加導致旋轉調制型捷聯慣導系統結構相對非旋轉調制型捷聯慣導系統結構要復雜得多，因此其結構動力學建模與仿真分析也要復雜得多。

目前，旋轉機構分為單軸旋轉、雙軸旋轉和三軸旋轉三類，其中雙軸旋轉較為普遍。雙軸旋轉調制捷聯慣導系統的旋轉機構，主要由慣性測量組件、外環框架、電機、碼盤、鎖緊裝置、外殼體等部件組成，如圖1所示。其中，慣性測量組件由陀螺、加速度計、電路板等分別緊固在慣性臺體上構成，臺體通過小電機和碼盤內的軸承與外環框架連接；外環框架再通過大電機和另一個碼盤內的軸承與外殼體連接，形成雙軸旋轉系統，該系統在工作時可通過鎖緊裝置來抑制軸系旋轉。

軸承是構成旋轉軸系的關鍵元件，對旋轉機構的運動性能具有重要影響。在系統級動力學仿真中，軸承通常采用等效建模方法。軸承的等效建模方法主要有三種[2-5]：第一種是將軸承看作剛體，不考慮其彈性，這樣做只能在軸承連接關系對結果影響不大且為了節省時間方便計算的條件下使用；第二種是采用彈簧阻尼單元，模擬其軸向自由轉動和徑向線運動剛度；第三種是采用彈簧阻尼單元，模擬其軸向自由轉動、徑向線運動剛度、軸向線運動剛度。在旋轉調制慣導系統的動力學仿真中，這三種建模方法均存在明顯的不足。為此，本文提出了一種同時模擬其軸向自由轉動、徑向線運動剛度、軸向線運動剛度以及徑向角運動剛度的三向剛度等效建模方法。本文研究認為，在動力學仿真中，三向剛度等效建模方法更加符合真實情況。

1 旋轉調制慣導系統旋轉機構軸承建模方法

本文采用ANSYS workbench有限元分析軟件，對旋轉調制捷聯慣導系統旋轉機構進行動力學建模與仿真分析。旋轉機構的軸系均通過雙列深溝球軸承來安裝。深溝球軸承由內外圈和多個滾珠構成，滾珠與內外圈之間通過接觸關系組合在一起，其邊界條件呈非線性狀態。而模態分析一般都是視分析對象為線性變形結構，因此，需要對軸承結構進行一定的簡化處理。

在一般情況下，軸承受徑向力、軸向力和力矩聯合作用時，內外圈將產生徑向軸向相對位移。圖2所示為深溝球軸承在三種不同外載荷的作用下的三種典型振型[6]以及相應的動態參數。

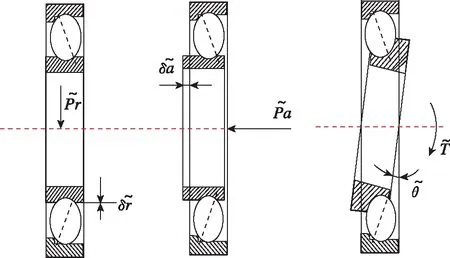
圖2 深溝球軸承三種不同的振型Fig.2 Three different types of vibration ofdeep groove ball bearing

這種彈性的相對位移量對轉軸有著一定的影響，反映了滾動軸承的一種使用性能。通常，用剛度作為衡量此使用性能的指標。所謂滾動軸承的剛度是指軸承內外圈產生的相對彈性位移量所需的外加負載[7]。按照相對位移的方向可以有軸承的徑向剛度、軸向剛度和角剛度等。

在進行動力學性能分析時，軸承部位的建模需要考慮連接處的剛度、質量和阻尼的分布。軸承質量一般作為附加質量分配到定子和轉子上。軸承對阻尼的貢獻加在模態阻尼中，在單元建模時可以不考慮。此次在本文動力學建模中主要詳細模擬其剛度。

軸承剛度的分布可通過給定Bushing單元中剛度矩陣里的K值來模擬。Bushing單元是一種特殊的連接方式，它通過一種數學模型和軟件設置來模擬2個結構間的彈性阻尼連接[8]，一個Bushing單元由6個自由度組成，3個平動自由度：Ux、Uy、Uz和3個轉動自由度：φ、θ、φ，這些自由度可以全部潛在地被定義為自由無約束的旋轉或平動，也可以通過剛度值來抑制這些自由度的運動。Bushing單元由剛度矩陣和阻尼矩陣組成，其中剛度矩陣為

(1)

式中，kx、ky、kz分別代表3個主方向的位移剛度(軸承的徑向剛度和軸向剛度)，kθx、kθy、kθz分別代表3個主方向的轉動剛度(軸承角剛度)。除了對角線上的各項，其余部分都代表各自由度之間的耦合項。

假設Z方向為軸承的軸向，X、Y方向為軸承的徑向，那么旋轉機構在實際工作時，軸承的Z向轉動是無約束狀態的，即kθz=0，且kx、ky為軸承的徑向剛度kr；kθx、kθy為軸承的徑向轉動剛度，因此有kx=ky=kr，kθx=kθy=kθr。耦合項對結果的影響較小，可以忽略不計[9-10]。

最終矩陣式(1)可簡化為

(2)

2 軸承剛度的計算

2.1 滾動軸承剛度的理論計算

軸承的徑向剛度、軸向剛度以及角剛度大小取決于材料、載荷、滾動體、內外圈曲率、接觸角以及加工、裝配等因素。

按文獻[11]，當間隙為0時，單列深溝球軸承受徑向載荷時變形公式為

(3)

(4)

按文獻[12]，當間隙為0時，單列深溝球軸承受軸向載荷時變形公式為

(5)

(6)

而目前關于軸承轉動角剛度的變形公式尚未有文獻可供參考。

式(3)～式(6)中，δr為軸承徑向變形量，μm；δa為軸承軸向變形量，mm；Qmax為承受最大負荷的鋼球上所承受的力，kgf；Q為每個鋼球所承受的軸向負荷值，kgf；db為鋼球直徑，mm；z為鋼球個數；α為初始接觸角，(°)。

滾動軸承的剛度是指軸承內外圈產生的相對彈性位移量所需的外加負載，由于其剛度的變化規律跟很多因素有關，涉及很多非線性關系。因此為了方便計算，定義軸承的剛度為

(7)

式中：F為作用在軸承上的載荷；δ為軸承內外圈所發生的位移量。K值越大，說明軸承的剛度值越大。

由式(3)～式(7)，可以求得深溝球軸承的徑向、軸向剛度表達式為

(8)

(9)

式中，單位為：kgf/mm。

表1所示為本文研究的旋轉機構中代號為618/22HV/P4DB的深溝球軸承的結構參數值。

表1 深溝球軸承參數

將表1數據代入式(8)、式(9)后求得

Kr=1.2×105N/mm

Ka=1.4×105N/mm

2.2 滾動軸承剛度的有限元計算

1)基本假設[13]

1.忽略深溝球軸承徑向游隙和油膜之間的影響；2.忽略軸承保持架和倒角等局部細節；3.軸承內圈和外圈殼保持原來的形狀不變形，只發生剛性位移，即符合剛性套圈假設。

2)軸承有限元分析前處理

定義軸承內外圈和滾動體材質為線彈性材料模型，均使用9cr18鋼，彈性模量E=2×1011Pa，泊松比μ=0.3，材料密度ρ=7700kg/m3。

對軸承部件劃分網格時進行分組均勻網格劃分，對滾動體使用patch conforming method協調分片四面體網格劃分方法。而為了得到更好的收斂結果，對內外圈使用sweep掃略網格劃分，得到全部為六面體的網格單元，如圖3所示，整個模型共361300個節點，138594個單元。

圖3 深溝球軸承有限元模型Fig.3 Finite element model of deep groove ball bearing

由于該軸承為雙列類型，因此滾動軸承中存在四種形式的接觸，即滾動體與內圈、滾動體與外圈、上內圈與下內圈、上外圈與下外圈的接觸，前兩種接觸類型定義為摩擦接觸，摩擦系數為0.02；后兩種接觸類型定義為綁定接觸。

根據軸承的實際工作情況，在計算徑向剛度時，將軸承的內圈內表面全約束，分別在外圈外表面施加Y軸方向的徑向許用載荷3400N和外圈下表面施加X軸方向的軸向許用載荷1750N；在計算角剛度時，對軸承外表面外圈表面全約束，在內圈內表面施加繞X軸方向的力矩載荷3000N·m。

2.3 軸承剛度的仿真結果及分析

圖4、圖6、圖8分別為軸承在受到徑向載荷、軸向載荷、力矩載荷時的整體位移變形圖，為了效果更加直觀，總位移經過一定倍數的放大處理；圖5、圖7和圖9分別為對應的內圈應力分布云圖。從各圖中的應力分布可以看出有限元仿真分析的合理性。

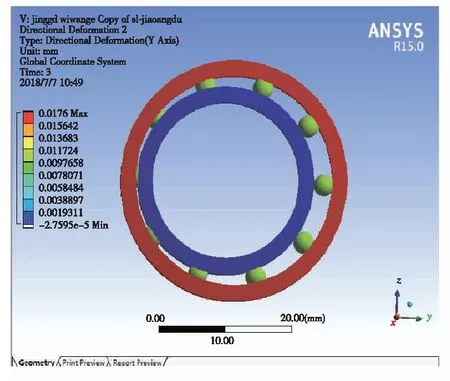
圖4 軸承受徑向載荷時的徑向位移Fig.4 Radial displacement of bearing under radial load

圖5 軸承內圈受徑向載荷時的應力分布Fig.5 Stress distribution of bearinginnerring under radial load

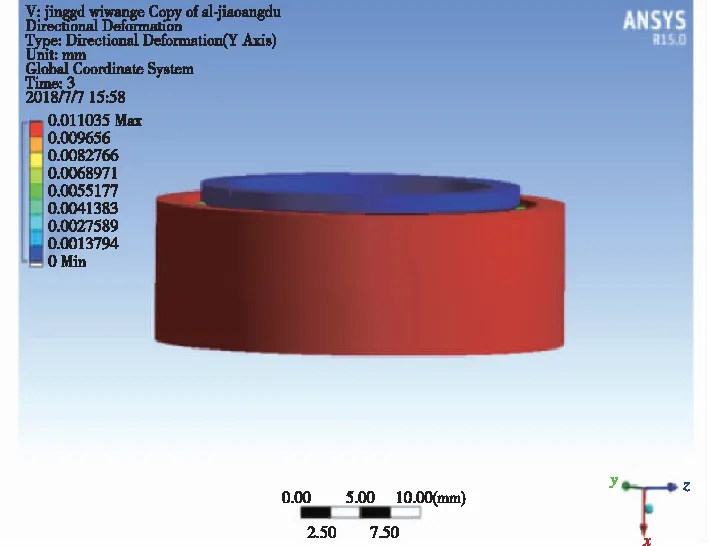
圖6 軸承受軸向載荷時的軸向位移Fig.6 Axial displacement of bearingunder axial load

圖7 軸承內圈受軸向載荷時的應力分布Fig.7 Stress distribution of bearing innerring under axial load

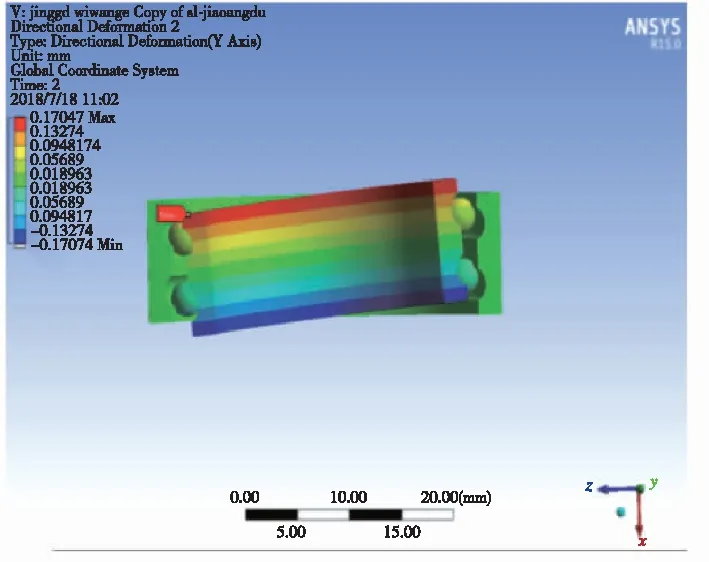
圖8 軸承受轉動載荷時的軸向位移Fig.8 Rotational displacement of a bearingunder rotational load

圖9 軸承內圈受轉動載荷時的應力分布Fig.9 Stress distribution of bearinginner ring under rotational load

再根據式(7)對以上分析得到的數據進行處理計算，得到以下載荷位移曲線圖，如圖10～圖12所示。

圖10 徑向載荷-位移圖Fig.10 Radial load-displacement diagram

圖11 軸向載荷-位移圖Fig.11 Axial load-displacement diagram

圖12 轉動載荷-位移圖Fig.12 Rotational load-displacement diagram

根據曲線圖10～圖12可以看出，在許用載荷的范圍內，隨著外界載荷的增加，軸承的剛度基本為線性的。雖然軸承剛度是變化的，但由于跨度范圍很小，因此考慮選取各點所對應剛度值的平均值進行求解，最后求得該軸承的徑向、軸向和角剛度分別為

Kr=1.91×105N/mm

Ka=1.88×105N/mm

Krθ=1.5×106(N·mm)/(°)

通過驗證式(8)、式(9)得出的軸承徑向和軸向剛度的數值與上文通過有限元仿真分析得到的數值結果在同一量級。由于公式求得的數值為單列球軸承剛度，而文中有限元分析得到的數值為雙列球軸承剛度，在文獻[12]中說明了多列軸承剛度是大于單列軸承剛度的，數據結果也符合此理論依據。因此，證明了本次仿真結果的正確性與有效性。此外，由于經驗公式和擬合公式存在一定的局限性和離散性，而通過有限元仿真分析得到的數值更加精確與具體。所以，軸承剛度的數值最終選擇參考有限元仿真分析所計算出的結果進行處理。

同理，可通過有限元仿真方法計算得到電機與鎖緊裝置里面的相關軸承的剛度。

3 旋轉調制慣導系統旋轉機構的模態分析

模態分析的基本原理[15]：將線性定常系統振動微分方程組中的物理坐標變換為模態坐標，使方程解耦，成為一組以模態坐標及模態參數描述的獨立方程，以便求出系統的模態參數。坐標的變換矩陣為模態矩陣，其每一列為模態振型。由振動理論，系統任一點的響應均可表示為各階模態響應的線性組合。因而，通過求出的各階模態參數就可得到任意激勵下任意位置處的系統響應。模態分析的最終目標是識別出系統的模態參數，為結構系統的振動特性分析、振動故障診斷和預報以及結構力學特性的優化設計提供依據。

在對旋轉機構進行模態分析時，得到了在旋轉機構有、無角剛度時的模態頻率，如表2所示。

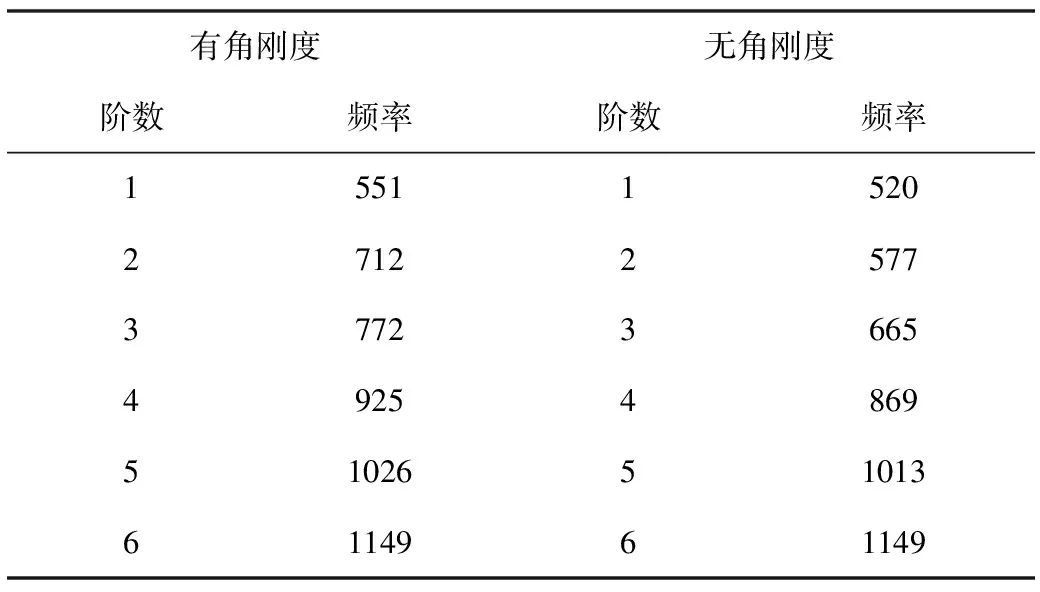
表2 旋轉機構的模態頻率

前五階的振型為：第一階，外環和臺體沿z軸做上下平動；第二階，外環和臺體沿x軸做左右平動；第三階，外環出現對角線方向擠壓變形，臺體受擠壓繞x軸轉動；第四階，外環和臺體繞z軸來回轉動；第五階，外環不動，臺體繞y軸來回轉動。雖然有、無角剛度時，旋轉機構前五階的整體振型都基本相同，但在鎖緊裝置導向柱處的局部振型卻都不相同。例如第一階的局部振型如圖13、圖14所示。可以看出，考慮角剛度時，導向柱處的運動方向和軸承的運動方向相互一致，協調統一；而不考慮角剛度時，導向柱的運動方向與軸承運動方向發生沖突，位移不協調。因此，考慮角剛度時的振型顯得更加真實。

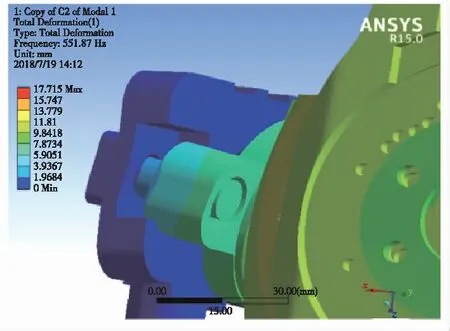
圖13 考慮角剛度時的局部振型Fig.13 Local mode of vibration withconsidering angular stiffness

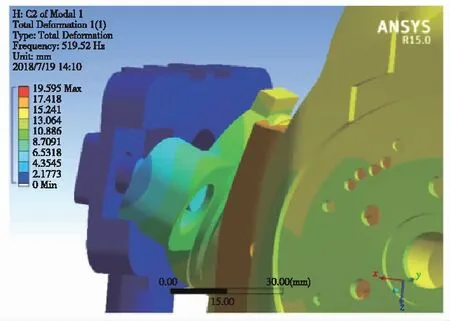
圖14 不考慮角剛度時的局部振型Fig.14 Local mode of vibration withoutconsidering angular stiffness

第六階的振型為外環自身四邊角處的扭轉變形，如圖15所示，由于未和臺體軸承連接處之間發生轉動角位移，因此出現了有、無角剛度時本階模態大小仍一致的情況。

圖15 第六階旋轉機構的振型圖Fig.15 Vibration pattern of the sixthorder rotating mechanism

4 結論

轉動軸系是雙軸旋轉調制捷聯慣導系統的主要結構組成部分，它連接的好壞直接影響到整個系統的動態性能。因此，準確建立各部位連接處的軸承模型，計算其軸承的剛度并代入到整體結構有限元仿真分析所需的參數中將有利于提高結構動力學性能的仿真精度。

本文根據實際情況考慮了計算軸承的角剛度，在進行對比有限元仿真分析后，得出的結果更加貼近真實情況，證實了在對旋轉調制慣導系統裝置進行動力學仿真分析時應當考慮軸承角剛度的合理性。