以理馭法，理法融合——以《螞蟻?zhàn)霾佟返慕虒W(xué)為例

浙江省義烏市香山小學(xué)教育集團(tuán) 陶國(guó)強(qiáng)

計(jì)算教學(xué)是數(shù)學(xué)教學(xué)的重要組成部分，也是小學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)的基礎(chǔ)。在計(jì)算教學(xué)中如何處理算法、算理和算律的關(guān)系值得我們思考與研究。北師大的數(shù)學(xué)教材中，我們發(fā)現(xiàn)在計(jì)算教學(xué)編排中有主講算理的課，如三上乘法《需要多少錢》；理法融合的課，如三下乘法單元的《隊(duì)列表演（二）》；主講算法的課，如四上乘法單元的《衛(wèi)星運(yùn)行時(shí)間》。另外，在有些計(jì)算教學(xué)單元學(xué)習(xí)的安排上也存在這種現(xiàn)象。

《螞蟻?zhàn)霾佟肪褪且还?jié)典型的理法融合的課。在本課的學(xué)習(xí)之前，學(xué)生已較熟練地學(xué)會(huì)了表內(nèi)乘法，并掌握了整十、整百數(shù)及兩位數(shù)乘一位數(shù)的口算方法。并且兩位數(shù)乘一位數(shù)的算理在本冊(cè)教材第四單元中的《需要多少錢》這一課中已經(jīng)學(xué)習(xí)了。本節(jié)課是在學(xué)生學(xué)習(xí)了兩、三位數(shù)乘一位數(shù)的筆算乘法的基礎(chǔ)上，以算理駕馭算法，達(dá)到算理算法相互融合的一節(jié)課，也是今后學(xué)生進(jìn)一步學(xué)習(xí)乘、除法的基礎(chǔ)。下面就以這節(jié)課為例，談?wù)勅绾伍_展理法融合的計(jì)算課教學(xué)。

一、適時(shí)呈現(xiàn)，解釋疑惑

教材中經(jīng)常借助點(diǎn)子圖和列表來(lái)幫助學(xué)生理解計(jì)算的算理和意義。但是如果面對(duì)計(jì)算馬上就提示使用直觀模型不一定會(huì)達(dá)到良好的學(xué)習(xí)效果。有時(shí)“給”得早不如給得“巧”。如《螞蟻?zhàn)霾佟氛n中提出數(shù)學(xué)問(wèn)題，列出算式12×4=之后，讓學(xué)生回顧口算方法。 學(xué)生開始用了橫式計(jì)算：10×4=40，2×4=8，40+8=48，教師引導(dǎo)：還有其他的方法嗎？ 然后再匯報(bào)。

生1：我用的是列表法，把12 分成10 和2，把10 和2 分別寫在表格中，乘號(hào)也寫上，4×10=40，40 就 寫 在10 下 面，2×4=8，8寫在2 下面這一行中，最后40+8=48。

生2：我是用畫點(diǎn)子圖的方法，把點(diǎn)子圖上下分成相同的兩部分，上面部分有2 行，每行12 個(gè)，就是12×2=24，下面的也一樣，24+24=48。

生3：我也是用畫點(diǎn)子圖的方法，我是把點(diǎn)子圖分成左右兩部分，左邊部分是每行10個(gè)，有4 行，10×4=40；右邊部分每行2 個(gè)，有這樣的4 行，2×4=8；再把兩部分加起來(lái)，40+8=48。

師：觀察這兩種方法，你更喜歡哪種？

生∶第二種看上去更容易理解，我更喜歡這種。

……

從上面環(huán)節(jié)可以看出，有時(shí)先讓學(xué)生面對(duì)一個(gè)算式，不急著提供支撐算理理解的點(diǎn)子圖或表格，讓學(xué)生聯(lián)系自己以前的數(shù)學(xué)學(xué)習(xí)經(jīng)驗(yàn)來(lái)嘗試解決問(wèn)題，然后再適時(shí)呈現(xiàn)或點(diǎn)撥，這時(shí)學(xué)生意識(shí)到重要性后主動(dòng)借助圖表學(xué)到的和教師現(xiàn)成提供的效果是有區(qū)別的。

二、溝通聯(lián)系，建立聯(lián)結(jié)

數(shù)學(xué)知識(shí)本身相互之間存在著一定的聯(lián)系，相同的知識(shí)呈現(xiàn)的形式也各有不同。數(shù)學(xué)學(xué)習(xí)就是讓學(xué)生把不同形式的相同的知識(shí)給“聯(lián)結(jié)”起來(lái)，建立健全知識(shí)體系。《螞蟻?zhàn)霾佟肥菍W(xué)生第一次接觸乘法豎式計(jì)算，運(yùn)用豎式的計(jì)算過(guò)程對(duì)學(xué)生來(lái)說(shuō)是比較抽象的，尤其是不容易理解豎式中每一步計(jì)算的實(shí)際含義。通過(guò)板書（線段的連接），將點(diǎn)子圖、列表和豎式計(jì)算中的每一步相互對(duì)應(yīng)起來(lái)，溝通列表數(shù)據(jù)、直觀點(diǎn)子圖、抽象豎式三者之間的內(nèi)在聯(lián)系，清晰地呈現(xiàn)出兩位數(shù)乘一位數(shù)的乘法豎式的計(jì)算過(guò)程，建立有效聯(lián)結(jié)。

（課件出示小組合作任務(wù)及要求）讓學(xué)生說(shuō)一說(shuō)豎式計(jì)算每一步的意思。 合作要求：先自己獨(dú)立思考，可以在作業(yè)紙上畫一畫，寫一寫。然后組長(zhǎng)再組織組員進(jìn)行交流，并選派一名組員匯報(bào)。

全班交流，展示成果。

生1：我們小組是結(jié)合圈點(diǎn)子圖的過(guò)程來(lái)說(shuō)豎式每一步意思的。點(diǎn)子圖的每行2 個(gè)，共4 行的這一部分（2×4=8）就是豎式中第一步2×4=8，點(diǎn)子圖中每行10 個(gè)，共4 行的這一部分（10×4=40）就是豎式中第二步10×4=40，最后再計(jì)算40+8=48。

生2：我們小組是結(jié)合列表法理解豎式每一步意思的。列表法中的2×4=8 就是豎式中第一步2×4=8，列表法中的10×4=40 就是豎式第二步10×4=40，最后把40+8=48。

生3：我們是結(jié)合橫式來(lái)理解豎式每一步的意思的。豎式的第一步2×4=8 就是橫式中的2×4=8，第二步10×4=40 就是橫式中的10×4=40，豎式把40 和8 相加就是橫式中的40+8=48。

學(xué)生點(diǎn)評(píng)，教師小結(jié)。

師：你們的回答都很棒，我們?cè)賮?lái)回憶一下他們的發(fā)言，豎式中的2×4=8 這一步，就是點(diǎn)子圖中的每行2 個(gè)，共4 行的這一部分（2×4=8），就是列表法中第二行右邊的2×4=8，也是橫式計(jì)算中的2×4=8，計(jì)算結(jié)果都是8，我們就把8 寫在個(gè)位上。

豎式中再算10×4=40 這一步，就是點(diǎn)子圖中每行10 個(gè)，共4行的這部分（10×4=40），就是列表法中第二行左邊的10×4=40，也是橫式中10×4=40，計(jì)算結(jié)果是40，寫在第二層，我們就把4 寫在十位上，0 寫在個(gè)位上。

豎式最后算的40+8=48 這步，在點(diǎn)子圖中就是兩部分之和，就是列表法中40+8=48，也是橫式中的40+8=48。（教師邊板書，邊連線，邊講解）

師：我們會(huì)發(fā)現(xiàn)原來(lái)以前學(xué)習(xí)的幾種方法和今天學(xué)習(xí)的豎式方法道理都是一樣的，只不過(guò)形式發(fā)生了變化，從以前的“橫”變成“豎”。

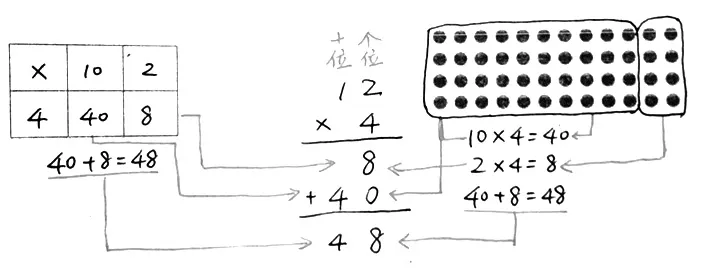
把橫式、列表、點(diǎn)子圖和豎式之間有機(jī)聯(lián)系起來(lái)，讓學(xué)生理解它們之間的關(guān)系，這樣的聯(lián)系觸及了豎式計(jì)算知識(shí)各部分之間的聯(lián)系，使學(xué)生對(duì)豎式計(jì)算的認(rèn)識(shí)與算理思維融會(huì)貫通，對(duì)學(xué)生學(xué)習(xí)豎式計(jì)算有很大的幫助。

三、變化對(duì)比，凸顯結(jié)構(gòu)

在數(shù)學(xué)教學(xué)和學(xué)習(xí)中，變化對(duì)比是一種常用的方法，在對(duì)比中能讓學(xué)生深刻理解和掌握相關(guān)知識(shí)，對(duì)于讓學(xué)生建立正確的知識(shí)體系有重要的意義。本課教學(xué)中，讓學(xué)生通過(guò)觀察不同，進(jìn)行對(duì)比，加深了對(duì)豎式計(jì)算的理解和明確了寫法，促進(jìn)了學(xué)生建構(gòu)清晰的知識(shí)體系。

師：以前的這些算法和豎式計(jì)算有什么不同？（出示思考問(wèn)題）

生1：以前的方法是先算10×4=40，再算2×4=8，最后算40+8=48；豎式計(jì)算是先算2×4=8，再算10×4=40，最后算40+8=48。

師：你觀察得真仔細(xì)。

生2：我發(fā)現(xiàn)豎式計(jì)算比橫式計(jì)算更簡(jiǎn)單，它用豎式把三個(gè)計(jì)算步驟都結(jié)合起來(lái)。

師：豎式是計(jì)算乘法的一種方法。不過(guò)我們用乘法豎式進(jìn)行計(jì)算通常不是像我們剛才那樣寫的，而是這樣寫的（教師板書）。你能看懂嗎？

生1：爸爸以前教我的時(shí)候就是這樣寫的。

生2：這樣寫就是把10 乘4 等于40 直接和8 相加了，最后等于48。

師：這種寫法就是把原來(lái)的加法這一步省略掉了，直接計(jì)算寫出了相加后的答案，這個(gè)算式看上去更加緊湊。

理法融合，抓住了“法”與“理”之間的聯(lián)系，用直觀的“理”來(lái)表達(dá)計(jì)算的“法”，有利于學(xué)生理解每一步的具體含義，有效促進(jìn)對(duì)算理的理解。經(jīng)歷把直觀形象到抽象思考的有效融合過(guò)程。在計(jì)算教學(xué)中做到在學(xué)習(xí)算法中滲透算理的教學(xué)，以理馭法，理法融合是一種行之有效的方法。