數學語言的習得與內化
———《確定位置》教學實錄與反思

王 健

【教學內容】

蘇教版四年級下冊第八單元《確定位置》第一課時。

【教學過程】

一、基于內在需求的認知——“小軍坐在哪里？”

1.提出問題，自主表達。

師：王老師正在給同學們上課，小軍坐在哪里呢？

生：小軍坐在從左往右數的第四組，從下往上數的第三個。

生：小軍坐在第三排第四個。

生：小軍坐在第四組第三個。

生：小軍坐在從右往左數的第三組，從上往下數的第三個。

……

2.反思表達，尋求統一。

師：都在說小軍的位置，為什么你們說的話都不一樣呢？

生：有的是從左往右數第幾組，有的是從右往左數第幾組。

生：有的是先橫著數第幾排，再數第幾個。

生：有的是先豎著數第幾組，再數第幾個。

生：我覺得這樣有點亂。

師：看來，要想說清小軍的位置我們先得統一一下。通常把豎排叫做列，橫排叫做行。一般情況下，確定第幾列要從左往右數，確定第幾行要從前向后數。

師：圖中第一列在哪里？第二列……第一行在哪里？第二行在哪里……

師：現在再看這幅圖，小軍坐在哪里呢？

生：第四列第三行。

【思考：教材中的情境最接近學生的生活經驗，學生在看完圖后直抒胸臆，說的話都在情理之中。說的越不盡相同越能激發學生尋求統一說法的愿望，加上教師引導性的問題，學生的需求更加強烈，此時約定俗成的“列”與“行”就已經不再是生硬地授予，而是一種基于需求的、有意義的接受。】

二、源于主動優化的數學語言習得——“還有更加簡潔的表達方式嗎？”

1.讀示意圖，找小軍的位置。

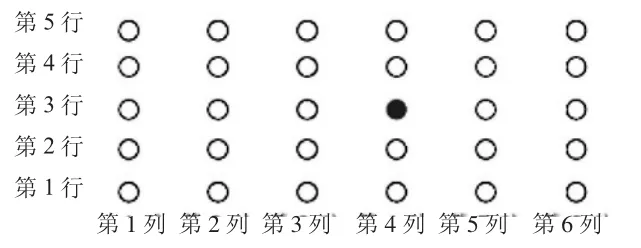
師：如果我們用圓圈表示每位同學的位置，并標上列和行，你能找到小軍的位置嗎？

生：小軍在第四列第三行。（邊說邊在屏幕上有順序地找到小軍的位置）

2.主動優化，自主創造。

（1）自主嘗試，創造更加簡潔的表達。

師：小軍的位置在“第四列第三行”，還有更加簡潔的表達方式嗎？請同學們自己試著寫一寫，在四人小組內交流想法。

（2）匯報交流。

生：我覺得肯定要保留“4”和“3”這兩個數，“4”表示第四列，所以我在旁邊畫了一條豎線，“3”表示第三行，我就畫了一條橫線，我是這樣表示的：4|3—。

生：我沒有用線和箭頭，只是用逗號把4 和3 隔開寫成了“4，3”，左邊的“4”表示第四列，右邊的“3”表示第三行。

生：我覺得寫成“4 3”更簡單一些。

……

（3）達成共識。

師：觀察大家的表示方法，有什么共同之處？

生：都有“4”和“3”這兩個數。

生：這些方法中“4”都表示第四列，“3”都表示第三行。

師：那現在問題又來了，到底該選擇哪種方法呢？

生：我覺得畫線和箭頭還不夠簡潔，直接寫“4，3”更好，反正我們都知道“4”表示第四列，“3”表示第三行。

生：我覺得越簡單越好，但不能寫成“4 3”，這樣會誤會。

師：確實，大家的想法與數學家笛卡爾發明的“數對”不謀而合，我們一起來了解一下。

……

【思考：數學語言的“語法”往往來源于數千年的傳承，抑或是數學家們的首創性表達，這其中的緣由與曲折對于小學生而言，無需過多闡述和解釋。抓住數學表達追求簡明的特質，讓學生從第四列第三行中抽取出“4”和“3”這兩個數，其實就是將學生從被動接受的學習轉變成主動優化的狀態，也就達到了理解數對（4，3）這一數學語言的目的。】

三、應用數對創造特別的座位表——“你會用數對表示你現在的位置嗎？”

1. 觀察自己在班級中的位置，用數對表示。

師：看看我們班的座位，第一列在哪里？第一行呢？

（學生觀察，有困難的學生也可以上臺觀察）

師：你會用數對表示你現在的位置嗎？

生：會。

師：請大家用水彩筆寫在紙條上，然后四人小組交流你們所寫的數對。

2.完成座位表，深度交流。

師：如果這里是講臺，你的位置在哪里？你能把你寫的數對貼上來嗎？

生：我的位置用數對表示是（1，1）。

師：請你們小組的四位同學一起上來，把自己的數對貼在黑板上。

（學生一邊交流一邊貼數對）

師：觀察這四位同學的數對，你有什么發現？

生：佳穎和桐舟都坐在第一列，所以他們的數對中的第一個數都是1。

生：同桌兩人的數對中第二個數都是一樣的。

生：佳穎的位置是（1，1），正宇的位置是（2，2），他們的列和行都相差1。

師：你們真善于發現。還有哪組想上來貼？

……

師：你們還有什么新發現嗎？

生：從（1，1）開始，斜著的一串數對很有意思，（2，2），（3，3），（4，4）……

師：為什么覺得有意思呢？

生：每個數對里的兩個數都一樣。

師：那表示的意思一樣嗎？

生：不一樣。一個表示第幾列，另一個表示第幾行。

生：我覺得這些數對就像是分界線，在分界線的兩邊，每個數對都好像有個雙胞胎兄弟。

師：比如說呢？

生：比如數對（1，2）和數對（2，1）就是一對，如果沿著那條斜線對折，（1，2）和（2，1）就重合了。

師：你的發現真了不起。

……

師：同學們，祝賀你們用數對的知識共同完成了一張我們班的特殊的座位表。這張座位表老師拍下來，課后發布在班級群里，大家還可以繼續尋找其中有意思的地方。

【思考：這個開放性的活動有以下幾點優勢：1.極大地提高了學生主動參與、主動應用的積極性；2.在貼數對時，最先上臺的四位學生要考慮觀測點的問題，在調整時全班的注意力都在這四位學生身上，因為大家都知道如果他們錯了接下來就無法繼續貼了，因此在這個環節，所有學生都明白了確定觀測點的重要性；3.陸陸續續貼了幾組后，規律慢慢顯現出來，學生踴躍地想表達自己的發現，此時學生在解釋自己的發現時都基于數對的本質，即第一個數表示“列”，第二個數表示“行”，即便是兩個數相同但表示的含義也不同，鞏固了對數對的認識；4.面對全班學生用數對共同完成的座位表，學生的成功體驗得到彰顯。】

四、全課總結（略）

【思考：從起初各抒己見的表達，到“列”和“行”的得出；從“第四列第三行”到數對（4，3）；從小軍的座位用數對表示是（4，3）到屬于每位學生自己的數對；從自己的數對到全班的數對座位表。其間，每一位學生都尋求統一、主動優化、交流合作、應用創新。生活化的語言慢慢轉變成了數學語言，陌生的數學語言漸漸內化成了自己的語言。數學學習的魅力就在于此。】