讓學習深度發生
——《確定位置》教學實錄與分析

張 緬

【教學內容】

蘇教版四年級下冊第八單元《確定位置》第一課時。

【教學過程】

片斷一：情境導入，激活創造思維。

1.游戲引入，描述一維空間上任意點的位置。

師：（播放視頻）在一片大森林里，可惡的光頭強又開始亂砍濫伐了。同學們，怎么辦？

生：報警。

畫外音：（警察）各位居民請注意。有誰知道光頭強的具體位置請立刻打電話給我。

根據語音提示在學歷案上用你喜歡的方式畫光頭強的位置。

畫外音：光頭強跑到森林小道最右邊啦！光頭強跑到森林小道正中間啦！光頭強跑到森林小道偏右的地方啦！

師：這次大家怎么找的地方不一樣呢？

生：因為描述的不清楚。

師：那你能清楚地說出光頭強的位置嗎？你可以借助森林里的物體。

生：在第2 根電線桿旁。

師：有不同說法嗎？

生：在第6 根電線桿旁。要明確方向。

師：給電線桿編號是個好辦法。他倆說的都可以，在一條線上按習慣從左往右數。光頭強現在的位置我們用6 來表示。（板書：6）

師：現在呢？（出示光頭強移動到最左邊）你也能用一個數表示嗎？

生：0。

師：這是森林小道的起點，我們用0 表示。（課件顯示并板書：0）

師：（出示光頭強移動到4 和5 之間）現在他的位置呢？也用一個數表示。

生：4.5。（板書：4.5）

師：4.5 是什么數？小數也能表示位置。

師：（出示光頭強移動到3 的位置）現在呢？（板書：3）

師：看來，光頭強只要沿著森林小道跑，我們都能用一個數來表示他的位置。

【分析：游戲是學生喜歡的活動，創設游戲情境，其間不失挑戰性元素，更能激發學生的參與欲。通過游戲回顧了一維空間中點的位置的描述方法。關注0 起點、數的順序，明確直線上任意一點都有唯一的一個數與它對應。為描述二維空間中點的位置打下基礎。】

2.情境激疑，創設平面中任意點造成描述障礙。

師：狡猾的光頭強可沒有那么容易讓你們抓到。接下來他跑到了密林深處。看，光頭強出現了。這個圓點就代表他。他現在的位置誰能說說？

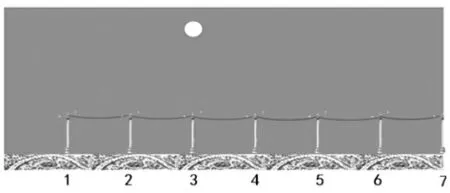
生：3 的前面。

生：3 的正前方。

師：看來，大家都認為光頭強的位置在“3 的正前方”。（板書）

師：你覺得警察憑這樣的線索能準確地找到光頭強嗎？

生：不行。3 的正前方有一條線。

師：上來指指你說的一條線。

師：這條線上無數個點都在3 的正前方是吧？說明信息不夠全面，有點模糊。（教師在“3 的正前方”下面板書“模糊”兩字）

【分析：密林深處的這個點位置如何確定？從確定直線上點的位置到確定平面上點的位置，學生發現用原有方法描述的信息是模糊的，于是形成了認知沖突，促使他們去尋求新的方法。學生的思維水平參差不齊，有的停留在一維水平，有的已經在二維空間考慮這個問題。但課中，不管哪個層次的學生，都圍繞著核心問題努力地思考并尋求問題解決的策略和方法，都不同程度地提高了自己原先對位置表示的理解，優化自身的知識結構。】

片斷二：任務驅動，嘗試自主建構數學知識。

1.實踐操作，自主建構直角坐標系（雛形）。

師：那么，光頭強準確位置的信息該是怎樣的呢？請同學們小組合作研究一下。

合作要求：

（1）獨立思考：想辦法幫警察找到光頭強準確的位置。（可以量一量、畫一畫、標一標）

（2）合作交流：把你的辦法在小組里交流。

生：我量了圓點到森林小道的距離是2 厘米。

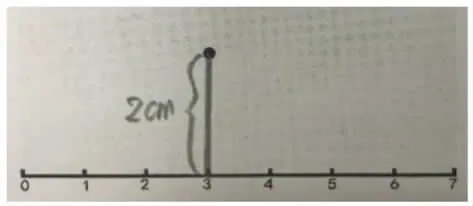
師：光頭強準確的位置在哪？

生：在3 的正前方2 厘米處。（板書：3 的正前方2 厘米處）

生：要是能在圖上豎著放一把尺就好了。

生：我在森林的左邊標上了數字。從光頭強現在的位置對著橫軸和豎軸上相應的數字畫橫線和豎線，這樣看得更清楚。

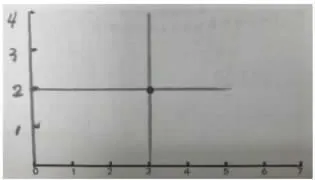
師：要是在6 的上方3 格呢？用你的方法找一找。

生：要是光頭強跑到很多地方，用這樣的方法都能很快找到，在圖上會形成格子。

生：我不僅畫了豎的線，還畫了橫的線，標上刻度。這樣看起來就更方便了。

師：你為什么要這樣畫？

生：豎線為了方便看出光頭強在小路幾的上面，橫線表示離底邊的距離。

師：大家的方法各不相同，但都找到了光頭強的準確位置（在3 的正前方2 格處）。這樣的信息告訴警察你認為怎樣？因為它很——準確（板書“準確”）。

……

【分析：創設了一個開放性的大問題，讓學生自主探索，想辦法確定二維空間里點的位置。由于學生認知起點、思維水平有差異，他們會形成不同層次的思考過程。教師有序地組織學生闡述自己的想法，反思自己的方案，其他學生反駁、爭辯并優化方案。在思維的碰撞中通過集體智慧的共同努力，完成確定位置從一維到二維的突破，逐步創造出平面直角坐標系（第一象限雛形）。這正是本堂課最大的創新點，生動緊湊的互動過程中，有質疑、有補充、有尊重、有完善，成功地實現了“再創造”。】

2.規范約定，用數對表示平面上點的位置。

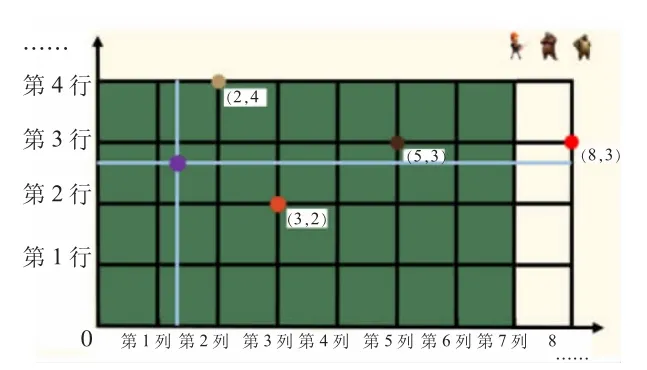
師：老師也學你們用電腦畫畫看。（1）橫豎畫線標刻度；（2）豎線表示列，從左往右分別叫第一列、第二列……以此類推；（3）橫線表示行，從下往上分別叫第一行、第二行……以此類推。光頭強的位置是——

生：第三列第二行。

師：在數學上我們可以用數對表示第三列第二行。［板書：數對。出示（3，2），讀作：數對三二。］數對規定先列后行，它更加簡潔。

師：熊大也來到森林。誰能說說它的位置呢？用數對表示呢？它表示什么？

生：數對（2，3），表示第二列第三行。

師：觀察數對（3，2）和數對（2，3），你有什么想說的？

生：數相同，意義不同；行數和列數相反。

師：你覺得數學家規定數對先列后行有道理嗎？

師：熊二也要來抓光頭強。它的位置在（5，4）。誰能點出它的位置？表示什么？

【分析：在學生理解了數對（3，2）后，巧妙呈現數對（2，3），學生在觀察、對比、說理過程中體會到規定數對有序性的必要以及數對中兩個數各自的含義，更深刻地認識了用有序數對來確定位置的本質。】

片斷三：對比反思，明晰二維描述的核心要素，建立有序數對與平面上任意點的對應關系。

師：回顧剛才的研究過程，你認為確定光頭強在密林深處中的位置和森林小道上的位置有什么不同？

生：森林小道在一條線上，用一個數就可以確定位置；密林深處是一個面，要用兩個數才能確定位置。

師：兩個數能確定平面上所有點的位置嗎？那要是他跑到（8，3）呢？還能找到位置嗎？

生：可以把射線延長。

師：（10，8）呢？（20，30）呢？屏幕外有沒有這樣的位置呢？

師：要是在這個位置呢？

生：把格子畫得再密一點。

生：用兩個小數能表示。

師：在這張坐標圖里可以畫無數條橫線和豎線，看來這樣的方法能快速精確地確定這個平面任何一個點的位置。

【分析：對比確定森林小道和密林深處中點的位置不同之處，其實就是厘清在一維空間與二維空間里確定點的位置的本質。通過這個活動學生進一步明確確定二維空間中點的位置的核心要素是“列”和“行”這兩個信息的有序組合，提升了他們的思維能力和空間想象力。教師創造性地設計了確定網格外部以及單位小格內部點的位置的環節，打開了學生想象的空間，感悟橫軸、縱軸可以無限延長，網線可以無限增加，平面內任意一點都能用有序數對來確定位置。這樣的探究活動，學生不僅學會了用數對確定位置的方法，而且創造性思維、實踐能力也得到發展。】

片斷四：課堂延伸。

師：光頭強見居民們用數對很快就能找準他，于是借助直升機逃跑了，居民們用這樣的數對真的再也找不到他了。聰明的同學們，你知道光頭強逃到哪里了嗎？大家課后可以繼續思考或查閱資料。

【分析：最后創設了一個懸念幫助學生將視野從平面的點拓展到空間中的點，也就是從二維向三維發展。相信有了一維向二維發展時的探究經歷及思維方式作為基礎，他們一定能順利地拓展到三維空間。】